LC諧振電路具有選頻功能,廣泛用于各種通信電路。本文就一階LC電路進行仿真,以此來進一步加深對電路特性的理解和記憶。
諧振
當電路中存在感性元件(如電感)或者容性元件(電容)時,信號源(比如電流源)的頻率變化會使得電路總體呈現容性、感性或者電阻性。當電路呈現電阻性時,就說該電路發生了諧振。最簡單的諧振電路就是一階LC諧振電路,只由一個電感、一個電容和信號源組成。
并聯諧振電路
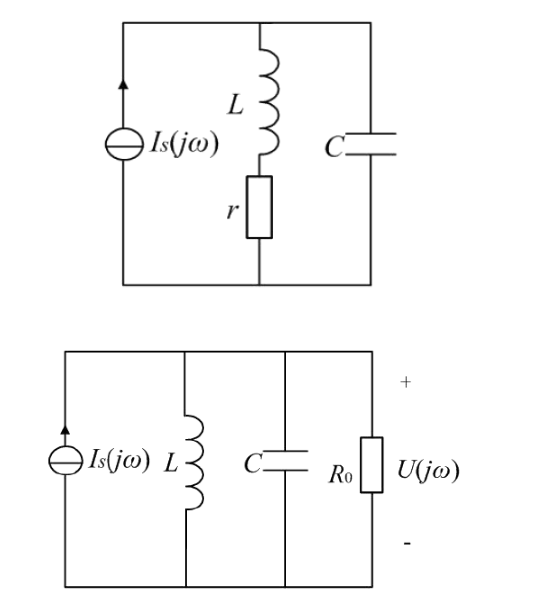
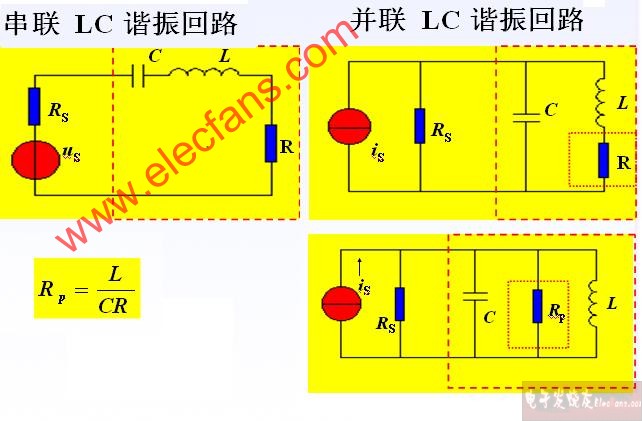
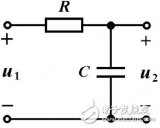
一階并聯型LC諧振電路如上面左圖所示,其中的電阻r是電感的固有損耗,這個固有損耗值一般非常小(以至于理想狀態下可以完全忽略),但是一般進行諧振分析時都把它考慮在內。通常將該網絡等效變換到上面的右圖形式。這個電路有以下幾個重要參數:
1、諧振條件$\omega C = \frac{1}{\omega L}$,滿足該條件的諧振角頻率$\omega_0 = \frac{1}{\sqrt{L C}}$,諧振頻率$f_0=\frac {\omega_0} {2 \pi} $;
1、等效電阻$R(\omega)=\frac{(\omega L)^2}{r}$;
2、發生諧振時,$R(\omega)$記為諧振電阻$R_0$,$R_0=\frac{(\omega_0 L)^2}{r}$;
3、品質因數$Q_0=\frac{R_0}{\omega_0 L}=R_0 \omega_0 C$;
4、通頻帶$B_0.7=\frac{f_0}{Q_0}$;
串聯諧振電路
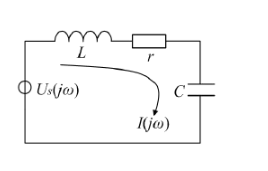
串聯諧振電路的很多公式跟并聯是相似的,有些特性與并聯也是對應的。串聯回路的分析要簡單很多,可以很容易寫出阻抗表達式。而且也不用進行等效變換,該電路的一些公式結論如下:
1、諧振條件為$\omega L = \frac{1}{\omega C}$,諧振角頻率不變,仍然是$\omega_0 = \frac{1}{\sqrt{L C}}$,諧振頻率$f_0=\frac {\omega_0} {2 \pi} $。
2、因為電阻r直接作為了阻抗的實部,因此諧振電阻$R_0=r$。
3、品質因數是并聯的倒數,$Q_0=\frac{\omega_0 L}{R_0}=\frac{1}{R_0 \omega_0 C}$。
4、通頻帶$B_0.7=\frac{f_0}{Q_0}$;
諧振電路仿真
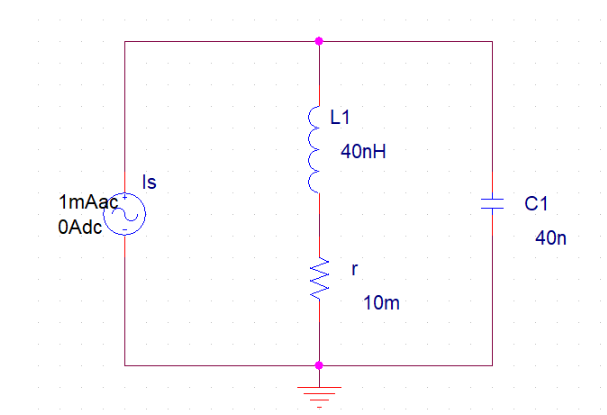
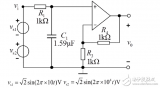
以并聯電路為例,在PSpice中連接好最基本的電路,電路參數在圖中已經標明。根據第一節的結論公式和該并聯電路器件參數,我們可以計算出電路的諧振角頻率、諧振頻率、諧振電阻、品質因素分別為:$\omega_0=25M rad/s$、$f_0 \approx 3.9789MHz$、$R_0=100 \Omega$、$Q_0=100$。
阻抗特性
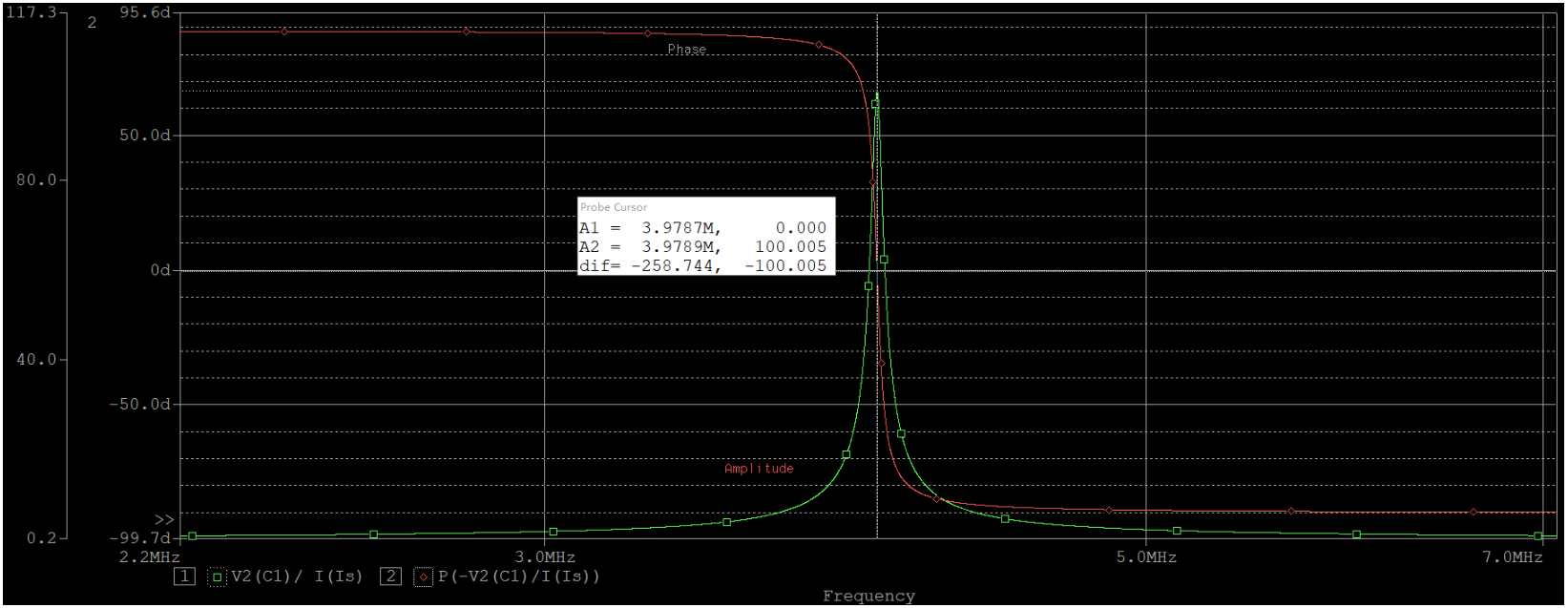
上圖是電路總阻抗的幅頻(綠線)和相頻(紅線)特性曲線。先來看相頻,當$f《3.9787MHz$時,相位角為正,說明電路呈感性;當$f》3.9787MHz$時,相位角為負,所以電路呈容性;而$f=3.9787MHz$時,電路呈電阻性,這說明此時電路諧振,實際測得的諧振頻率$f_0=3.9787MHz$。這個頻率值很接近我們計算所得的理論值。
我在仿真的時候,將每十倍頻的采樣點數故意設得非常高,也就是說結果的精確度等級幾乎可以達到0.0001。之所以強調這一點,是希望讀者注意到上面諧振頻率的誤差,即$0.0002MHz$,并非是由于軟件仿真導致的,而是我們的理論值出錯了。諧振角頻率$\omega_0 = \frac{1}{\sqrt{L C}}$成立的前提條件是$\omega_0 L 》》 r$,也就是公式中其實忽略了小r的影響,而真正零誤差的公式為$\omega_0 = \sqrt{ \frac{1}{L C} -\frac{r^2}{L^2} }$,用該公式計算出來的諧振頻率恰好就是圖中的$3.9787MHz$。當然,實際中基本都忽略r的影響,因為性能好的電路中,其影響真的是微不足道啊。
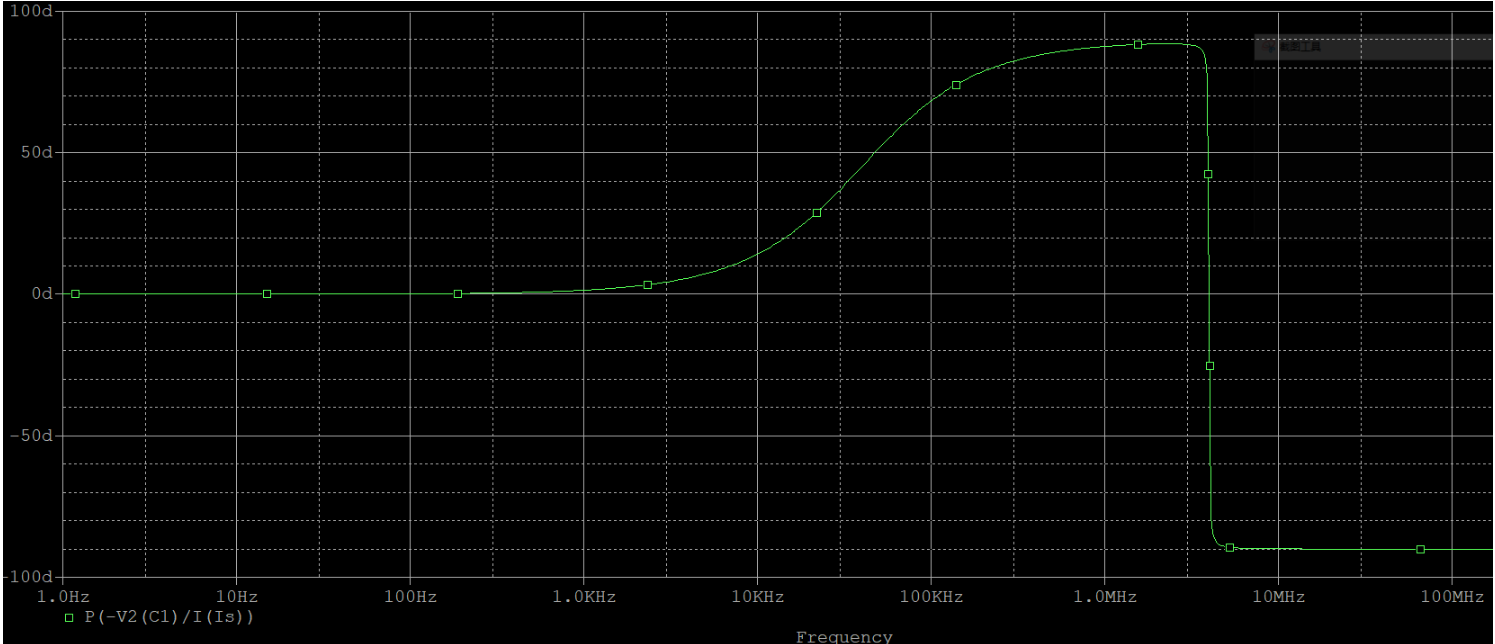
對于相頻曲線,還要關注的就是變化規律。如上圖所示,可以看到在諧振頻率附近,曲線的斜率非常大,變化得非常快。這說明,諧振點是個非常不穩定的點,很容易偏移到感性區域或者是容性區域,在實物電路的調節中相信這個問題會相當明顯并且棘手。此外,我們剛講過r對相頻的影響,這個再次體現在了低頻區域的相位上,大約在1MHz以下,相位就開始回零,最終趨于純電阻性。其原因可以通過阻抗或者導納公式推知,由于是低頻段分析,因此過程中可將${(\omega L)}^2$忽略簡化分析:
$Y(j\omega) = j\omega C + \frac{1}{j\omega L + r}=\frac{r}{r^2 + (\omega L)^2}+j[\omega C - \frac{\omega L}{r^2 + (\omega L)^2}] $
$When \; \omega L 《《 r ,Y(j\omega) = \frac{1}{r}+j[\omega C - \frac{\omega L}{r^2}]$
$\Theta (j\omega) = \arctan \omega (rC-\frac{L}{r})$
再看第一張圖中的幅頻,曲線呈尖峰狀。結合相頻曲線,可知在電路諧振時(是忽略r時的諧振,而非電路實際真正的諧振),阻抗的幅值達到最大,為$100 \Omega$。這里的$100 \Omega$恰好就是諧振電阻$R_0$。
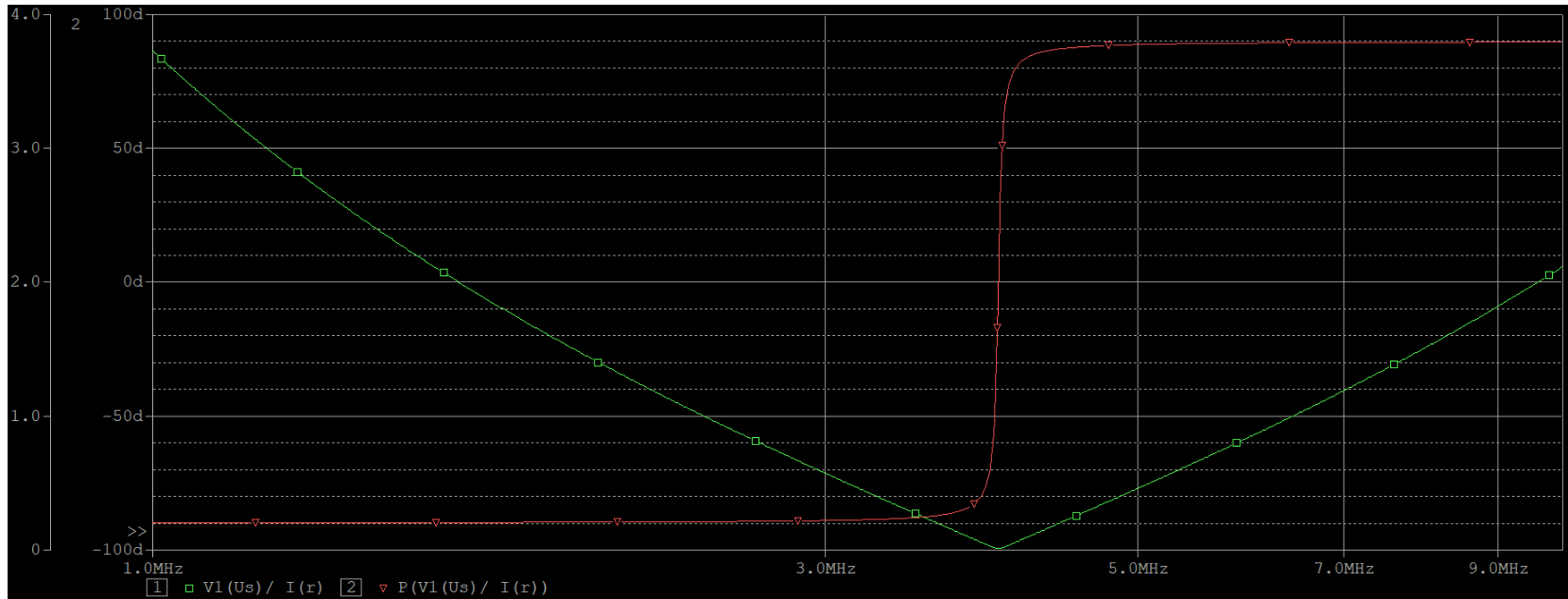
以上是并聯電路的阻抗特性,在串聯電路中,阻抗特性曲線如下圖所示,剛好和并聯相反。
選頻特性和通頻帶
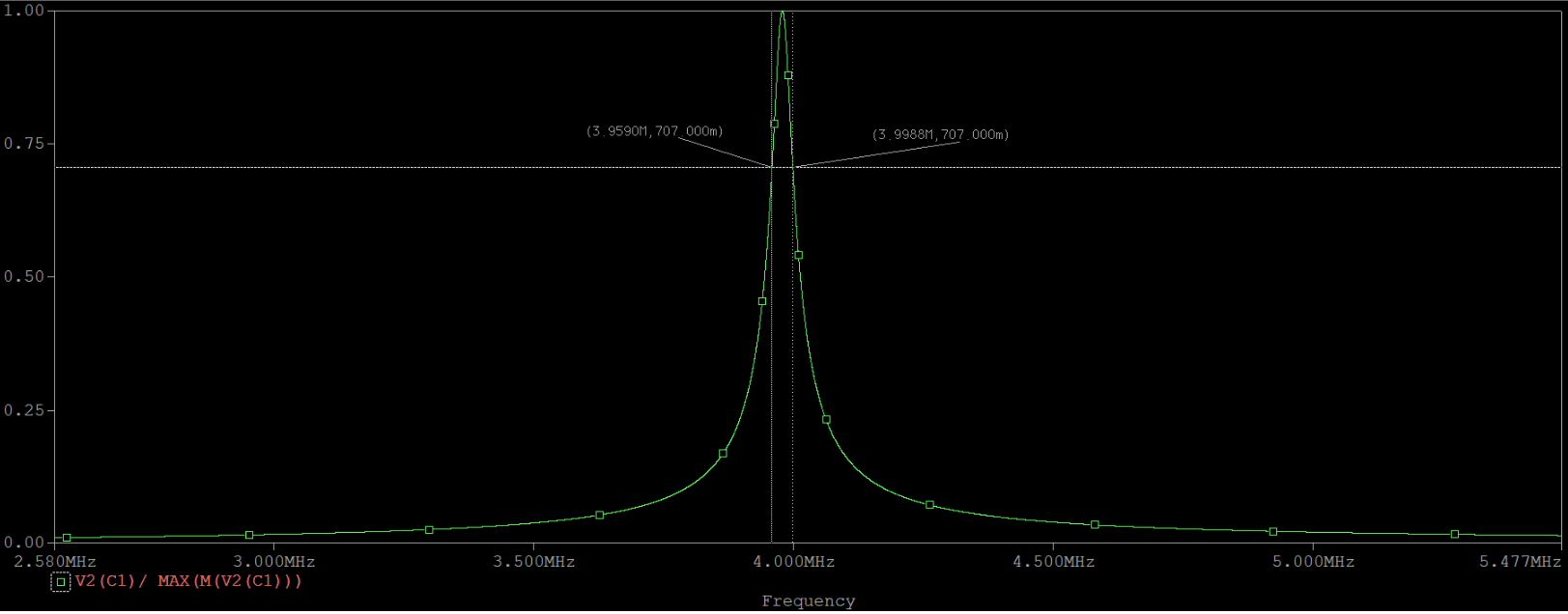
上圖是回路電壓的歸一化曲線,可以表示為$\frac{U(j\omega)}{U_0}$,通過一定變換,可知它與$\frac{Z(j\omega)}{R_0}$是等價的。直觀地說,上圖就是阻抗幅頻曲線歸一化后的樣子,并且$\frac{U(j\omega)}{U_0}$的相頻與阻抗相頻特性是完全一樣的。
這里,可以測得通頻帶大約為$39kHz$,允許通過的頻率范圍就是$3.959MHz$到$3.999Mhz$。結合理論公式,我們知道:通頻帶和選頻特性是矛盾的,因為選頻特性越好,要求品質因數要越大;如果通頻帶越大,則品質因數就要變小。所以,電路設計中要綜合權衡這兩個指標。
串聯電路的選頻特性曲線和并聯的一樣,也是呈尖峰狀,只不過用于衡量選頻能力的公式變為$\frac{I(j\omega)}{I_0}$。
諧振電路設計
并聯電路
一階LC諧振電路需要設計的參數無非就是電感L值和電容C值,而固有損耗通常都是客觀決定的。L、C值的選擇會影響電路的諧振頻率、諧振電阻、品質因數等特性。以并聯電路為例,下面討論參數的選擇問題。
首先,很明顯的一點是,$L·C$的值越小,諧振頻率越大;而且假設L、C各自減小到原來的一半,那么諧振頻率只增大兩倍,而不是四倍。
第二個是諧振電阻,將原來的公式進行變換可得$R_0=\frac{L}{C·r}$,由此可知L越大,C越小,那么諧振電阻就越大;而且如果L增大到原來的兩倍,C減小到原來的一半,那么諧振頻率仍然不變,但是諧振電阻卻增大了四倍。
品質因數跟諧振電阻有很大關系,將公式進行變換可得$Q_0=\sqrt{\frac{R_0}{r}}$,也就是說如果諧振電阻能夠增大到4倍,那么品質因數可以增大到2倍。
并聯回路的最大電壓就是諧振時候的電壓,該電壓值$U_0=I_{sm}·R_0$,它的增大趨勢和諧振電阻相同。
此外,我們必須要注意電感和電容的耐壓耐流特性。在并聯電路里,諧振時候流過電感和電容的電流幅值最大,并且滿足$|I_{C0}|=|I_{L0}|=Q_0|I_{sm}|$。其增大趨勢是和品質因數相同。
串聯電路
與并聯一樣,$L·C$的值越小,諧振頻率越大;而且假設L、C各自減小到原來的一半,那么諧振頻率增大兩倍。
諧振電阻取決于固有損耗值。
品質因數$Q_0=\sqrt{\frac{LC}{r^2}}$,L增大,C減小,可以增大品質因數。
串聯回路的最大電流就是諧振時候的電流,該電流值$I_0=\frac{U_{sm}}{R_0}$,與諧振電阻呈反比。
在串聯電路里,諧振時候電感和電容的分壓最大,并且滿足$|U_{C0}|=|U_{L0}|=Q_0|U_{sm}|$。其增大趨勢是和品質因數相同。
固有損耗對電路的影響
最后想要說明的一點就是固有損耗帶來的影響。因為仿真軟件里的模型一般都是理想的,也很難說固有損耗一般在哪個范圍。我嘗試了不同大小的固有損耗值,發現它對電路的影響還是比較有趣的。
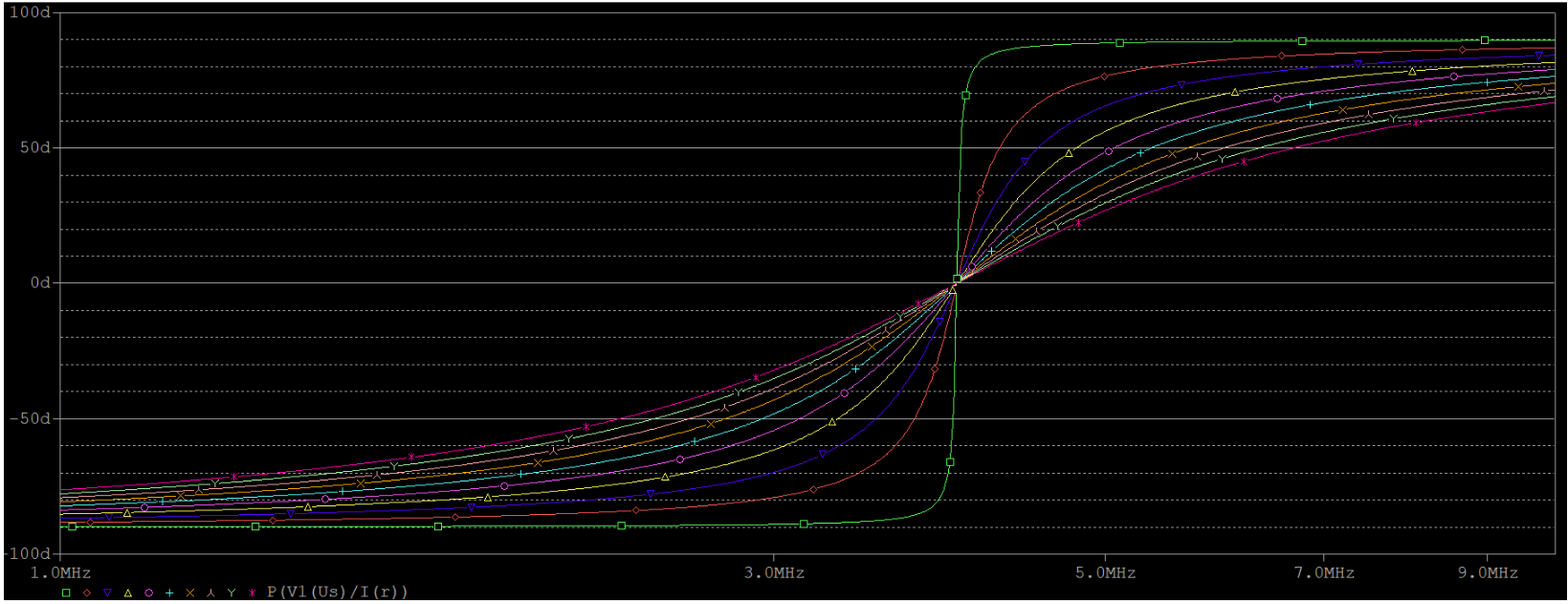
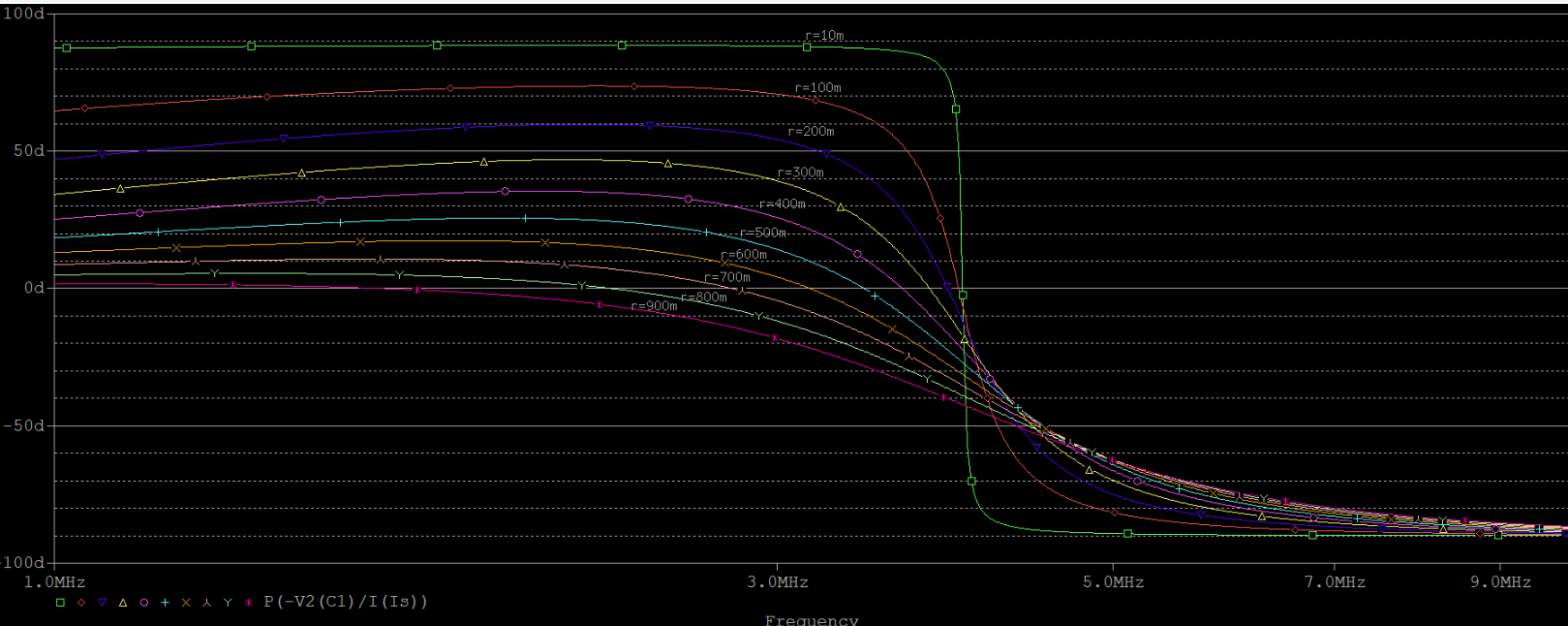
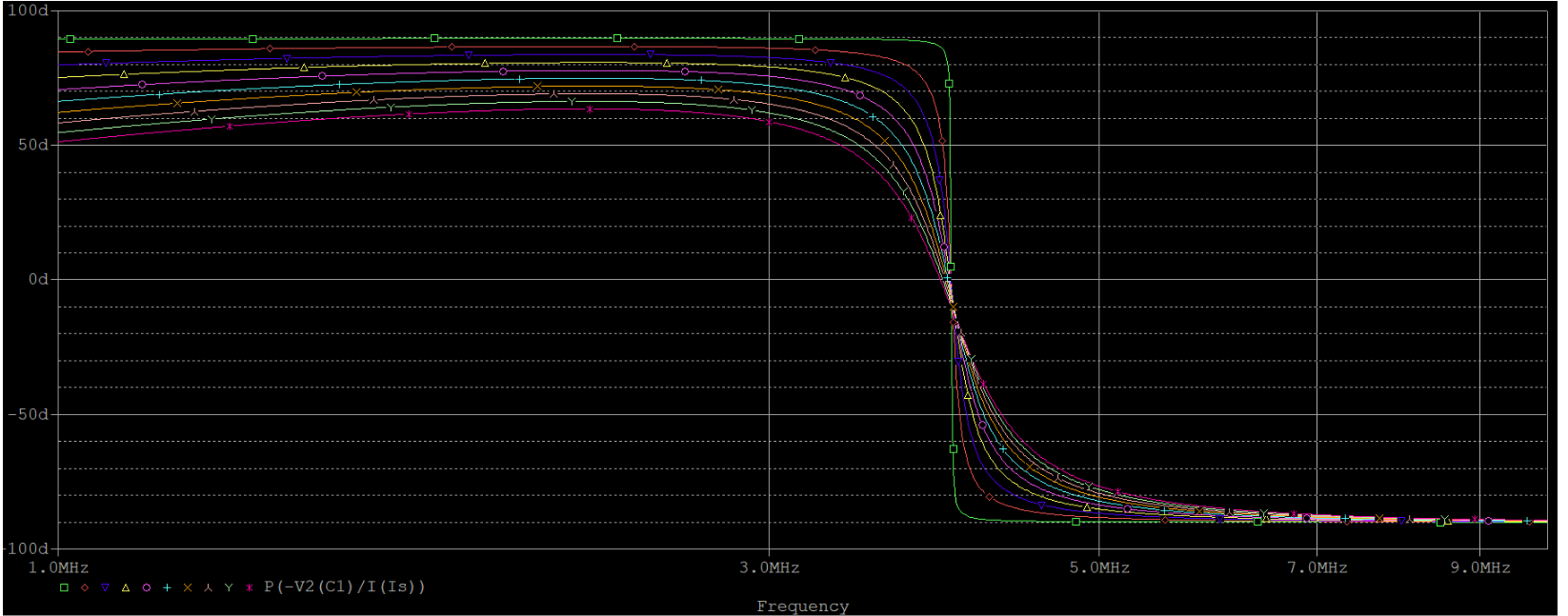
關于固有損耗對諧振頻率的影響,并聯和串聯電路表現得截然不同。串聯電路的諧振頻率絲毫不受干擾(上第一幅圖),并聯(上第二幅圖)的在上文就已經提到過了。我們看到,固有損耗從$10m \Omega$僅僅變到$900m \Omega$,諧振頻率就偏移了將近50%。解決這一問題的方法,就是一定范圍內增大L,從而保證$\omega_0 L 》》 r$這一前提條件。例如,就之前的仿真電路,將電感L調整為$200nH$,電感調整為$8nF$,此時諧振頻率仍然不變,但是對固有損耗的抵抗力顯然增強,如下圖所示(r的取值同上面):
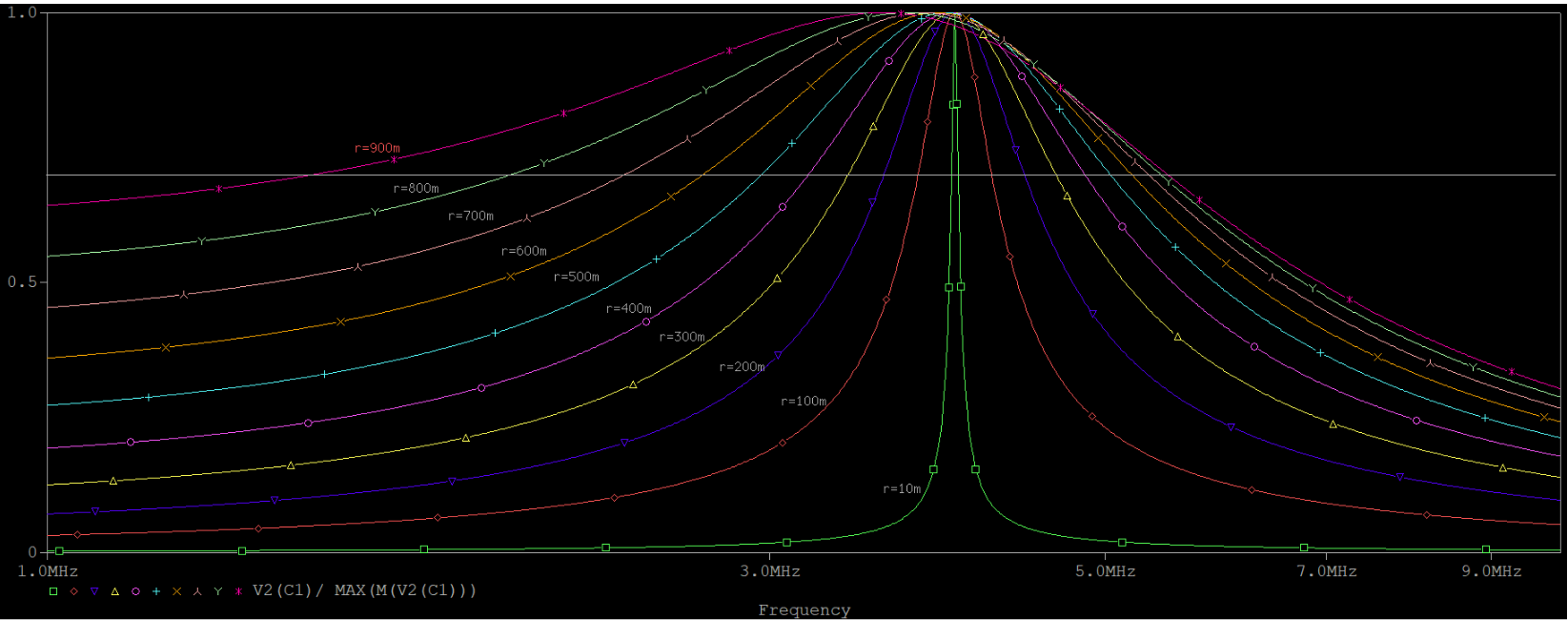
諧振電路最重要的特性除了諧振頻率,還有就是選頻特性或者說通頻帶。比較遺憾的是,同諧振頻率一樣,固有損耗對選頻特性的影響也非常大。如下圖所示,通頻帶的增大非常明顯,與之相反,我們可以觀察到波峰的位置偏移程度較小,也就是說電壓中心頻率對r是不太敏感的。該問題的解決方法與諧振頻率一樣。
除了諧振頻率和選頻特性,下面分析了其他特性的變化,這些變化的前提是$\omega_0 L 》》 r$。
諧振電阻方面,串聯電路中諧振電阻就是固有損耗電阻,因此r越大,$R_0$也越大;并聯電路中,$R_0=\frac{L}{C·r}$,所以$R_0$與r呈反比關系。
品質因數公式在串聯和并聯中互為倒數,但其實可以化成相同的形式:$Q_0=\sqrt{\frac{R_0}{r}}$。因此,品質因數也與r呈反比關系。
帶載LC諧振電路
以上的所有分析都是針對空載電路來說的,然而實際電路中,都是帶載的情況,此時為了獲得更好的選頻能力,該如何選擇L和C的值呢?
我們假設電感的固有損耗為$r$,負載電阻為$R_L$,則$Q_L=\frac{R_L//r}{\omega_0 L}=\frac{1}{rk+\frac{1}{R_Lk}}$,$k=\sqrt{\frac{C}{L}}$。如果要使品質因數最大,則要滿足$k^2=\frac{C}{L}=\frac{1}{R_Lr}$。進而,假設認為電感是理想的,沒有損耗,那么回路電阻完全取決于負載,此時$Q_L=\sqrt{\frac{C}{L}}R_{\Sigma}$,則C越大L越小,品質因數越大,選頻特性越好。
 電子發燒友App
電子發燒友App
























評論