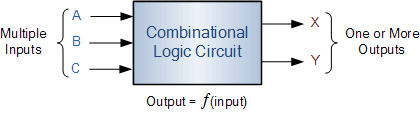
1. 靜態互補CMOS

實際上就是靜態CMOS反相器擴展為具有多個輸入。更反相器一樣具有良好的穩定性，性能和功耗。

靜態的概念：每一時刻每個門的輸出通過低阻抗路徑連到VDD或VSS上。任何時候輸出即為布爾函數值。

動態電路通常依賴把信號暫存在高阻抗節點的電容上。

1.1 閾值損失

互補結構PUN（pull up network)+PDN（pull down network)可以解決。

1.2 兩輸入與非門實例

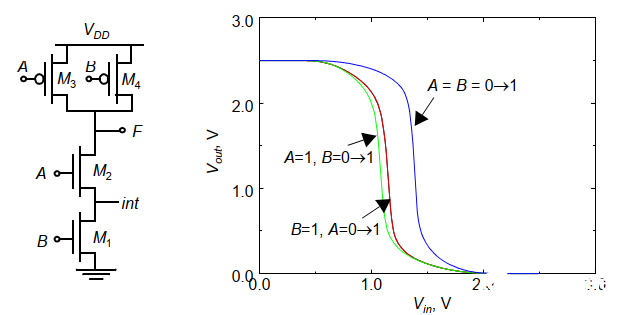
與非門的VTC曲線與輸入有關，從下圖可以發現，A=B=0時，PUN全部導通，對應強上拉，而當A或B中有不導通的時候，PUN中只有一個導通，相當于驅動能力下降（在反相器中提到P管驅動能力下降導致VTC左移，VM上漂），因此VTC左移到紅色和綠色線。
而紅綠兩線的主要區別在于NMOS的內部節點int上，由于體效應的緣故會使得M1和M2在分別導通時閾值電壓不同，VTC曲線會有微小的差異。

雖然互補CMOS是實現邏輯門比較簡單的方式，但是隨著扇入增加，會帶來兩個問題：

實現一個N扇入的門需要2N個器件，會增大實現面積。

互補CMOS的傳播延時隨著扇入增大迅速增大（無負載本征延時在最壞時與扇入成二次函數關系）

1.3 延時與扇入的關系

例如對于一個四輸入與非門：

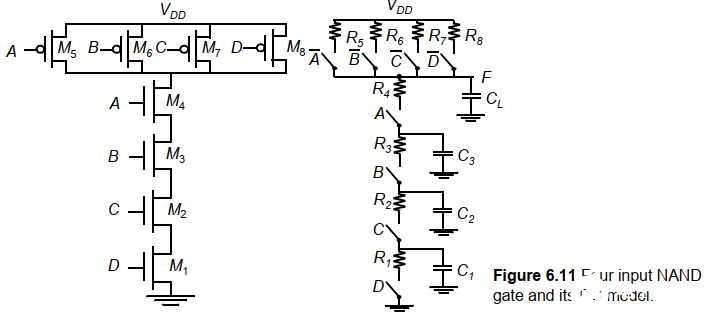
在最壞情況下，PUN只導通一條通路，此時從低到高的延時tpLHtpLH最大，當增大扇入數，PUN的器件隨著扇入線性增加，電容也線性增加，但最壞情況PUN的等效電阻不變，因此tpLHtpLH隨著N的增加呈線性增加。

而對于PDN,串聯會使得門進一步變慢。在PDN中分布RC網絡帶來的延時與串聯鏈元件數呈平方關系。因此tpHLtpHL是輸入的二次函數：tpHL=a1FI+a2FI2+a3FOtpHL=a1FI+a2FI2+a3FO,其中FI=扇入，FO = 扇出。

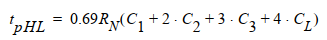
下圖是NAND門的本征傳播延時與扇入的關系曲線：

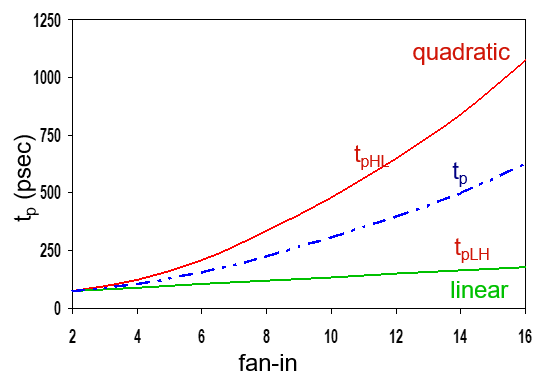
1.4 解決大扇入的方法

增大晶體管尺寸。可以減少串聯電阻。

局限：會增加寄生電容。只有當負載以扇出電容為主時有用，否則只會增加"自載效應"。

逐級加大尺寸。因為從公式中可以看到M1-M4的電阻出現次數依次遞增，所以因該讓他們的電阻值依次遞減才能得到最優解。

局限： 在實際版圖中不易實現。

重新安排輸入。由于輸入信號不都在同時間到達，因此可以把關鍵信號放到靠近輸出端的晶體管上以提高速度。（關鍵信號：在所有輸入中最后到達穩定值的信號）

重組邏輯結構。比如，將6輸入OR門變為兩個三輸入NOR門加上一個二輸入與非門。原理是減小了扇入。

問題：為什么把關鍵信號放到靠近輸出端的晶體管上可以提高速度？
其實就是一個放電順序的問題：

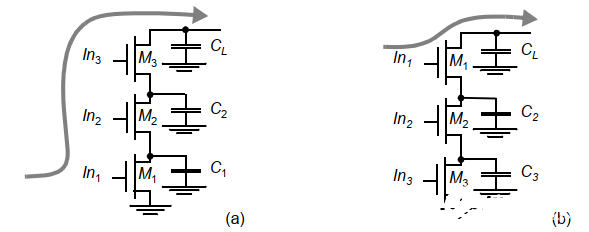
上圖中，如果M1是最后才導通的那個，則直到M1導通前CL和C2都無法放電。而把M1放到最上面以后，C2和C1就可以先放電，節省了時間。

2. 組合邏輯性能優化

跟反相器鏈的性能優化類似，前面已經知道對于一個CL負載，驅動其的最優每級扇出f=(CL/Cin)1/Nf=(CL/Cin)1/N,并且最優扇出保持在4左右。
那么對于任何組合邏輯而言，又該如何呢？
這里將原來的反相器鏈（上面的公式）改寫為（下面的公式）：

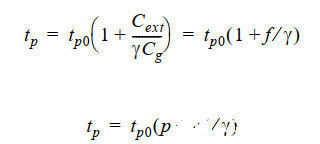
其中，ff仍然是等效扇出，此外，在這里也稱為電氣努力（electrical effort）。pp代表復合門與簡單反相器的本征延時比，與門的拓撲結構和版圖樣式有關。下面是一些pp的典型值：

2.1 邏輯努力，門努力

系數gg稱為邏輯努力（logical effort)。可以有下面幾種表達方式：

他表示對于給定負載，復合門必須比反相器更努力工作（電流）才能得到類似響應。

當邏輯門的每個輸入的輸入電容跟一個反相器相同，在產生輸出電流方面比這個反相器差多少。

當邏輯門的輸出電流與一個標準反相器相同時，它的輸入電容是反相器的多少倍。
下面是一些常用門的邏輯努力：

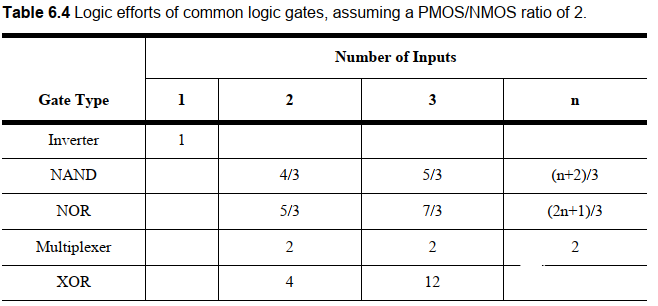
下面這個例子可以直觀地理解邏輯努力的含義：

對于一個最小尺寸反相器，其P管尺寸是N管2倍。因此輸出電容是N管電容（CunitCunit）的3倍。為了確定NAND和NOR的尺寸，如果要保證輸出電流相同，也就是等效電阻和標準反相器相同。這就提出了要求：PUN等效尺寸=2，PDN等效尺寸=1.對于并聯來說，等效電阻=最壞情況也就是只有一個導通的電阻，所以PMOS尺寸仍為2；對于串聯，尺寸變大一倍，等效電阻變為一半。
由此可見，NAND尺寸變換后等效的輸入電容變為4Cunit4Cunit。也就是最小反相器的4/3.也就是邏輯努力為4/3。同理，NOR的邏輯努力為5/3。

一個邏輯門的延時可以分為兩部分，努力延時和本征延時：

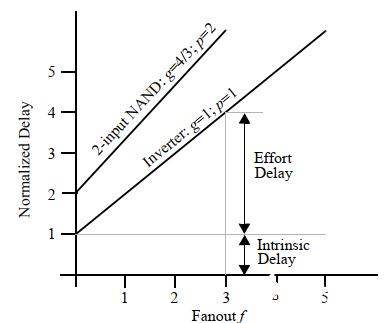
上圖中，直線斜率就是邏輯努力，y軸交點就是本征延時。此外，把?h=gfh=gf稱為門努力（gate effort)。

2.2 組合邏輯鏈最小延遲計算

組合邏輯鏈的延時可以表示為：

從反相器鏈的結論來看，要使得上式有自小值，需要使得每一級的門努力相同。我們做如下定義： 1. **路徑邏輯努力(path logical effort):**?G=∏N1giG=∏1Ngi

分支努力（branching effort):?b=Conpath+CoffpathConpathb=Conpath+CoffpathConpath.分支努力其實就是表示在該路徑上本級的輸出負載與流入下一級的有效負載的比值。

路徑分支努力（path branching effort):?B=∏N1biB=∏1Nbi

路徑電氣努力:?F=∏N1fibi=∏fiBF=∏1Nfibi=∏fiB

總路徑努力:?H=∏N1hi=∏N1gifi=GFBH=∏1Nhi=∏1Ngifi=GFB

因此，與反相器鏈類似，使得延時最小的門努力為：

h=H??√Nh=HN

所以最小延時為：

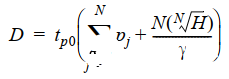
3. CMOS邏輯門中的功耗

復合CMOS邏輯門的功耗和反相器中討論的類似，也是與以下幾個因素有關：

器件尺寸（電容）

輸入和輸出上升下降時間（決定短路功耗）

器件閾值和溫度（影響漏電功耗）

開關活動性（開關功耗）

當門比較復雜的時候，受影響最大的是開關活動性α0?>1α0?>1，可以分為兩部分：

只與邏輯電路拓撲結構有關的靜態部分

由時序特性引起的動態部分（虛假尖峰信號或毛刺Glitch)

3.1 開關活動性的靜態部分

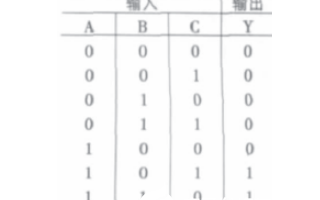
靜態部分與所實現的邏輯功能（真值表）密切相關。例如：對于一個N輸入的NOR門，假設papa和pbpb表示輸入A和B分別為1的概率，且輸入不相關（這個假設很難成立）。則輸出為1的概率為：p1=(1?pa)(1?pb)p1=(1?pa)(1?pb),這個表達式是根據真值表推導出的。
則由0到1的翻轉概率為：

α0?>1=p0p1=(1?(1?pa)(1?pb))(1?pa)(1?pb)α0?>1=p0p1=(1?(1?pa)(1?pb))(1?pa)(1?pb)

下圖展示了這種關系：

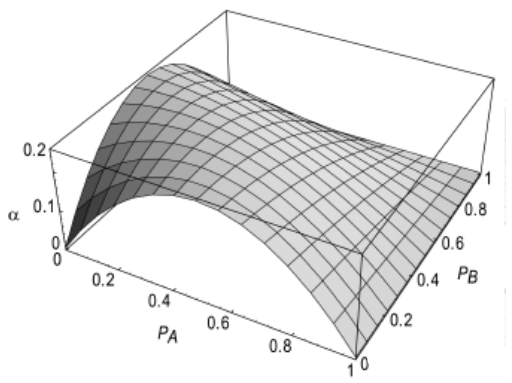
上面算法的局限性：

不適用于在時序電路中出現的具有反饋的電路。

其假設每個門的輸入信號概率不相關是很少見的。

3.2 開關活動性的動態虛假翻轉

從一個邏輯塊到另一個邏輯塊的非零傳播延時可能會引起毛刺或動態故障(dynamic hazard) 的虛假翻轉。在一個時鐘周期內節點在穩定到正確電平之前可以多次翻轉。下面這個例子可以解釋這種虛假翻轉：

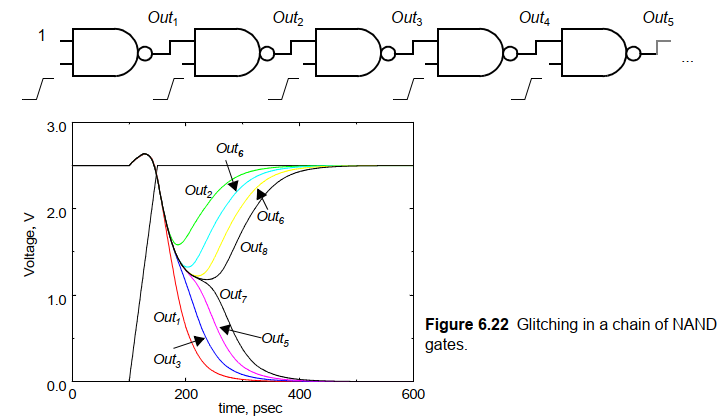
上圖是一個NAND門鏈在輸入同時從0->1時的響應。開始時輸入為0，所以說有節點的輸出均為1。當出現輸入的翻轉時，理論上最終的輸出奇數位都是0，偶數為都是1。但是從圖中可見out1在一定延時后降為0（紅線），由于存在這個延時，導致out2的輸出在out1穩定之前（相當于NAND輸入11）,會有像0翻轉的趨勢，直到out1基本穩定下來（趨于0）時，out2才又往1翻轉。導致了圖中的綠色線。

虛假翻轉的危害：

偶數位上的這些毛刺造成了邏輯功能外的額外功耗（因為從邏輯分析來看這些位不應該變化）。雖然這個例子中毛刺并不是軌到軌的變化，但是卻可能構成很大的功耗。

對于一些加法器，乘法器，會出現比較長的邏輯門鏈，毛刺功耗就很容易成為主要部分。

3.3 降低組合邏輯的開關活動性

邏輯重組：

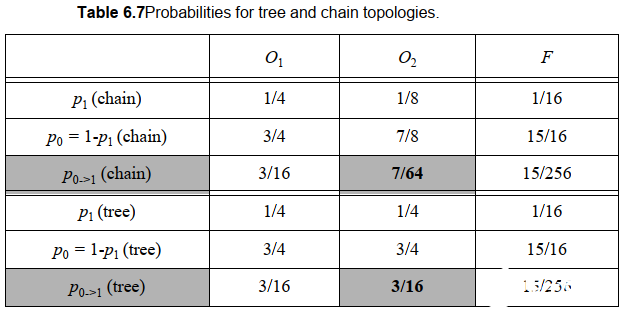
下面是4輸入與門的兩種實現，鏈式結構和樹形結構。如果不考慮上面提到的虛假翻轉毛刺，從開關活動性來看鏈式的結構具有更低的靜態活動性。

但是實際上也要考慮時序特性，考慮毛刺功耗，因為樹形結構沒有任何毛刺活動（每級信號延時都相等）。

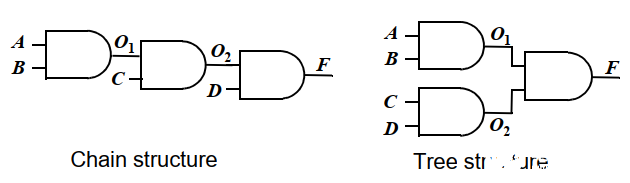
輸入排序：

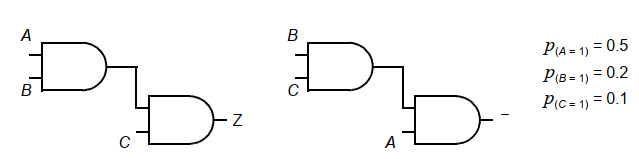
將具有較高翻轉率的信號放到靠近輸出端的輸入端上。

可以看下面的例子,首先兩個電路輸出的翻轉率是相同的，主要看中間節點。對于第一種，活動性等于(1?0.5?0.2)(0.5?0.2)=0.09(1?0.5?0.2)(0.5?0.2)=0.09.而對于第二種，活動性等于(1–0.2?0.1)(0.2?0.1)=0.0196(1–0.2?0.1)(0.2?0.1)=0.0196

分時復用資源：

分時復用某個硬件資源（邏輯單元或總線）來完成多個功能。

通常可以減小面積，但不是總能降低開關活動性。例如下面的例子：

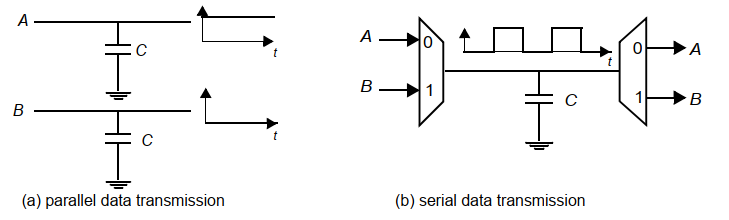
電容減少為一個，但是可能需要倍頻來實現數據的傳送，所以對應的開關等效電容是一樣的。

但是對于傳遞的數據有一些特性時，分時復用可能收效不高，比如A總是1,B總是0。并行傳輸時的切換非常少，而分時復用則會有較大翻轉。

通過均衡信號路徑減少毛刺：?毛刺主要是電路中路徑長度失陪引起的。因此要解決路徑中延時長度不同的問題，可以使用樹型結構替換鏈式結構。

4. 有比邏輯

4.1 偽NMOS

有比的概念：輸出電平和功能取決于NMOS和PMOS的尺寸比。不同于無比邏輯，無比邏輯高低電平與尺寸無關。

目的：有比邏輯的目的是減少晶體管數。從2N降低為N+1.

思路：將PUN替換為一個無條件負載器件。通常為一個柵極接地的PMOS負載（偽NMOS門）。

缺陷：

會降低穩定性和額外功耗。

額定低電壓不是0，因為存在PDN和偽NMOS的通路。這降低了噪聲容限，并且引起了靜態功耗。

例子：偽NMOS反相器。
縮小PMOS器件的尺寸可以得到不同的電壓傳輸曲線：

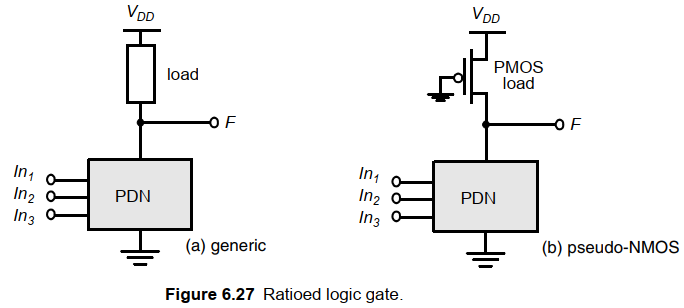
其額定低電壓，靜態功耗以及延時隨著尺寸的變化如下表：

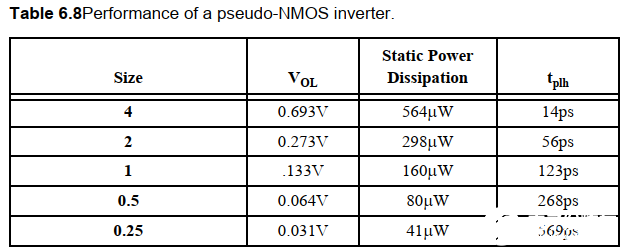
雖然靜態功耗限制了偽NMOS的應用，但是當面積是最重要的因素時，偽NMOS還是可以使用的，因此還是可以看到偽NMOS有時應用在大扇入的電路中。

4.2 差分串聯電壓開關邏輯(DCVSL)

目的：完全消除靜態電流并提供軌到軌的電壓擺幅的有比邏輯。

原理：差分邏輯和正反饋。

差分門要求每個輸入都具有互補形式，同時也產生互補輸出。

反饋機制保證不需要負載時將其關斷。

例子：XOR-XNOR門

上圖中，下拉網絡PDN1和2是互斥的，同一時間兩只只會有一個導通。
假設最初out為高，out非為低。當PDN1導通時，out下拉。但是PDN1必須足夠強勁使得out低于VDD-|VTP|，才能使得M2導通，out非變為VDD,最終將M1關斷。

優勢：

消除靜態電流，提供軌到軌輸出

同時產生了輸出和其反信號，節省了額外的反相器，避免使用反相器引起的時差問題。這實際上受益于差分邏輯。

缺陷：

在翻轉期間PMOS和PDN會同時導通一段時間，產生短路通路，造成渡越電流。（不同于靜態電流，靜態電流在PDN導通時一直存在）

在實際布線時導線數量加倍，使得電路復雜

動態功耗較高

4.3 傳輸管邏輯

目的：減少晶體管數

原理：輸入驅動柵極和源漏端來減少邏輯需要的晶體管數。只允許驅動柵極的CMOS不同。

缺陷：存在閾值損失。并且由于體效應這種情況更加嚴重。如下圖：

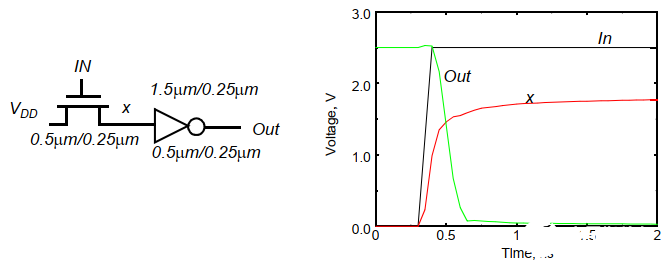
此外，應該避免傳輸管驅動另一個柵極，這樣會導致閾值損失傳遞：

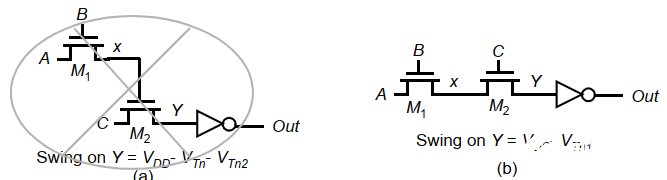
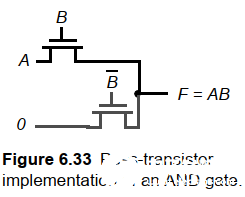
傳輸管的VTC與CMOS反相器不同，下圖是一個而輸入AND傳輸管的VTC:

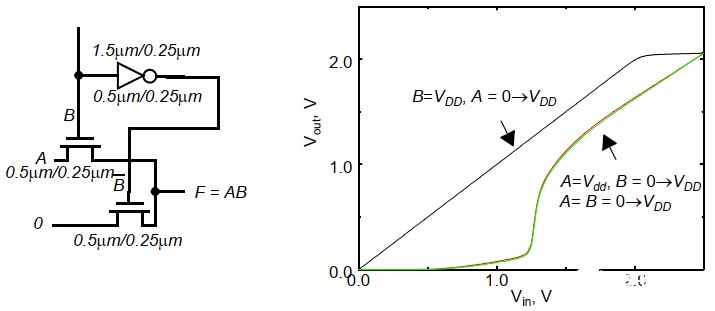
可見一個傳輸門是不能使信號再生的。經過多級后會衰減，可以通過插入反相器來彌補。

4.3.1 差分傳輸管邏輯CPL

高性能設計中通常使用差分傳輸管邏輯，稱為CPL或DPL.

CPL屬于靜態門，輸出節點通過低阻路徑連到VDD或地。

具有模塊化特點，門單元庫設計簡單。

4.3.2 解決閾值損失和靜態功耗

問題：由于傳輸管在高電平無法充電到VDD,少了一個VT,所以在驅動后級的反相器時反相器會有靜態功耗。

a. 電平恢復器

一種簡單的方法是使用一個PMOS連到反饋環路中：

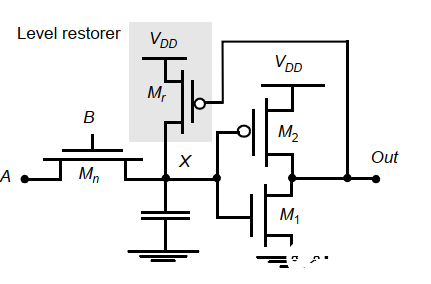
優勢：通過上拉的PMOS將高電平充到VDD,消除了后級反相器的靜態功耗，傳輸管和恢復器中也沒有靜態電流路徑。

缺陷：

是有比邏輯，增加了復雜性。在節點從高到低的過程中，傳輸管試圖拉低節點，而電平恢復器卻要上拉到高，因此傳輸管的下拉能力必須大于恢復器的上拉能力。這就要求仔細設計各個管的尺寸。

電平恢復器對器件切換速度有影響。增加恢復器增加了內部節點X的電容，減慢了門的速度。

b. 多閾值晶體管

使用0閾值的NMOS傳輸管可以消除大部分閾值損失。所有非傳輸管都用高閾值器件實現。

缺陷：

需要對器件的注入準確控制才能達到0閾值，并且由于體效應，難以真的達到全擺幅

用零閾值對功耗有不利影響。這是因為即使器件關斷，也會有亞閾值電流流過傳輸管，如下圖：

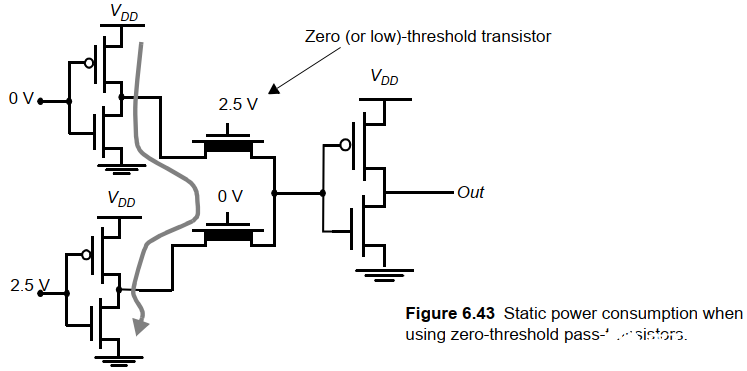
c.傳輸門邏輯

最廣泛采用的是傳輸門邏輯，利用N和PMOS的互補特性。

兩個管子并聯，控制信號相反，任何時候兩者都導通。通常消耗更少的管子。例如實現下面的邏輯：

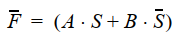
采用CMOS邏輯需要8管，而傳輸門邏輯只需要6管。（不包括反向輸入信號的生成）

4.4 傳輸門的性能

傳輸門的高到低和低到高等效電阻基本上可以認為是定值，下圖是傳輸門從低到高的翻轉的等效電阻：

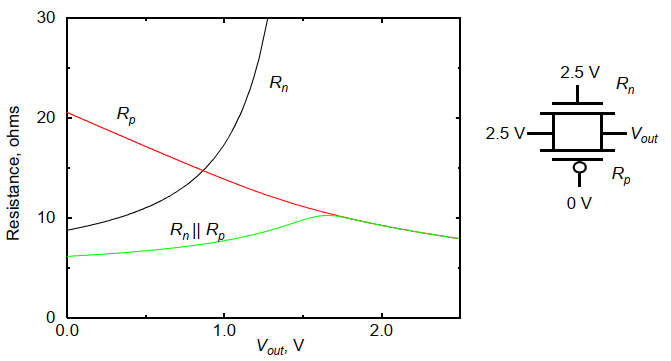
傳輸門鏈：
對于傳輸門鏈可以使用一階近似將其等效為電容電阻網絡：

其延時可以通過Elmore近似計算得到：

可見傳輸門延時正比于n2n2，因此不能采用過長的傳輸門鏈。如果要使用，建議是在傳輸門鏈中每隔幾個（3~4）傳輸門插入一個Buffer。

5. 動態CMOS邏輯

在PUN和PDN上下插入CLK控制的管子。主要有兩個階段：預充電和求值。由CLK決定。

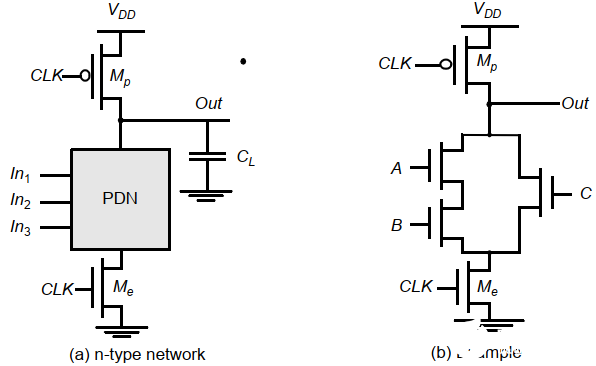
預充電：
CLK=0時輸出節點Out被PMOS管預充電至VDD。此期間NMOS求值管關斷，所以下拉不工作。求值管消除了預充電期間的任何靜態功耗。
求值：
CLK=1時，預充電管關斷，輸出根據下拉拓撲結構有條件地放電。

優點：

邏輯功能只有下拉網絡實現，晶體管數少，為N+2個

是無比邏輯，功能與尺寸無關。

只有動態功耗。理想情況下不存在VDD到GND的靜態電流路徑。但總功耗還是可能明顯高于靜態邏輯

有較快的開關速度。因為減少了晶體管數，每個扇入只連接到一個負載晶體管，降低了負載電容。相當于降低邏輯努力。另外，動態門沒有短路電流。

當然也可以用P型動態門，也就是預充電通過下拉的NMOS實現，但這種的缺點是比n型動態門慢。因為PMOS的驅動電流小。

動態邏輯的噪聲容限是極不對稱的，比如一個四輸入NAND門：

下表是其各項性能參數：

假設輸入連在一起，則這個門的開關閾值VM=VTN,高電平噪聲容限將有VDD-VTN這么多。
此外，其低到高的傳播延時為0，因為預充電后輸出總是高電平，對于低電平的輸入沒有任何變化發生。

實際上，該門的開關閾值與時鐘周期有關，下圖是不同glitch下該門的響應。可以發現，對于較大的輸入翻轉，門變化較快。而輸出電壓下降的幅度實際上還與周期有關，如果求值時間很短，那么噪聲電壓比如很大才能破壞信號。

缺陷：

動態邏輯的時鐘功耗可以很大

當增加抗漏電器件時可能會有短路功耗

由于周期性的預充和放電，動態邏輯會有較高的開關活動性。

5.1 動態設計的信號完整性

a. 電荷泄露

預充電到高后，電容上將保持高電平，但總是會有泄露電流導致電荷漏掉。如下圖：

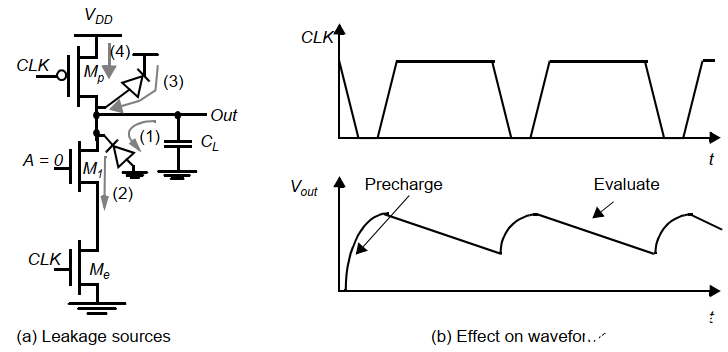
可見存儲在CL上的電荷將通過漏電左圖的幾個漏電渠道漏掉，因此動態電路有一個最低的頻率要求，一般為幾KHZ。
解決方法：
電荷泄露的解決通常通過增加偽NMOS上拉以及反饋來補償：

通過反饋來控制上拉管可以降低靜態功耗。通常泄露器的尺寸比較小，以保證下拉網絡可以下拉。

b. 電荷分享

下圖展示了電荷分享。在求值期間，假設B=0，A置高后Ma導通，CL上的電容會在CL和Ca之間重新分配，導致輸出電平的降低。

解決方法：
通過對關鍵的內部節點預充電：

代價是面積和功耗。

c. 電容耦合

輸出節點較高的阻抗使得電路對串擾很敏感。

當有導線在動態節點上或鄰近時，會產生耦合電容破壞浮空節點。

回柵耦合（backgate)，輸出耦合至輸入。

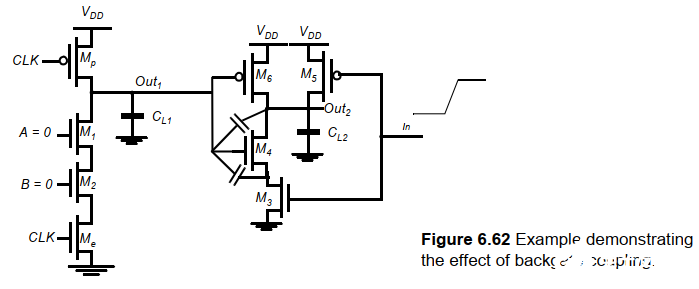
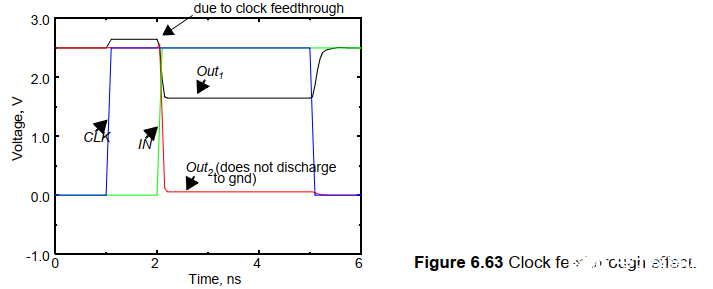
d. 時鐘饋通

電容耦合的特殊情況。在預充器件的時鐘輸入和動態節點之間的電容耦合引起。耦合電容由預充器件的柵漏電容組成。
其次，快速上升和下降的時鐘邊沿會耦合到信號節點上。例如上圖中顯示的那樣。

5.2 動態門的串聯

動態門的串聯會遇到延時的問題，例如下面的電路：

當Out1開始放電時，此時Out2應該維持不變，但是out1放電需要時間，導致out2也開始放電，產生錯誤。 但是如果每一級動態門在預充電后輸出都為0，則不會由這樣的問題。這也是動態門串聯的條件。

多米諾邏輯：

動態邏輯后加一個反相器，再級聯其他多米諾邏輯。反相器可以保證動態邏輯再預充電后輸出為0，避免1->0的翻轉。

np-CMOS:

使用n型動態邏輯和p型動態邏輯串聯，避免引入額外靜態反相器。

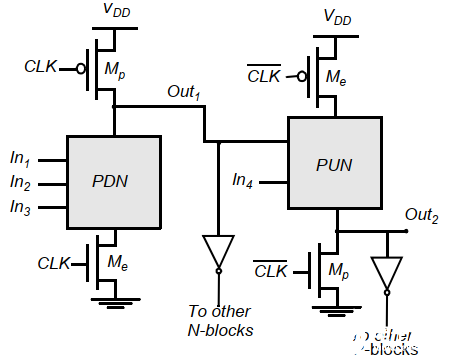
n型預充電為高，因此不會導致下一級的PUN提前導通。