為確保系統滿足所需的精度規范,透徹了解不同的誤差源非常重要。決定信號鏈精度的最關鍵要素之一是A/D 轉換器 (ADC),這是本文的重點。請記住,ADC 的精度可以用絕對精度、相對精度和總未調整誤差 (TUE)來表征。
一個偶爾讓年輕工程師感到困惑的常見問題是:精度與分辨率有何關系?例如,我的 12 位 ADC 是否也是 12 位精度的?
ADC 設計參數——分辨率
分辨率指定了 ADC 特性曲線中的步數(step)。對于具有統一步長的理想 ADC,分辨率決定了模擬輸入電壓的最小變化,使輸出變化一個計數。例如,具有 12 位分辨率的 ADC 可以解析 2^12中的 1 部分(part)(4096 中的 1 部分)。換句話說,12 位 ADC 可以檢測小至滿量程值的 0.0244% 的電壓。然而,這并不意味著轉換誤差(ADC 輸出的輸入和模擬等效值之間的差異)小于 0.0244%。
分辨率主要是一個設計參數,而不是性能規格。它沒有指定實際由非理想效應(如 ADC 非線性、偏移和增益誤差)決定的轉換誤差。
ADC 精度:當精度低于分辨率時
在數據轉換器中,通常用位數來表示精度。例如,我們可以說這個 ADC 是 12 位精度的。這意味著轉換誤差小于滿量程值除以 2^12。換句話說,轉換誤差小于一個 LSB(最低有效位)。
考慮到這一點,這可能不是表達性能準確性的準確方法,因為不清楚該特征中實際包含哪些誤差源。然而,它似乎通常指的是偏移、增益和積分非線性 (INL) 誤差的綜合影響。轉換器的精度可能遠低于其分辨率。
例如,考慮下面圖 1 中所示的 12 位 ADC。
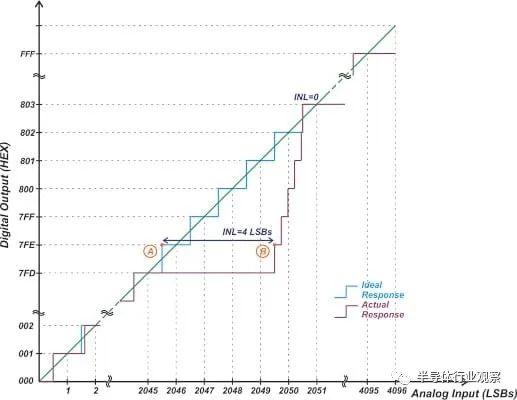
圖 1. ?12 位 ADC 示例。
圖中,藍色和紫色曲線分別是理想特性曲線和實際特性曲線。在這個特定的例子中,偏移和增益誤差被校準掉了。代碼 7FD 的寬度為 5 個 LSB,這導致代碼 7FE 處出現 4 個 LSB 的 INL 錯誤。此代碼中的錯誤由以下原因給出:

由于轉換誤差等于滿量程值除以 2^10,我們稱其精度為 10 位。上圖應該可以幫助您更好地理解這一點。首先,請注意,對于給定的滿量程值,10 位系統的步進比 12 位系統的步進寬 4 倍。在 12 位系統中,A 點和 B 點之間的差異為 4 LSB,而在 10 位系統中僅為 1 LSB。因此,公式 1 和 2 告訴我們,INL 為 4 LSB 的 12 位系統引入的誤差等于 INL 只有 1 LSB 的 10 位系統產生的誤差。
從 INL 誤差的角度來看,這兩個系統具有相同的性能。但是,這并不意味著這兩個系統完全相同。例如,12位系統的最大量化誤差?比10位系統小四倍(或者說12位系統的量化噪聲功率小16倍)。
為了更容易地計算精度,我們可以使用以下等式:
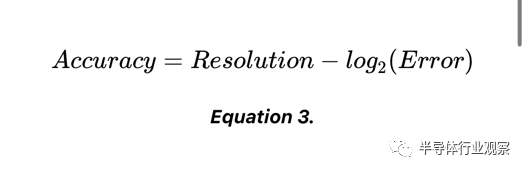
這可以簡化為:
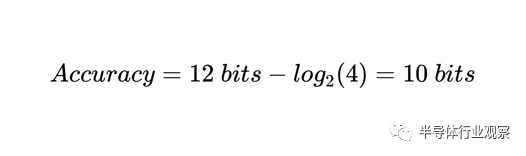
由于轉換誤差等于滿量程值除以 2^6,我們可以說其精度為 6 位。具有 6 位精度的三位 ADC 意味著什么?這意味著我們的 3 位 ADC 產生的誤差與 INL 為 1 LSB 的 6 位 ADC 產生的誤差相同。也就是說,我們ADC的步進是精確控制的(優于ADC的位數)。因此,ADC 僅引入了超出其量化誤差的少量誤差。
同樣,我們可以使用公式 3 計算 ADC 精度并得到:
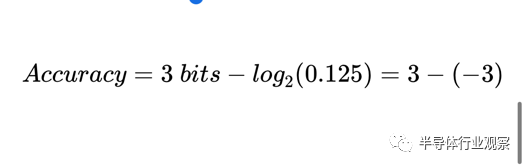
分段和兩步 ADC 簡介
讓我們從稍微不同的角度來研究上述 3 位 ADC,以更好地理解為什么可能需要比分辨率更高的精度。
假設我們有一個理想的三位數模轉換器 (DAC)。我們可以使用此 DAC 將 ADC 輸出轉換回模擬信號。從原始模擬輸入中減去 DAC 輸出,我們可以找到 3 位量化器的量化誤差(或“殘留”信號)。這在圖 3 中進行了說明。
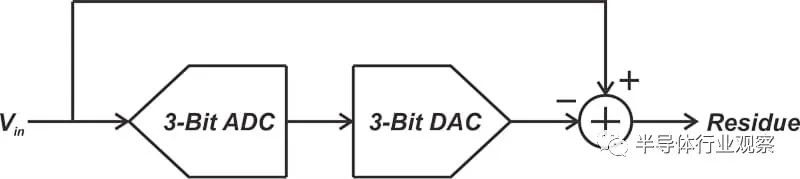
圖 3. 顯示從 ADC 輸入減去 DAC 輸出的“殘留”信號的示例圖。
雖然 ADC 的分辨率只有 3 位,并引入了較大的量化誤差,但其線性誤差相對較低。由于量化誤差是主要的誤差來源,因此可以通過第二個 ADC 進一步處理殘留信號,以產生高于 3 位的整體分辨率。這是可能的,因為 3 位 ADC 的線性誤差不會破壞我們的信號。我們只需要將 3 位 ADC 的大量化誤差再數字化一次,即可獲得更精細分辨率的整體 ADC。這實際上是分段和兩步 ADC 的工作原理。圖 4 顯示了這些 ADC 的更詳細框圖。????
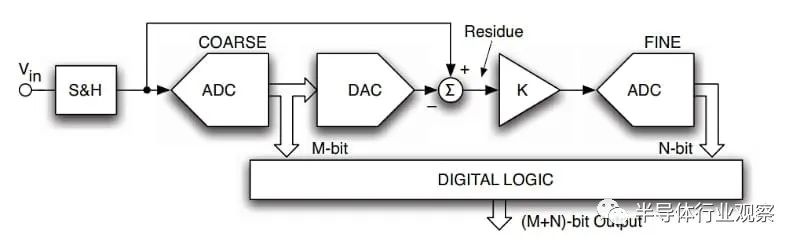
圖 4. 分段和兩步 ADC 的示例框圖。
第一個 ADC 執行粗略轉換并確定最終輸出中最高有效位 (MSB) 的 M 位。然后殘留信號由第二個 N 位 ADC 處理。第二級執行精細轉換并生成輸出的 N 位 LSB。這種結構允許我們用轉換速度換取功耗和硅片面積。例如,兩步架構需要的比較器數量明顯少于全閃存轉換器。
對于兩步架構,粗略 ADC 的精度需要比其分辨率好得多。除了粗ADC,DAC和減法器對殘差信號的精度也起著關鍵作用。這就是為什么要仔細確定每個模塊的最大允許誤差,以實現一定的整體精度性能。
現在我們已經確定了分辨率和精度之間的差異,讓我們看一個簡單的例子,看看我們如何計算具有非零偏移和增益誤差的 ADC 的精度。
使用 TUE 評估精度——非零偏移和增益誤差
根據設計目標,可以使用絕對精度或相對精度定義來計算公式 3 中的“誤差”項。實踐中常用的更好選擇是 TUE 規范。可以使用增益、偏移和 INL 誤差的最大值的和方根 (RSS) 來計算最大 TUE。這可以在下面的等式中看到:
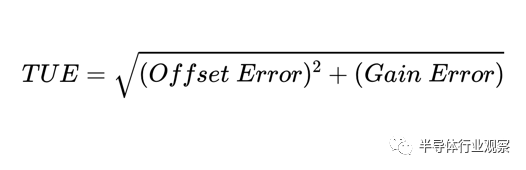
RSS方法基于誤差項不相關的假設,因此所有誤差項同時處于最大值的概率很小。例如,使用這種方法,我們可以假設對于 12 位 ADC,我們有:
INL?= 3 LSBs
Offset error = 2.5 LSBs
Gain error = 3 LSBs
假設應用于 ADC 的模擬輸入可以在 ADC 的整個輸入范圍內取值,我們可以將總誤差估算為:

現在,應用等式 3,我們得到:
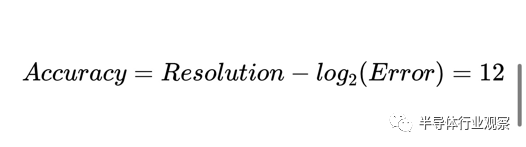
我們有時將公式 3 得到的精度稱為“精度的有效位數”。如果我們應用校準來抵消偏移和增益誤差,我們將只剩下 INL 誤差。請注意,為了使用 TUE 方程,所有誤差項都應以相同的單位(上例中的 LSB)表示。
實際上,ADC 只是誤差源之一。其他幾個組件(例如輸入驅動器、電壓基準等)可能會增加額外的誤差,因此必須予以考慮。
審核編輯:湯梓紅
 電子發燒友App
電子發燒友App



















評論