電抗元件如何影響 LC 電路中的相移？詳細了解模擬設計中的相移。

本文將討論相移，即電路導致電壓或電流從其輸入到輸出的超前或滯后的影響。特別是，我們將關注無功負載和網絡如何影響電路的相移。

我們將專門研究相移如何影響完全可靠的運算放大器，以及如何在某些諧振網絡拓撲中使用電抗元件來發揮我們的優勢。

緩沖器上的容性負載

在上一篇文章中，我們了解了如何對電路中電抗元件引起的相移進行建模。現在，讓我們將到目前為止學到的知識應用到運算放大器電路中。

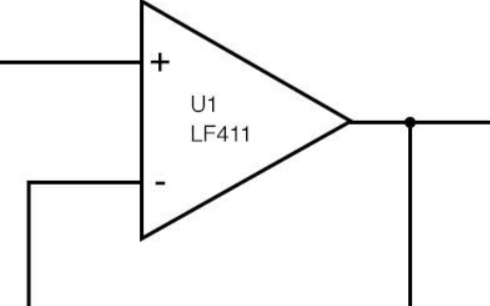
下面是一個用作簡單緩沖器的運算放大器。

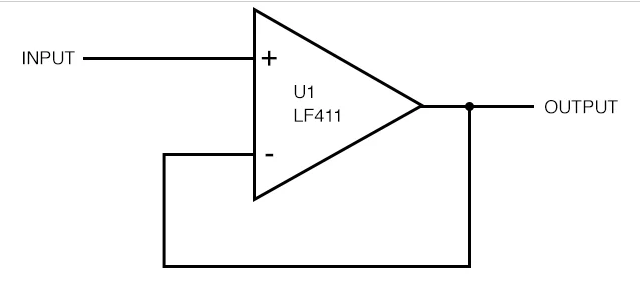
圖 1. 使用 LF411 運算放大器的基本緩沖器或“電壓跟隨器”。

在相位開始下降之前，響應均勻且平坦高達 1 MHz。

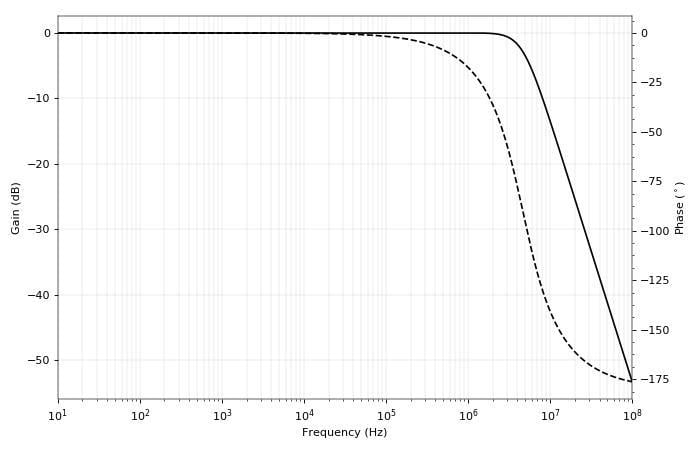
圖 2. LF411 電壓跟隨器的輸出響應。它開始衰減大約 4 MHz 的信號。

該電路依賴于負反饋（同相輸出到反相輸入），-180° 相移導致負反饋變成正反饋（180° 相移輸出到反相輸入）。

現在讓我們嘗試用電容器加載電路。

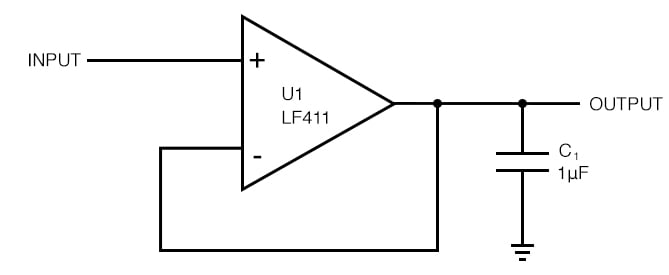
圖 3. 使用緩沖器驅動非常大的容性負載。這不是一個好主意！

如果運算放大器具有阻性輸出阻抗，對于此運算放大器（LF411），單位增益約為 0.1 - 10 Ω，我們預計該電容器會導致高于截止頻率的 -90° 相移。讓我們看看發生了什么。

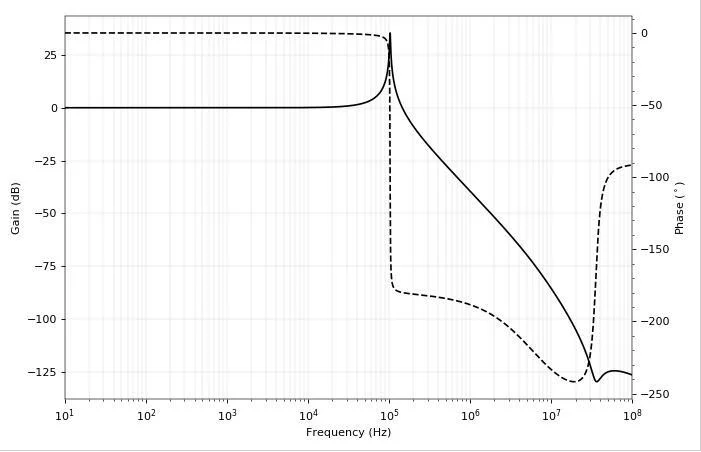
圖 4. 電容問題的證據：放大器開始振蕩！

那看起來很糟糕。振幅響應有一個共振峰值，相位突然下降到 -180°，這是振蕩的完美配方。必須至少有三個電容（電感不太可能）導致這些響應變化。有了我們的嫌疑人，我們就可以遍歷電路并找出到底是什么導致了問題。

使用反應性網絡實現相移

相移在反饋網絡、諧振網絡和振蕩器等電路中變得尤為重要。我們可能希望在我們的電路中有一個 90° 的相移以有意地控制相位。很簡單，我們可以添加一個電容器（或者對于冒險者來說，一個電感器）來分流輸出，看看它能把我們帶到哪里。

事實上，我們可能不希望負載上只有90° 相移。也許我們想要 180°。

也許我們會再放第二個電容器？

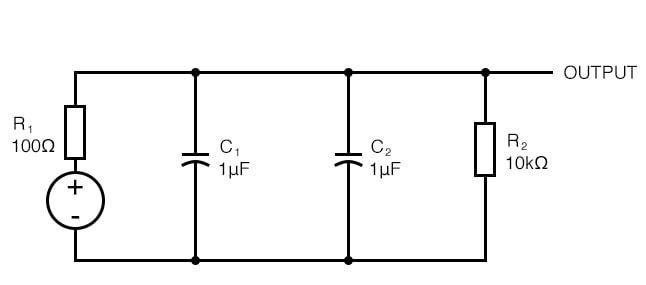
圖 5. 創建 180° 相移的無辜嘗試

那是行不通的——兩個并聯電容器只是形成一個等效電容器。它們都共享相同的電壓，因此它們不能同時貢獻不同的滯后量。我們需要更有創意。

實現這種效果的一種方法是使用多級 RC 濾波器。但更可取的途徑可能是將電容器與一個或多個電抗元件分開，如以下電路所示。

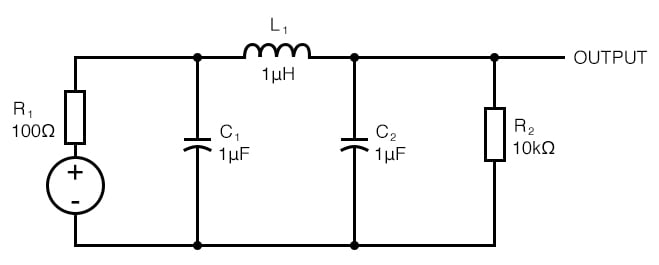
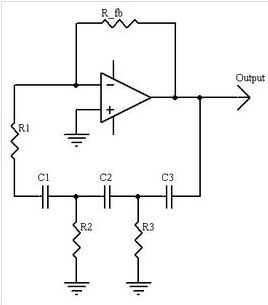
圖 6. 解決這個問題，該電路在諧振時應該有 180° 的相移。

該電路是一個低通濾波器，它將以與由 1 μF 電容器和 0.5 μH 電感器（或 0.5 μF 電容器和 1 μH 電感器）組成的諧振網絡相同的頻率諧振。

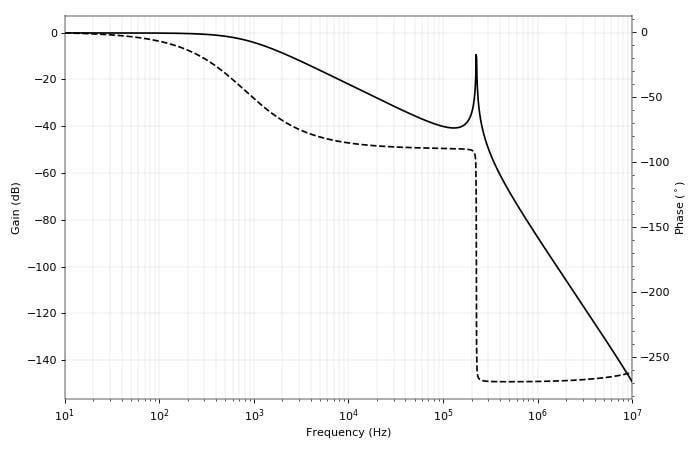
圖 7. CLC 網絡的波德圖顯示良好的共振和快速的相位變化。

從響應和相移我們可以看出，電路的行為類似于 RC 濾波器，源電阻器和兩個電容器并聯，在諧振峰值前不久達到 -90°。然后出現諧振峰，相位驟降至 -270°（三個電抗元件的相移）。恰好在諧振時，相移是所需的 180°。

該電路用作 Colpitts 振蕩器中的諧振元件，電感器-電容器-電感器變體用于 Hartley 振蕩器。通常，電路會繪制成圖 8 所示的樣子。

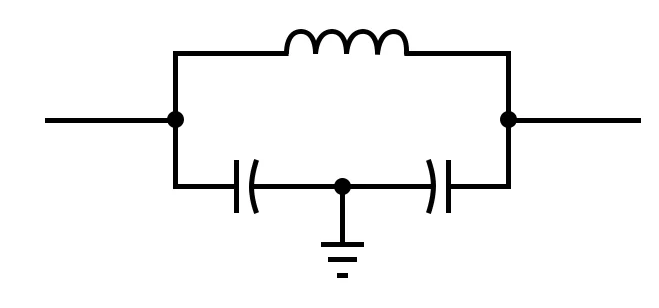
圖 8. CLC 電路的替代圖，經常出現在 Colpitts 振蕩器示意圖中。

雖然它可能會稍微混淆元件的用途，但如圖 8 中所示繪制元件給出了單個諧振元件的外觀。您可以在圖 9 中看到一個帶有以這種方式繪制的諧振網絡的 Colpitts 振蕩器示例。

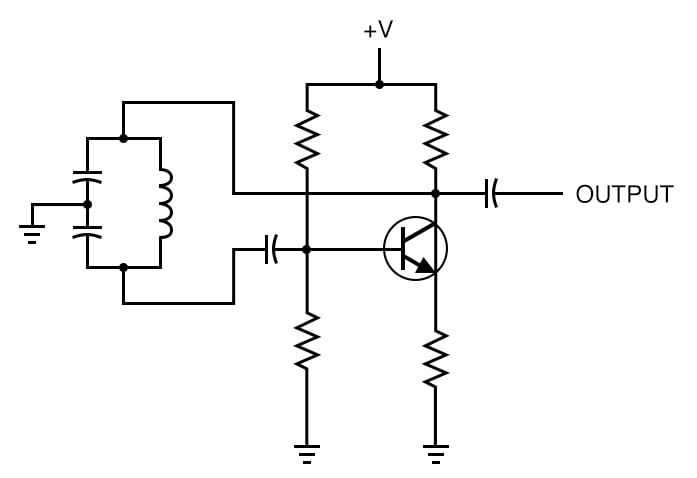
圖 9. Colpitts 振蕩器的典型繪圖

兩個例子引起了一些共鳴。因為諧振元件依賴于電抗元件提供相移的能力，所以多談談諧振電路中的相位將是說明性的。

建模諧振槽

當電感器的電抗與電容器的電抗相等時，串聯 LC 電路諧振。此時，電感和電容共享相同的電流；理想情況下，電感器提供 +90°（超前）電壓相移，而電容器提供理想的 -90°（滯后）電壓相移，這意味著電路末端的電壓為 0° 異相（無壓降、短路）。類似的效果會產生 LC 諧振回路。

但正如我們現在所知，當源或負載阻抗設置正確時，電容器和電感器只能提供 +/- 90° 相移。以這個諧振回路為例。

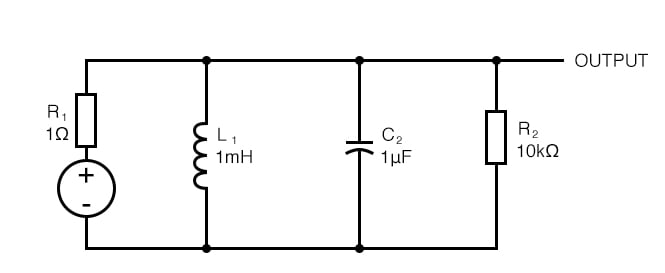
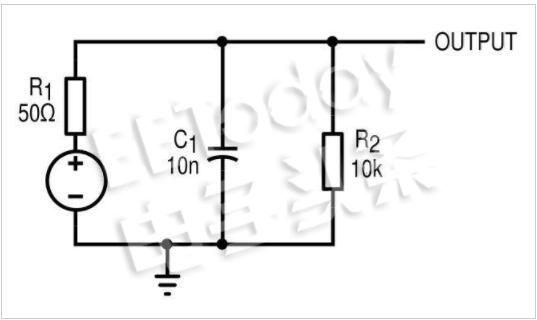
圖 10. 一個簡單的諧振回路，由 1 Ω 輸出阻抗饋電。會響嗎？

源阻抗僅為 1 Ω，負載為 10 kΩ。坦克應該在 5 kHz 下共振。我們可以通過應用輸入階躍并尋找振鈴來測試共振。模擬結果如下。

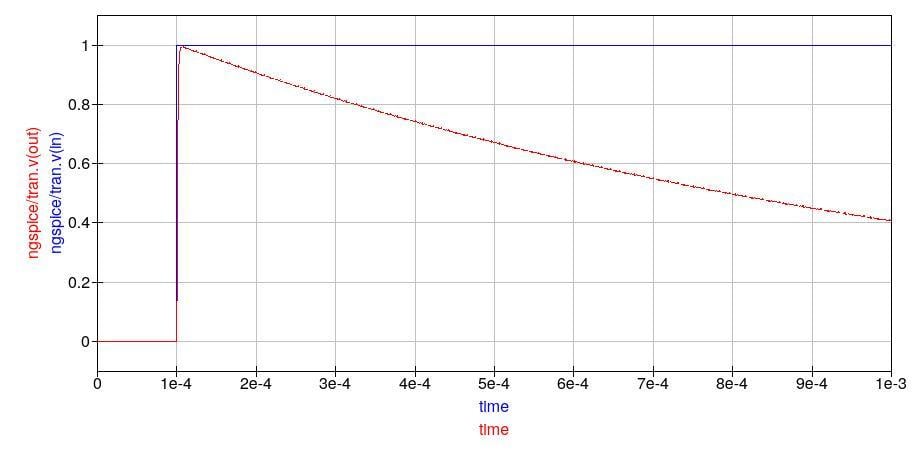
圖 11. 坦克的響應過于衰減，不允許任何振鈴，這在許多情況下是可取的。

坦克似乎并沒有響太多。原因在于源阻抗，鑒于我們的 L 和 C 值，它太低了。我們希望我們的電容器和電感器能夠在諧振頻率下快速來回交換能量，但效果會減弱，因為諧振回路 Q 因數太低。

有幾種方法可以理解這一點。在相移的背景下，我們可能會提出以下解釋。單獨查看源阻抗和電容器，我們發現它們形成了一個截止頻率為 160 kHz 的低通 RC 濾波器。相反，源阻抗和電感器構成一個截止頻率為 160 Hz 的 RL 高通濾波器。

如果我們同意諧振回路的行為取決于組件提供的相移（來自電容器的 -90° 電壓相移，來自電感器的 +90° 電壓相移），那么阻尼的原因就很明顯了。

RC 低通濾波器將提供高于其截止頻率的 -90° 相移，RL 高通濾波器將提供低于其截止頻率的 +90° 相移。回路的諧振頻率 5 kHz 對于 RL 濾波器而言太高而無法提供正相移，對于 RC 濾波器而言太低而無法提供負相移。

以這種方式推理，我們通過改變 L 和 C 的值（同等地降低電感和增加電容）或改變源阻抗來誘使電路產生振鈴。

增加源阻抗具有預期的效果。

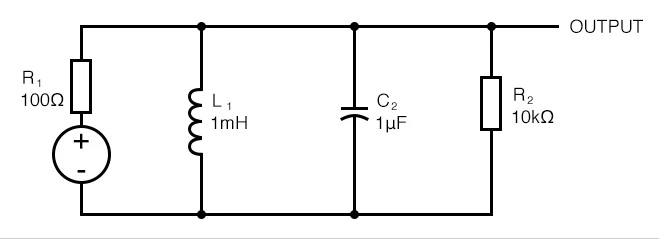
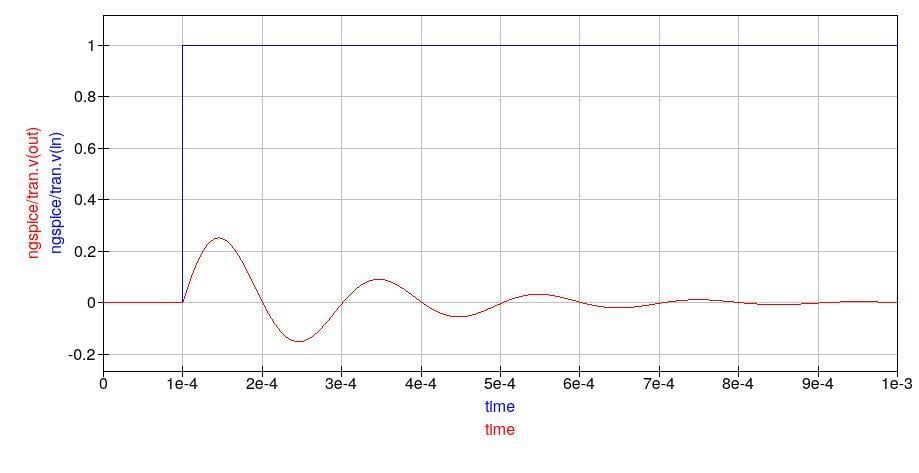
圖 12. 源阻抗為 100 Ω，槽路振鈴頻率為 5 kHz。

現在，正如預期的那樣，槽路振鈴，周期為 0.2 毫秒（對應于 5 kHz 的諧振頻率）。

結論

本文仔細研究了模擬電路中的相移。我們的主題讓我們了解了各種電路：放大器、濾波器、諧振回路和振蕩器。電容器和電感器總是會引起相移，但效果受源阻抗和負載阻抗的影響。在這里，我們主要假設源阻抗和負載阻抗是電阻性的。然而，反應性元素總是存在的。

要分析電路中的電抗元件，我們應該考慮為元件供電的電路的輸出阻抗，以及后續電路的輸入阻抗。現在，當我們希望電路以特定方式運行時，我們可以使用我們對相移的直覺來指導我們，將我們推向正確的方向。