前言

前段時間一直在負責某個項目的debug工作，其中一個問題的核心原因是接收電路的輸入失調電壓過大造成，該接收電路是以op為核心器件構建的信號鏈電路，負責對信號進行放大、均衡等。這次debug經歷讓我對失調有更深入的理解之外，也讓我認識到自己到失調知識的理解是碎片化的，因此這篇文章主要目的是梳理一下個人對失調的理解，爭取有系統性的理解。

作為經驗總結性文章，爭取用通俗易懂的語言來表達。對于總結過程中提到的內容，如果教科書上有詳細介紹的，這里就不再抄書了，畢竟抄書是一件無趣又費時間的事情。此外，為了避免漫無目的地談論一個話題的無效情景，應該聚焦一個話題展開，且這個話題應該圍繞某類具體的電路的來探討失調。這樣的電路不多，我認為選擇運放是一個較好的選擇，這是基于以下幾個原因：

• OP是模擬電路中最常見的電路，工程中出現頻次極高；
• 很多關注失調大小的電路如LDO、ADC等電路，都往往與OP有關；
• OP作為核心電路之一，可獲取的資料最多，便于查閱；
  因此，本文將主要以OP為例分析其失調電壓的影響因素，然后從設計角度給出優化失調的方法。

幾個名詞

在開始之前，有必要對幾個名詞做一番解釋，如“失調”、“失配”、“匹配”等詞。

“失調”和“失配”是兩個很容易混淆的詞匯，雖然只有一字之差，但表達的含義卻完全不同。失配mismatch是芯片工藝加工過程中存在的客觀非理想因素，不管工藝如何先進，失配都是存在的。比如兩個緊鄰的輸入對管，盡管我們設計地一樣，它們的W和L并不會完全一致、每個管子的摻雜濃度也有差異、它們的柵的光滑程度也不一樣。這就像“世界上沒有完全相同的兩片樹葉”一樣，任何你期望達到理想匹配的器件總會帶有瑕疵，這些瑕疵可以稱為“失配”。從這個角度而言，實際制造過程中的偏差以失配呈現在我們眼前。

接下來我們說下“匹配”，因為存在失配，所以我們在版圖布局時，會在物理位置的擺放上思考更多，盡量爭取用更合理的擺放位置來使兩者失配的影響最低。因此就有了諸如書上說的一維匹配、共質心匹配等匹配技術。所以，“匹配”是一種手段，是以物理的方式減弱失配的影響，匹配技術是模擬電路版圖設計藝術性的一個重要體現方面。

“失調則是一個參數名詞，比如有“失調電壓”、“失調電流”等。那么“失調”和“失配”之間存在什么關系呢？答案是：失配是產生失調的充分非必要條件。簡單來說，就是有失配一定產生失調，但有失調卻不一定存在失配（或者沒有失配也有可能產生失調）。

前半句是好理解的，這里解釋下后半句，為什么說即使沒有失配也有可能存在失調呢？就拿簡單的五管運放、電流鏡電路來說，他們首先存在結構性的不匹配，也就是說結構本身就不對稱，對于這種電路，即使不存在失配mismatch，他們也是存在失調電壓的。教科書上對剛描述的情況都有提及，這里不再搬運內容了。總之，這種失調又被稱為“系統失調”，屬于系統誤差，說白了就是結構性不對稱導致的失調，解決這類失調，只要采取對稱結構，就可以消除結構性失調，即消除系統失調。

那對于全對稱結構而言，雖然沒有了系統失調，但失配mismatch仍會導致“不對稱”，這就像前面說的“世界上沒有完全相同的兩片樹葉”一樣，你認為的一樣和對稱只是你認為的。為什么呢？舉一個簡單的例子，假設沒有失配，同樣偏置下的兩個尺寸相同的MOS管，其輸出電流肯定是完全相同的，假設都為a，其輸出電流的差異為0，如果以輸出失配電流來衡量的話，那么此時的失配電流為0，也可以說沒有失調電流。但真實的情況是，一只輸出電流為a,另一只為a+x(x≠0)，這時候有了差異，差異以x大小呈現，此時的失調電流為x。

好了，前言到此結束，接下里開始核心內容。本文將從以下幾個方面進行展開：

• 什么是運放的失調電壓，它是怎么定義的？
• 失調電壓是怎么產生的？
• 一個簡單全差分OP輸入失調大小計算的例子
• 復雜結構的失調計算技巧

什么是運放的失調電壓，它是怎么定義的？

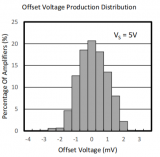
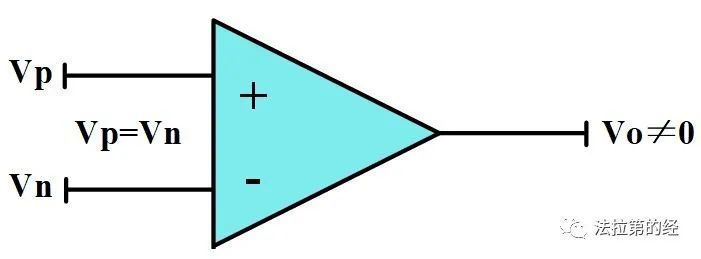
對于一個理想的全差分運放，當差分輸入Vin=0時，其差分輸出Vout=0，然而在實際運放中這是不可能實現的。舉個例子，如果我們有一個真實的運放，當Vin=0時，你會發現其Vout≠0，接著當你慢慢改變Vin的值，終于在某個值，比如Vin=10mV時Vout變為了0，那么此時的Vin值即為運放的輸入失調電壓，一般用Vos表示。也就是說，你手里的這個實際運放的輸入失調電壓Vos=10mV。

也就是說，全差分OP的失調電壓可以這么定義：可以使差分輸出等于0時對應的差分輸入即為失調電壓。

那對于單端運放，失調應該怎么定義呢？書上一般是這么說的：可以使差分輸出等于vdd/2時對應的差分輸入即為失調電壓。這里的“vdd/2”不應該做僵化的理解，其實可以認為是不考慮mismatch時的輸出DC值，它是一個基準值，有失配時輸出肯定不等于基準值，而能令輸出回歸到基準值的輸入即為失調電壓，所以單端運放的定義可以是：可以使輸出等于設定的基準值時對應的輸入即為失調電壓。

失調電壓是怎么產生的？

其實，這個問題在前言部分也有所提及。對于全差分OP而言，失調是因為失配而產生的。我們知道，全差分OP是全對稱的，但在真實的物理世界，尤其是每只管子都是在帶有隨機制造誤差的產線上加工出來的，因此“全對稱”只是理念上的產物，實際是不存在的。

雖然說失配的存在使全差分只在理想上對稱，但這樣的結構在抵抗失配影響方面比起單端電路而言仍然具備極大優勢。雖然說客觀世界上的失配無法避免，但為了做出更優秀的電路，很多人還是為此在不斷努力。這樣的努力是體現在多方面的，比如工藝工程師不斷優化加工精度，減小隨機誤差的影響；IC設計工程師則分析某種電路在參數性能上是如何受失配影響的，他們通過設計更大的W/L、控制管子的驅動電壓或者gm的等方式來盡可能抵抗失配對性能的影響。

其實對作為模擬IC設計師的人們而言，如果選擇通用工藝，那么讓工藝廠在減小失配方面做更大努力是比較困難的，因此主要還是在設計上發力。既然這樣，針對某種常用結構進行失配影響的分析就顯得很有必要了，當我們知道失配對性能的限制之后，我們就有方法通過合理的設計來減小失配的影響。

接下來我們找一個全差分OP來進行失配影響分析。

一個簡單全差分OP輸入失調大小計算的例子

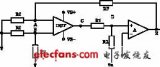
在Razavi的書中，對一個電阻負載的的差分OP進行了失調計算，其結構如下所示：

書上已給出了該結構的Vos,in的計算過程，十分詳細，這里不再抄一遍，畢竟抄書是一件無趣的事情。更有價值的是看到這個計算過程背后的一些思想，它可以給我們帶來關于分析方法上的思考：

• 以 定義作為計算的切入點，即找到一個Vos,in值，使輸出Vout=0；
• 器件不匹配的體現方法：左一半，VTH1=VTH，(W/L)1=W/L, R1=RD,ID1=ID；右一半，VTH2=VTH+△VTH，(W/L)2=W/L+△(W/L), R1=RD+△RD, ID1=ID+△ID；濃縮成一個原則就是：左邊的值=標準值，右邊的值=標準值+△。
• 忽略次要因素，如λ = γ = 0, μnCox的失配；
• 計算過程中將非線性部分，如根式用泰勒近似得到多項式形式，且忽略兩小量乘積項（如△1*△2被忽略），以便得到能夠對設計有指導意義的表達式。

對于上圖所示的運放，將Vos,in的結果整理如下：

觀察上面式（2），負載電阻的失配和晶體管尺寸失配隨驅電壓Vov的增大而增大；而VTH的失配則直接折合到輸入。

對最終公式的的思考：

（1）為了減小Vosin，需要減小Vov，如果電流一定的情況下，則需要增加W/L，假設L保持不變，則需要增加W尺寸，這樣一來Vov減小的同時W/L的失配其實也減小了。我們還知道，閾值VTH失配和W*L成反比，因此閾值失配也會減小。而且，Vov↓同時gm↑，也是實現更低噪聲、更大的增益、更寬的輸出擺幅和共模輸入范圍、更高的CMRR和PSRR所希望的。當然這里也有折中，實際上Vov要與放大器頻率特性相互折衷，例如MOS管自身的本征頻率fT是與Vov成正比的。

（2）RD的失配也是可以考慮減小的。RD一般是工藝電阻，保持阻值不變（即L/W不變）的同時可以考慮同比增大L和W，這樣有益于降低電阻失配。

復雜結構的失調計算技巧

上面的公式（1）是一個很重要的結果，這個結果雖然是從R負載的全差分OP得到的，但對于更復雜的全差分OP的輸入失調計算中仍然會反復利用到該公式，這一點倒并不意外。有些時候我們可以將簡單結構看成是復雜結構的簡化版，或者說復雜結構其實也是從某簡單結構演變而成，本質的拓撲是相同的。從已有結論擴展到復雜結構的計算，無疑可以省卻大量的計算過程。

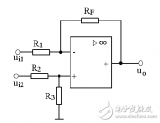
Razavi書上的另一個例子就是電流源負載形式的全差分OP，其結構如下：

計算得到的Vos,in如下

根據公式揭示的信息，在設計上可以按照下面的思路進行失調優化：

• N管Vov取小，W和L可考慮同比擴大。好處：W/L本身失配減小，且受更小的過驅電壓衰減、閾值失配也減小、gmn增大，更有益于衰減負載管失調；
• P管的Vov取小，大括號里W/L失配影響減小，但gmp反而會增加。所以我認為設計時首先可以根據gmn大小選擇gmp的大小，確定gmp/gmn的衰減比。偏置電流一定時，倒推確定P管的Vov，然后盡量選取大的W和L，以直接減小W/L失配和閾值失配。

下面是這個例子的計算背后的一些經驗性思考：

首先，Vos,in包含了所有負載管和對管的失調。書上在計算時，使用到了疊加法的原則，這個原則的應用是十分廣泛的。在這個例子里，在計算輸入對管的失調時，先假定負載管是理想的；等到計算負載管引入的失調時，則假定對管是理想的，最后只需要將計算得到的兩個結果相加即可得到最終結果。能夠應用疊加法的前提是認為負載管的失配和對管的失配是兩個完全獨立的因素，它們之間沒有相互影響。在其他場合要使用疊加法時也需要思考一下這個前提是否存在。

其次，式（3）中Vosn、Vosp是其實直接利用了公式（1）,只是因為應用疊加法的兩次計算中△ID=0，因此這里收過驅電壓影響的因素只有W/L失配。為什么這個例子中計算時認為△ID=0？（顯然和前一個例子不同），這是因為計算對管失配時，負載管是理想的，所以I3=I4，左右兩側電流不存在失配。同樣在計算負載管失調時，輸入對管理想，所以I1=I2，左右兩側電流也不存在失配。

最后，是“折算”的方法。雖然我們能夠計算出負載管失調Vos,p，但需要將其折算到輸入級去。之所以進行這樣的折算是因為我們關注的是輸入參考失調。對于為什么要折算，我有點個人的理解。在實際層面，顯然每個管子的失配最終引起的是輸出結果Vout≠0（當Vin=0時），這時的值為Vos,out。為了在數學形式上的簡介和理想模型的有效性，富有智慧的人們引入了“折算”概念，即將Vos,out除以gain得到Vos,in，稱其為輸入參考失調電壓。這完全是數學的處理。我想人們總要考慮到某些優點才會別出心裁這么處理的，因為這么處理之后，就可以將一個實際OP等效成（或建模成）一個輸入存在Vos,in的理想OP。這么等效之后，在所有其他的計算中，可以將Vos,in與Vin相加得到新輸入Vin,new，而OP仍可以視作理想的。

具體折算時，和噪聲的處理技巧一樣，Vos,p乘以gmp換算為電流，然后再除以gmn等效成輸入電壓，即Vos,p*gmp/gmn。

這篇文章就先到這里。其實在寫這篇文章的過程中，感覺還有很多內容可以寫，比如為什么bjt工藝的失調會比cmos工藝的失調好？更復雜的運放結構在計算失調時應該怎么考慮？一個工藝的失調可以通過什么方式來評估？等等。這些問題爭取在后續的文章中給出回答。