引子

迄今為止，人類歷史上發(fā)生了三次工業(yè)革命。第一次工業(yè)革命開始于蒸汽機的發(fā)明。其核心是將化學能（煤炭）轉(zhuǎn)化為機械能（蒸汽機），人們不再僅僅依賴畜力、水力和風力。

第二次工業(yè)革命則發(fā)端于人們對于電力的深度利用。人們發(fā)明發(fā)電機，電線和電報，這一切都讓能量和信號的傳遞變得更加便捷。另外，更加高效的內(nèi)燃機也開始替代第一次工業(yè)革命中的蒸汽機。

第三次工業(yè)標志著數(shù)字化時代的開啟，人類初步脫離具體的物理媒介的束縛。這時候，照片變成一堆可以傳送的數(shù)字，而不再是一張張具體的膠卷。

由此可見，每次工業(yè)革命都會對我們的生活方式都會產(chǎn)生根深蒂固的影響。我們自然會問，下一次工業(yè)革命會是在什么地方開啟呢？這點很難預料。也許是人工智能，也許是量子技術(shù)，也許是生命科學，又也許在幾十年以后的人們看來，我們現(xiàn)在正處于第四次工業(yè)革命的風口浪尖。

無論如何，在之前的三次工業(yè)革命當中，人類對世界的操控變得越來越精細 —— 從一顆螺絲釘?shù)?a target="_blank">芯片上納米尺度的晶圓顆粒，科技從宏觀邁向微觀的步伐令人嘆為觀止。如果人們對世界的控制突破納米的限制進入更加微小的尺度，那時候，人們面對的又將是一個全新的世界，而那個世界的法律是量子力學（quantum mechanics）。量子技術(shù)正是設(shè)想在量子力學上的全新技術(shù)。也因此，量子技術(shù)很有可能打開下一次工業(yè)革命大門的鑰匙。

什么是量子比特？

量子世界和宏觀世界有著諸多的不同，其中一個便是，量子是可以疊加的。什么意思呢？在經(jīng)典世界里，一個人只能在辦公室里上班，或者在家里休息。而在量子世界里，人們可以處于辦公室上班和家里休息的疊加狀態(tài)。當老板打電話詢問你是否在上班時，你告訴以一定概率告訴他是或者不是。

這時候你可能覺得量子世界和經(jīng)典世界并沒有什么區(qū)別，老板總是隨機地得到兩個不同的答案。這時我們讓老板換一個問題，讓他詢問你是否處于工作和休息的疊加態(tài)A上。在經(jīng)典世界里，除非你有精神分裂癥，否則難以問出這個問題。而在量子世界里，這卻成為一種可能。你可以回答他是或者不是。

現(xiàn)在我們用更精確的數(shù)學語言來陳述。我們用 0 表示工作，1 表示休息。有信息學基礎(chǔ)的讀者都知道，經(jīng)典的信息狀態(tài)（比特，bit）只能是 0 或者 1，所以我們能夠輕易地測量經(jīng)典比特的取值。而量子比特（qubit，為了醒目，下文都用 qubit -- 小編注） [1] 可以是介于 0 和 1 之間的多種選擇，qubit 的每一個狀態(tài)都可以表示成一個單位向量：

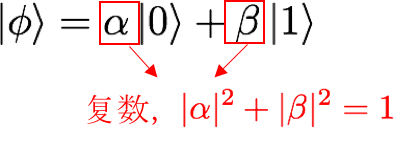
小編旁白

在量子力學中，人們通常使用是物理學家保羅狄拉克發(fā)明的記號?（bra） 和??（ket），其中 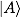?表示量子 A 的狀態(tài)，在數(shù)學上可以看作是一個（有限維或無限維的，定義了內(nèi)積的）向量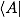； 表示?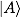?的對偶線性算子，使得???。

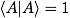在上述框架下，物理量的測量過程總是通過用一個 bra 算子作用在一個 ket 狀態(tài)上來完成的，由于?ket 狀態(tài)允許出現(xiàn)疊加態(tài)，而每個疊加態(tài)都服從某一個概率分布。這和經(jīng)典世界很不一樣，因為在經(jīng)典世界中，每個狀態(tài)都是確定的。

在量子世界中，老板的詢問則意味著對經(jīng)典（或量子）比特進行檢查（或測量），通常通過 “”?作用在 “”?上表示測量的過程。在量子世界中，老板可以選擇不同的問題提問（例如“你是否80%概率在休息20%概率在工作”或“你是否99%概率在休息”這種在經(jīng)典世界看來很奇葩的問題），這意味著他可以選擇不同的基矢進行測量，這在數(shù)學上通常用一組正交基表示。是否上班對應一組基矢

，是否在疊加態(tài) A 又是另外一組基矢，

。

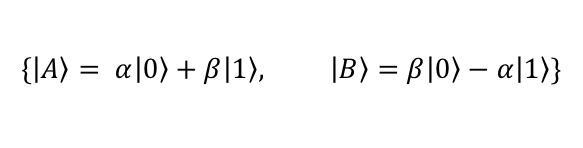
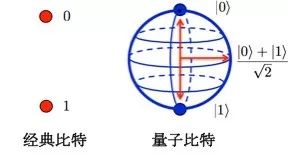
經(jīng)典比特只有兩個取值，量子比特則可以在整個三維球面上取值——小編注

當我們選擇?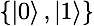?基矢進行測量時，我們得到 0 的概率是?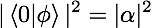?，而得到1的概率則是?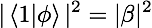?（計算過程本質(zhì)上就是計算向量內(nèi)積）。而當我們選擇?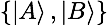?作為基矢的時候，我們得到的答案總是肯定的，因為??。

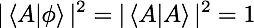講到這里，我們?nèi)耘f忽略了一件非常重要的事情——測量會對 qubit 的狀態(tài)造成影響，這個過程被稱為塌縮（Collapse）。例如，我們選擇基矢 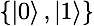?對 qubit? 進行測量，如果測量結(jié)果是 0，那么這個 qubit 就變成?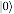?。類似的，如果我們選擇基矢? 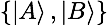進行測量，測量結(jié)果為 A 意味者這個 qubit 塌縮到?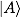?, 而結(jié)果 B 則意味者 qubit 塌縮到?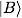?上。?

現(xiàn)在讓我們利用量子塌縮來做一個偵測器。假設(shè)我們要出門旅行，所以在房間里放了一個qubit 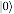。如果有小偷進入這個房間，這個 qubit 就會在 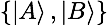?基矢上進行測量。那么這個 qubit 就會變成 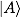?或者 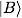。不管測量結(jié)果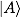是? 還是 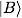, 這時候我們再次對 qubit 在老基底 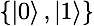?上進行測量，它都有一定概率輸出1。所以等我們回來以后，我們就對 qubit 在老基底?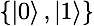?上進行測量，如果測量結(jié)果是 0，那么我們認為沒有小偷；如果測量結(jié)果是 1，那么我們認為有家里被小偷光顧過了。

有的讀者可能會懷疑這個方案的可行性，因為無論有沒有小偷光顧，都有一定概率輸出 0，所以我們還是有一定概率誤認為小偷沒有來過。這個時候我們把裝置改進一下 —— 我們放很多個 qubit，在旅游歸來之后，對所有 qubit 都進行上述測量。如果有一個qubit輸出1，那么我們就認為小偷來過了。因為我們有很多個 qubit，所以誤認為小偷沒有來過的概率低到可以忽略。

這個量子探測器乍看起來似乎有些雞肋，因為我們需要投入很多 qubit。不過事實上整個過程卻隱含著量子密鑰分發(fā)方案 BB84 的核心。

神奇的量子加密技術(shù)

現(xiàn)在讀者們已經(jīng)對是 qubit 有了一個初步的映像，接下來我們介紹量子加密技術(shù)。

在雙方通信的過程中，總難免會有第三方想去竊取通信過程中的信息，而加密技術(shù)的出現(xiàn)就是為了防止信息被竊取。加密（encryption）的含義是把我們希望傳送的信息，稱為明文，通過某種算法（稱為加密算法）把明文變成一串只有接收方才能理解的信息，這個信息稱為密文。

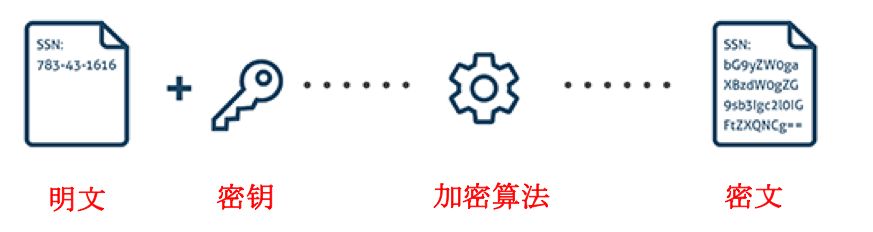
加密過程

這個世界上的加密方式有很多，他們的安全等級也不一樣。很多密碼都是有條件安全的，比如假設(shè)第三方只擁有有限的計算能力。我們知道的大規(guī)模商用的 RSA 密碼是這樣的一種安全級別。這種加密算法的安全核心在于，基于大素數(shù)分解的數(shù)學問題是困難的，目前沒有行之有效的算法（更專業(yè)地講，所有算法都是指數(shù)時間的——小編注）。要想攻破這個密碼，就必須攻克這個長久以來困擾數(shù)學家的素數(shù)分解問題。

然而遺憾（對于不法之徒而言，幸運）的是，量子計算機可以有效地解決素數(shù)分解問題，這也意味著 RSA 密碼體系在量子計算機面前并不安全。更高一個級別的安全性是無條件安全，也就是說，就算擁有無窮的計算能力也無法攻破這個密碼體系。

讀者們可能懷疑如此夢幻的加密體系也許真如黃粱一夢，根本不存在。事實上早在上個世紀初，人們就提出了一次一密算法（One-time pad），并且證明了他是無條件安全的。不過看似如此夢幻的算法卻沒有被普及開來，因為它有一個嚴重的缺陷。經(jīng)典的加密方式要求通信雙方在通信之前共享一串和明文是等長的比特串，通常被稱為密鑰。密鑰就像是一把鑰匙，在加密的過程中，我們就好比把明文塞進了一個保險盒，然后用密鑰把它鎖上。接下來我們把盒子送到接收方手里（可以大搖大擺地送過去），并用自己手里的密鑰打開盒子，取出想要的信息。一次一密算法要求密鑰和明文的長度相同，這就讓這個加密過程變得極其昂貴，難以被商業(yè)化。

量子加密技術(shù)的創(chuàng)新點在于密鑰分發(fā)技術(shù)（ Key distribution），它很好地解決了一次一密算法中密鑰生成的難題。此外，物理學家和數(shù)學家證明這個分發(fā)密鑰的過程在理論上是無條件安全的（據(jù)筆者所知，這應該是唯一一個在理論上被證明無條件安全的密鑰分發(fā)方案。）。

為了讓讀者更好地理解量子加密技術(shù)，我們介紹 BB84 方案 [2]，它是由 Bennet 和 Brassard 等人在1984年提出的。BB84 方案的一大優(yōu)點是它不需要量子糾纏，因為量子糾纏是一種比較昂貴的資源。潘建偉院士在 2017 年用墨子號衛(wèi)星實行洲際間的量子密鑰分發(fā)方案也正是 BB84 方案 [3]。?

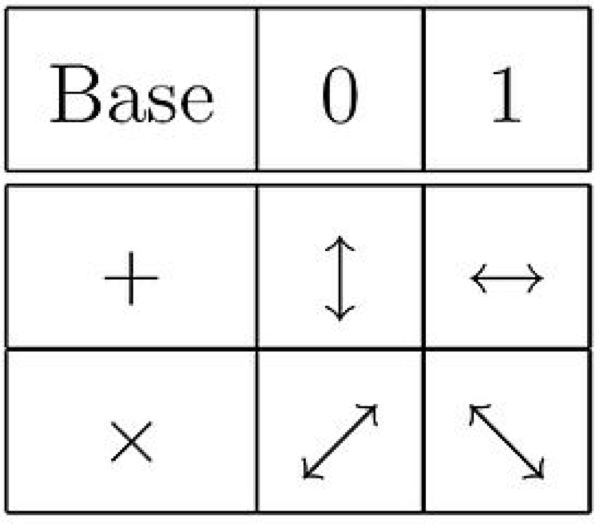
BB84 方案的具體的過程可以從下面這幅圖里看到：

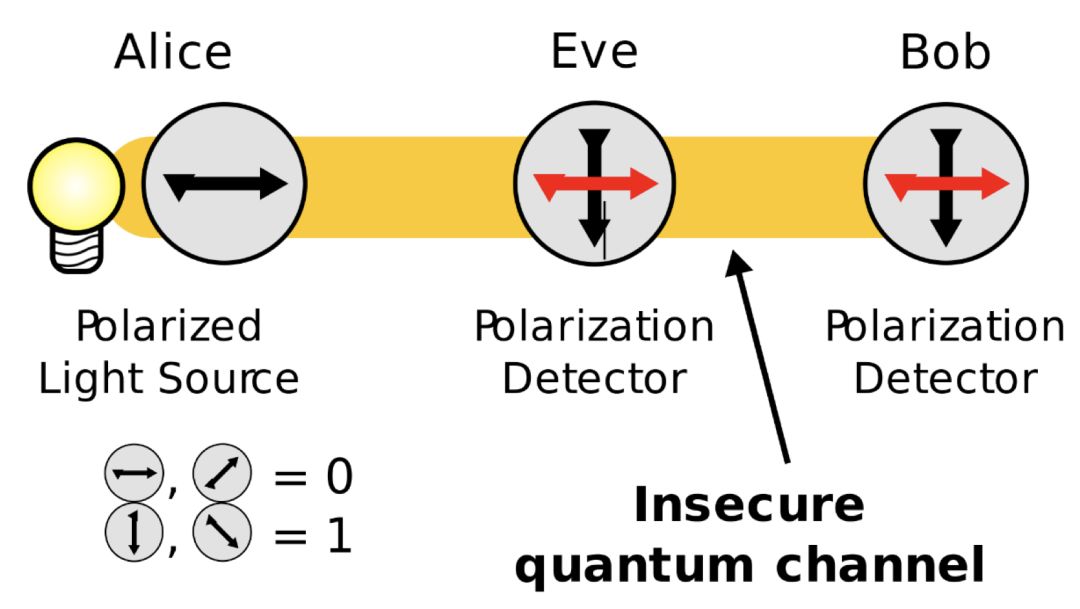
就好比光的偏振一樣，量子密鑰圖片來自維基百科

上面的箭頭只是用以類比光的偏振方向，并沒有嚴格的定義。對于這幅圖的解釋如下（Alice 和 Bob 是信息學領(lǐng)域的常見虛構(gòu)人物——小編注）：

算法——?BB84 量子加密方案

Alice 隨機生成一串經(jīng)典的比特串。接著，對每一個比特 0/1，她又隨機地選擇基矢 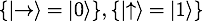?或者??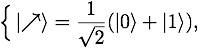???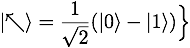，并發(fā)送相應的 qubit?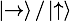?或者?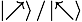。例如，Alice希望發(fā)送信息 “1”給 Bob，如果她隨機選擇了第一組基矢?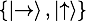，那么 Alice 就發(fā)送量子態(tài)?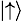?給 Bob。如果 Alice 隨機選擇的基矢是第二組基矢?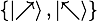，那么她發(fā)送給Bob的量子態(tài)就是?。

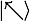同樣的，對于接收到的每一個 qubit, Bob 隨機地選擇基矢 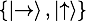?或者?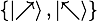?進行測量，他也得到一串經(jīng)典的比特串。值得注意的是，如果 Bob 選擇和 Alice 一模一樣的基矢，那么 Bob 會得到和 Alice 相同的比特串。例如，Alice發(fā)送??給 Bob，Bob 選擇基矢 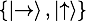?進行測量，那么他總會以概率??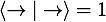?得到測量結(jié)果 →， 這就代表經(jīng)典的比特 1。

Alice 和 Bob 再通過公開的經(jīng)典信道比對各自選擇基矢。如果對于某個 qubit，Alice和 Bob 選擇的基矢相同，那么他們雙方就保留對應的比特，否則就刪除。在基矢相同的情況下，Bob 測量的結(jié)果和 Alice 希望發(fā)送的目標是一致的，此時雙方可以放心保留測得的信息。如果 Alice 和 Bob 選擇的基矢不相同，那么 Bob 有 50% 的概率得到和 Alice 不相同的結(jié)果，此時不管 Bob 測量的結(jié)果正確與否，雙方都放棄這個測量結(jié)果。

Alice 和 Bob 將篩選后的部分經(jīng)典的比特串進行比對，以此確定是否有第三方竊聽。由于 qubit 是無法克隆的，所以第三方 Eve 只能對 Alice 發(fā)送的量子bit進行測量。然而這個測量過程是會破壞測量 Bob 的測量結(jié)果。在沒有第三方竊聽的情況下，如果 Alice 和 Bob 選擇相同的基，那么他們得到的經(jīng)典bit串應該是一致的，否則就是有第三方在竊聽。在這種情況下，Alice 和 Bob 就放棄密鑰，進行重新分發(fā)。

科學家們?nèi)栽谂μ岣呙荑€分發(fā)的速度同時希望降低分發(fā)過程的成本。目前來說，量子密鑰是為數(shù)不多的幾個的開始商業(yè)化的量子技術(shù)之一。

對量子技術(shù)的思考

人們會對量子技術(shù)有各種各樣的批評。其中一些人為量子密鑰分發(fā)是不必要的，因為量子計算機還沒有被造出來。退一步說，即使有了量子計算機，人們?nèi)耘f可以使用相對應的經(jīng)典密碼去對抗量子計算機。

筆者本人不太贊同這些觀點。首先，我們不可能等到量子計算機造出來后才開始研究量子密碼；即使我們可以使用更加高級的經(jīng)典密碼去對抗量子計算機，量子密鑰也未必沒有優(yōu)勢，畢竟用高級的經(jīng)典密碼會消耗更多計算資源也會抬升加密的成本。如果量子密鑰的成本比高級經(jīng)典密碼低，那么量子密鑰將存在很大的商業(yè)前景。

無論如何，量子技術(shù)的發(fā)展可以看成是人們希望理解和操控微觀世界的一種嘗試。而量子密鑰分發(fā)是我們現(xiàn)階段能想到的一個應用方案。不管量子密鑰分發(fā)最后能否帶來巨大的商業(yè)價值，它總是人們邁開利用量子技術(shù)的重要一步。

參考文獻

[1]? M. A. Nielsen and I. L. Chuang,(2007).

[2]? C. H. Bennett and G. Brassard, Proc.1984 IEEE Int. Conf. Comput. Syst. Signal Process. 175 (1984).

[3]? S. K. Liao, W. Q. Cai, J. Handsteiner,B. Liu, J. Yin, L. Zhang, D. Rauch, M. Fink, J. G. Ren, W. Y. Liu, Y. Li, Q.Shen, Y. Cao, F. Z. Li, J. F. Wang, Y. M. Huang, L. Deng, T. Xi, L. Ma, T. Hu,L. Li, N. Le Liu, F. Koidl, P. Wang, Y. A. Chen, X. Bin Wang, M. Steindorfer,G. Kirchner, C. Y. Lu, R. Shu, R. Ursin, T. Scheidl, C. Z. Peng, J. Y. Wang, A.Zeilinger, and J. W. Pan, Phys. Rev. Lett. 120, 30501 (2018).?

編輯：黃飛

?