引言

　　設計在現實世界中運行的電路具有一定的挑戰性。僅僅使電路設計符合規范目標是遠遠不夠的，精確地預測一定范圍條件下電路的表現也很重要，包括各組件的真實值變化。此過程通常稱為電路良率分析。一旦較好地了解了這種表現，設計人員便可以有效地利用預計的制造容差來選擇電路和組件進行設計。

　　眾所周知，正常運行的電路，即使電路參數發生變化，其構建、測試和支持成本也相對較低。

　　本文闡述了容差的使用，以進行良率分析預測，即有多少以不同組件值構建的電路能夠符合規格要求。要想進行有效的良率分析，您必須要擁有：

　　* 較好的電路模型，包括重要組件、雜散等。

　　* 較好的預計組件值變化模型

　　* 通過/未通過的定義或規格

　　利用這三種輸入，您可以進行一些必要的計算，來預測電路良率。用于進行這些計算的工具其效用各不相同，取決于問題的復雜程度和您的洞察力。下面表1中，對一些方法進行了總結。

　　表1. 良率分析方法

?

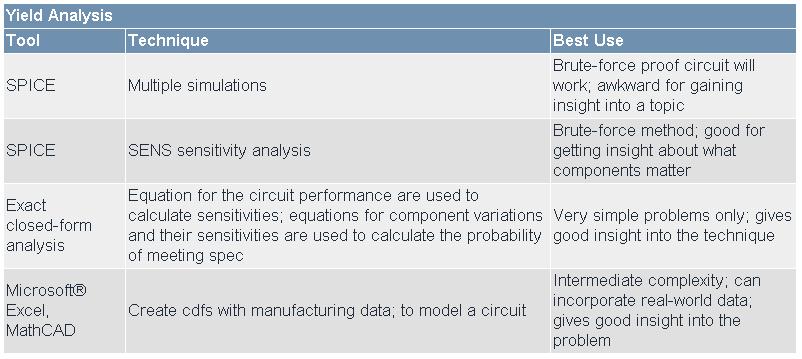
　　本文將介紹如何使用Microsoft Excel軟件進行良率分析，討論了一些諸如概率分布函數(pdf)之類的基本良率分析概念，闡述了如何生成隨機組件值，得到理想的概率分布。

　　利用組件值及設計方程式確定良率

　　電路由各組件組成。這些組件共同組成電路，其整體表現遵循某種規則或設計方程式。要進行良率分析，設計人員必須了解組件值變化和設計方程式。

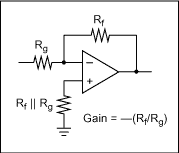
　　例如，就下面圖1所示的簡單增益電路而言，已知RF和Rg的電阻后(假設為一個理想的運算放大器)，就可以很容易地計算出該運算放大器的增益。然而，在現實世界中，如果我們構建該電路數百次，組件Rf和Rg在每次電路構建時的值會有所不同。接下來當對該電路進行測試時，會發現其增益在每次電路構建時也各不相同。在該示例電路中，發生組件值變化的是電阻容差。增益的設計方程式為：

　　增益 = - Rf/Rg

　　例如，如果我們選取Rf = 1kΩ并且Rg = 1kΩ，則增益為-1。

?

　　圖1. 反相運算放大器示例

　　最后，該電路的規格可能會為：增益 = -1 ± 0.1V/V。

　　組件PDF和CDF

　　通常設計人員無法預測某個組件將會出現的值。但是憑借經驗，我們可以預測有多少組件或者多少次產品運行會出現某種表現。對于這種表現的描述稱為一個pdf或者概率分布函數。

　　pdf是一種描述隨機變量X的可能取值x與某個特定值出現概率對比關系的曲線或函數。例如，在本文的示例電路中，我們描述了Rf電阻值與一批電阻中出現該電阻值概率的對比關系。

　　cdf為累積分布函數，為隨機變量X取一個小于或等于某個值x的概率。也就是說，如果我們擁有pdf分布，就可以利用積分計算出cdf。您可能已使用了高斯或正態pdf，其由兩個參數定義：平均值(中心值)和標準偏差(約等于峰值寬度)。圖2描述了正態分布的pdf和cdf。

?

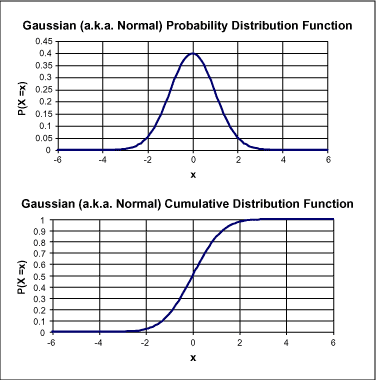
　　圖2. PDF和CDF示例

　　正態分布適合于許多現實世界情況，并且更易于數學實現。但是，請注意!正態分布可能沒有描述出您的某種特殊情況。例如，如果您正使用20%容差的電阻，您會發現5%的電阻被全部去除，并被出售給其他人。這種情況下實際的pdf如圖3所示。

?

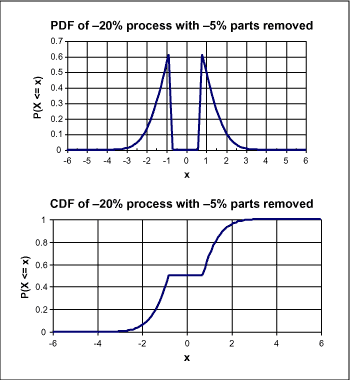
　　圖3. 分類各部件的分布情況

　　利用這種分布，測定電阻值與電阻標簽一致的概率為零!同具有正態分布組件值的電路相比，您的電路會表現得相當差。另外，獲得5%電阻的設計人員會發現其工作比預計的情況要好，因為他的分布對尾數進行了取舍。

　　我們從中得到的經驗是，有許多有用的分布可供選擇，而如何選擇這些分布非常重要。不要把自己局限于正態分布這一種。

　　在Excel中產生隨機組件值

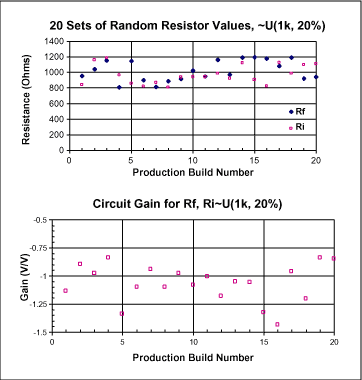
　　如果我們能夠生成一系列隨機數，那么我們就可以用這些數值來代表生產中的電阻值。然后，我們可以用這些值和電路方程式一起來確定電路的增益，將其與規范要求相對比，并計算出良率。下列各圖給出了具體的結果。就20次構建、±20%的增益規范而言，良率為80% (每次運行的結果會略有不同)。

?

　　圖4. 生成隨機電阻值以及得到的增益

　　上面的分析中，每個電阻均使用了一種均勻分布隨機變量。這種均勻分布下，取兩個極限值之間任何電阻值的概率都一樣。您可以在Excel*1中使用兩種方法來生成電阻值：選擇Tools Data Analysis Random Number Generation，或使用RAND()函數(請參考Excel中的RANDBETWEEN())。如果您使用RAND()或RANDBETWEEN()函數方法，電子表格軟件每次計算便重新產生一個值(按F9鍵)。

　　RAND()給出的是大于等于0并且小于1的隨機數。如需獲得大于等于1并且小于b的隨機數，請使用RAND() × (b-a) + a。RANDBETWEEN(a,b)給出的是一個大于等于a并且小于等于b的整數(假設a和b均為整數)，如果a和b是非整數，RANDBETWEEN(a,b)將得到介于a和b之間的一個整數值。

　　不幸的是，大多數組件均遵循均勻分布以外的分布。但是，這類分析在估計最差性能時較為快速和有效。

　　正態分布PDF和CDF

　　Excel提供了大量其它函數，可以幫助我們生成更為真實的pdf。為了生成一種正態或高斯曲線，我們使用了內置函數NORMDIST()。例如，對于平均值 = 0并且標準偏差 = 1的正態分布而言，“=NORMDIST($A7,0,1,FALSE)”返回x = 存儲于單元格A7的概率。

　　標準偏差(通常被稱為Σ)描述了pdf函數峰值的寬度，并相當于第二個導數改變標志的點。這就是用于生成圖2所示pdf的方法。通過將“FALSE”改變為“TRUE”，您將會得到cdf的各個值。

　　如果您沒有更好的數據，那么就假設組件的規定百分比容差為±3標準偏差。例如，一個±10%部件會具有±10/3 = ±3.33% (標稱值)的標準偏差。

　　盡管cdf和pdf正確地描述了正態隨機變量，但是它們不生成隨機組件值。理想狀態下，我們會喜歡使用像“RANDNORM()”這樣的函數，其返回的隨機數字符合正態分布。

　　生成正態分布隨機數

　　如上所述，Excel沒有提供RANDNORM()函數，但是一些附加函數提供了這種必要功能。要想生成10個1kΩ標稱值并具有±20%生產取值范圍的電阻值，請遵循以下步驟：

　　1. 平均數 = 1kΩ標稱值，標準偏差為1kΩ的±20%除以3 = ±200/3 = ±66.67Ω。

　　2. 使用內置函數生成一個數列，選擇Tools Data Analysis Random Number Generation。對話框如圖5所示。

?

　　圖5. 隨機數生成對話框

　　請注意，步驟1中計算得到了平均數和標準偏差。輸入數字10，表示想要生成的隨機數(值)個數。輸出范圍給出了Excel將計算值放入電子表格的單元格。輸出結果如圖6所示。

?

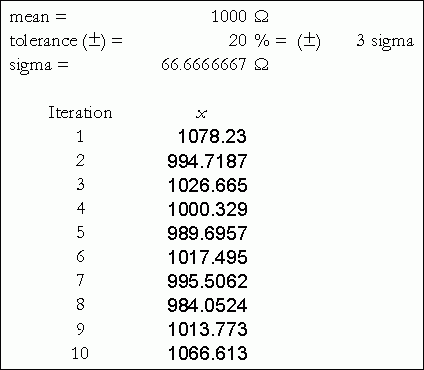
　　圖6. Excel生成的隨機組件值

　　其它有用的內置分布

　　您可能已經注意到，在Tools Data Analysis Random Number對話框中，Excel為您列舉出了許多種分布供您選擇。這些分布包括正態分布、均勻分布、二項式分布、伯努利分布、離散分布以及其它幾種分布。前面所述的均勻分布是一種估計最差性能的簡單、有效的方法。二項式產生一種只有2個值(例如：1和0)的分布，其常見于邏輯電路中。一本好的統計學書籍和一些實驗可以幫助您選擇一種正確的分布。

　　如果您的分布同可用的分布都不匹配怎么辦呢? 制作屬于您自己的隨機數生成器!我們將在下一節中對此進行介紹。

　　生成與生產數據相匹配的隨機數

　　有時，沒有一種內置或標準pdf函數適合于您電路的情況。此外，在分類電阻情況(參考圖3)中所看到的那樣，非標準分布的影響極其明顯。

　　這種情況下，我們會想要繪制一種分布、利用生產測試數據創建一種分布或者使用計算數據創建一種分布，然后生成符合這種分布的隨機數，以進行良率分析。

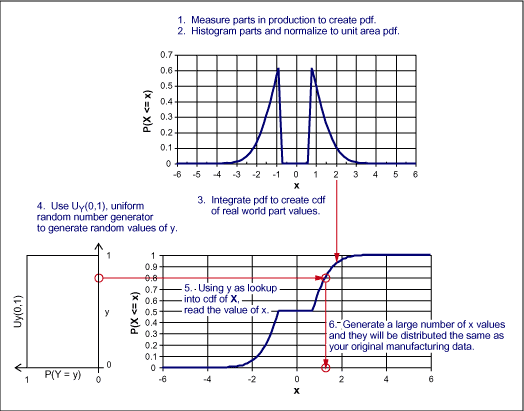
　　創建此類分布以及相應的隨機數需要如下幾個步驟(如后面圖7所示)。

　　1. 測量大量的真實組件或者通過計算來生成數據。您也許能夠從進貨檢查過程獲得這種數據。這種原始數據將被用于創建pdf。

　　2. 將數據制作成柱狀圖，并根據采樣總數進行標準化。換句話就是說，所有概率的和為1。這種標準化的柱狀圖便是我們所希望的隨機數遵循的pdf。

　　3. 對該pdf求積分創建cdf。確認單調達到最大值1。

　　4. 生成一個介于0和1之間的均勻分布隨機數：y~UY(0,1)。

　　5. 將該均勻分布隨機數用作cdf上y = P(X ≤ x)時cdf的指數，并記下x的值。

　　6. 重復步驟4和5，生成所有您需要的x隨機值。

?

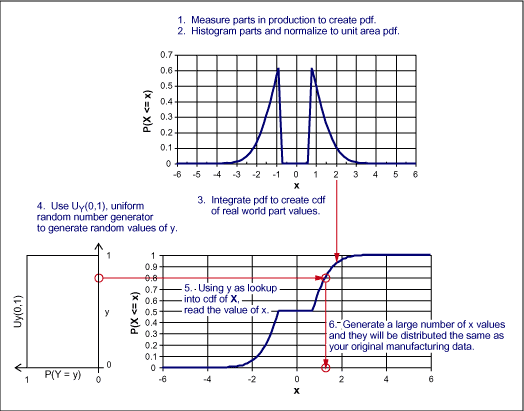
　　圖7. 生成同生產數據相匹配的隨機數

　　結論

　　本文中，我們了解了如何生成良率分析所使用的隨機組件值。對于許多常見分布來說，Excel提供了一些讓這一過程更加快速、簡單的內置函數。對一些特殊情況來說，本文介紹了一種利用均勻分布隨機數和測定cdf來生成任意分布隨機數的簡單方法。