?

　　1、簡介

? ? ? ? 在變壓器差動保護中，如何區分勵磁涌流與內部故障電流是一個固有的、不可回避的難題，多年來一直成為研究的熱點。

　　現在實際運行的變壓器差動保護，主要是采用以二次諧波制動原理和間斷角原理來判別勵磁涌流，其中二次諧波制動原理應用最為廣泛。但是由于CT飽和，無功補償用的并聯電容或超高壓長輸電線分布電容的存在，使得變壓器發生內部故障時也會產生很大的二次諧波，而且隨著大型變壓器鐵心采用冷軋硅鋼片后，飽和磁通倍數由1.4降至了1.2~1.3，甚至低至1.1~1.15，使勵磁涌流的二次諧波含量有時低至10% 以下，這樣二次諧波制動原理的制動比很難選取，保護就可能存在不正確動作;基于間斷角原理的勵磁涌流識別方案也存在著受CT傳變影響等問題[1~4]。其他有代表性的鑒別勵磁涌流的方法有波形對稱原理、波形疊加原理、波形相關性分析法和波形擬合法。實際上，由于三相變壓器勵磁涌流的波形特征隨系統電壓和等值阻抗、合閘初相角、剩磁大小和方向、繞組接線方式和中性點接地方式、三相鐵心結構、鐵心材料和組裝工藝、磁滯回線和局部磁滯環等不同而改變，所以任何以勵磁涌流波形特征為依據的防止由勵磁涌流而引起誤動的措施均不能保證變壓器差動保護不誤動，差別僅是誤動次數的多少[5]。

　　不依賴于勵磁涌流波形特征的方案有：磁通特性識別法[6]，等值電路參數鑒別法[7]。這兩種算法的不足在于都需要預先計算變壓器漏感參數，而且整定困難，其應用前景取決于理論上的進一步突破[5]。本文利用變壓器的原始正常模型，推導出了動作方程，并提出了保護判據。動模實驗數據驗證了該方案的正確性和可行性。

　　2 基本原理

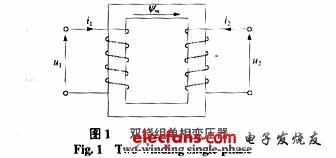
　　如圖1所示的雙繞組單相變壓器，下面的關系成立[8]：

?

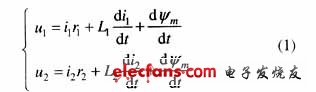
　　式中 U1、U2為一、二次繞組的電壓;I1、I2為一、二次繞組的電流;L1、L1為一、二次繞組的漏感;R1、R2為一、二次繞組的電阻;Ψm為一、二次繞組的互感磁通。

　　設變壓器的變比為NT=1。將式(1)中的DΨm/Dt消去得

?

?

　　由于式(2)是根據變壓器正常運行的模型得到的，所以它適合于外部故障、勵磁涌流及過激磁情況。只有內部故障時，由于變壓器模型本身的內部結構參數發生了變化，它才不再成立。因此，可以通過判別式(2)是否成立，來決定保護的動作行為，因而，在勵磁涌流、過激磁、外部故障情況下保護不會誤動作。下面分別推導兩繞組和三繞組變壓器的動作方程，并根據其動作方程提出了保護判據。

　　3 動作方程的推導

　　3.1兩繞組三相變壓器的動作方程[9]

　　由圖2所示的Y/?接線的三相變壓器，根據電路原理可得到

?

?

　　側繞組各相的漏感;R為?側繞組各相的電阻;R為Y側繞組各相的電阻;Ψa,Ψb,Ψc,為兩側繞組的互感磁鏈。

?

?

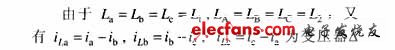
　　側可測的各相電流，所以可將式(3)和式(4)中的等式分別兩兩相減，再進行合并，并歸算到Y側，可得

?

　　由于變壓器制造廠家一般只提供變壓器的短路電抗Xk，并不提供各側繞組的漏感L1,L2，可以利用關系式

代入式(5)，可得

?

?

?

　　在變壓器正常運行(包括產生勵磁涌流和外部故障)時，式(6)中的3個等式成立，而且3個等式中的L2應為同一值;只有變壓器發生內部故障時，式(6)中的3個等式不成立，越嚴重的故障等式兩邊的差別就會越大，并且分別利用3個等式計算出的L2也會有較大差別。這是制定兩繞組變壓器保護判據的依據。

　　3.2三繞組三相變壓器的動作方程

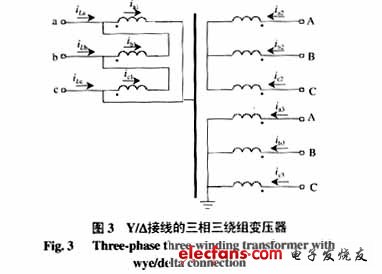
　　下面以Y0 / Y /?-11接線的三繞組變壓器為例推導動作方程，變壓器接線圖如圖3所示。

?

　　對單相繞組有：

?

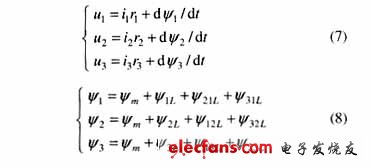
　　式中 R1,R2,R3為1、2、3側繞組的電阻值;Ψ1,Ψ2,Ψ3分別為穿過1、2、3側繞組的總磁鏈;Ψm為穿過1、2、3側繞組的公共磁鏈;Ψ1L,Ψ2L,Ψ3L分別為1、2、3側繞組產生的除Ψm以外的漏磁鏈;ΨijL(I≠J)為第I個繞組產生的除Ψm以外的和第J個繞組交鏈的漏磁鏈。

　　由式(7)、(8)可得A、B、C三相的關系如下：

?

?

?

?

?

　　為變壓器廠家提供的變壓器各側的電抗(歸算到第1側)。

?

　　4 保護判據

　　根據上面的推導，可以分別制定兩繞組和三繞組變壓器的保護判據。

　　(1)兩繞組變壓器的保護判據

　　判據1：當差動電流大于門檻值時，利用L2的估算值，計算式(6)中的3個等式兩邊的差值，如果等式兩邊的差值超過門檻值，判定變壓器發生內部故障，保護跳閘。由于L2的估算值與實際值存在著誤差，故此判據的動作門檻值要躲過勵磁涌流和外部故障時方程兩側的差值，它能夠保證在發生較嚴重的內部故障時保護正確動作。

　　判據2：當差動電流大于門檻值時，利用式(6)計算3個方程中的L2，如果3個方程分別計算出的L2之間的差值超過門檻值，判定變壓器發生內部故障，保護跳閘。此判據可在判據1的基礎上進一步判別變壓器的輕微故障。但在內部相間短路時，由于差動電流數值很大，計算出的3個L2數值會較小，識別其差值較困難。

　　因此，判據1用來識別嚴重內部故障，判據2用來識別輕微內部故障，兩者相結合就會達到很好的效果。

?

　　的6個方程等式兩邊的差值，如果等式兩邊的差值超過門檻值，判定變壓器發生內部故障，保護跳閘。由于

的估算值與實際值存在著誤差，故此判據的動作門檻值要躲過勵磁涌流和外部故障時方程兩側的差值，它能夠保證在發生較嚴重的內部故障時保護正確動作。

?

?

　　同樣，判據1用來識別嚴重內部故障，判據2用來識別輕微內部故障，兩者相結合會達到很好的效果。

　　5 動模試驗及結果

　　5.1 動模試驗系統

　　為了驗證上述方法的正確性及可行性，通過動模試驗獲得了大量變壓器在各種運行狀態下的真實數據，在此，用這些數據對保護判據進行驗證。

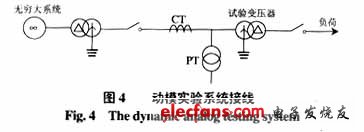
　　動模試驗系統接線如圖4所示。

?

　　在此系統中的試驗變壓器為三單相變壓器組Y,D11，單相變壓器的參數分別為：額定容量10kVA;低壓側額定電壓380V;低壓側額定電流25.3A;高壓側額定電壓1000V;高壓側額定電流10A;空載電流1.45%;空載損耗1%;短路損耗0.35%;短路電壓9.0%~15%。在進行數據錄波時，每個采樣周期采20個點。

　　5.2 試驗結果

　　用動模試驗中獲得的數據來驗證此方法的正確性，每種運行狀態的數據分別測取10次。根據兩繞組變壓器的判據1，得到表1所示結果。

?

　　表1中的差值是10組數據差值綜合結果，在計算中將L2估算為 (Xk/W)/2。由表1可以看出，設判據1中差值的門檻值定為20，那么，除了輕微匝間故障無法識別外，其他故障均能夠可靠地識別。

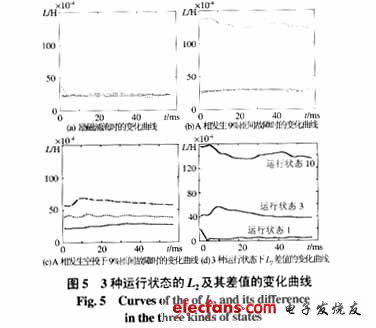
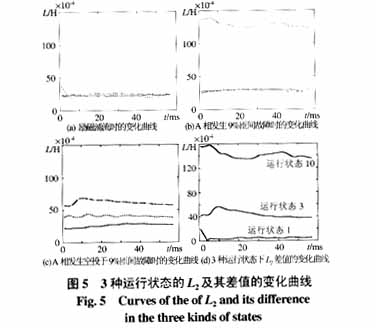
　　判據2可以對輕微匝間故障進行識別，下面依據判據2對表1中序號為1，3，10的3種情況進行判別。圖5(A)、(B)、(C)是將動模試驗數據代入到式(6)中，計算得出的3個等式中的L2的變化曲線。為了更加明顯地比較3個L2的差別，圖5(D)為計算出的3個L2的差值變化曲線。

?

　　如圖5(D)所示，勵磁涌流時3個L2差別很小，而在內部匝間短路時其差別較大，可以利用判據2可靠地區分勵磁涌流和輕微內部故障。

　　6 結論

　　該變壓器保護方案是利用變壓器正常運行時的模型來構成動作方程，由于只有在變壓器內部發生故障時，本方程才不再成立，所以此方案不受勵磁涌流的影響，并且在內部故障時有較高的靈敏度。該原理實現簡單，避開了變壓器難以取得的內部參數。仿真試驗結果表明該方案能夠可靠、迅速地切除變壓器內部故障。