隨著我國加入WTO 并逐步與國際市場接軌，高性能電池的使用量正大幅度增加，作為扣式電池一種的鋰錳電池正是其中之一。本文旨在依據公理化設計理論進行生產系統的方案設計，利用先進的設計理念解決自動組裝生產線系統這一難題。

　　公理化設計理論將機電產品作為整體的系統來看待，通過對功能需求域及設計參數域進行的解耦與耦合分析，得出最合理的優化設計方案。

　　1 公理化設計理論簡述

　　公理化設計理論(Axiomatic Design Theory)是由美國麻省理工大學的Nam P.Suh 提出的。這種理論將信息量引入設計過程，是一種可量化的設計原理。它創造性地將設計過程描述成一種映射過程，即通過選擇適當的設計參數，在功能需求域(FR)和設計參數域(DP)之間建立映射，映射過程遵循獨立性公理和信息公理，如圖1 所示。

?

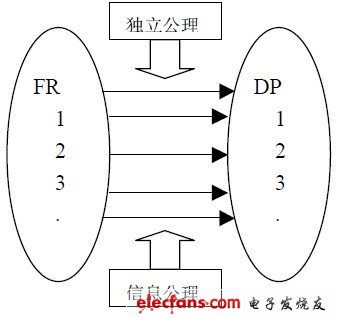
　　圖1 原理示意圖

　　獨立性公理即要求設計參數能保證功能需求的獨立性，也就是說當調整某一個DP 來滿足與之對應的FR 時，不影響其他的FR功能參數，在設計方案中每個單元都能獨立地完成與之相關的所有功能域需求，單元之間只交換相關數據信息，而保持一定程度的相互獨立性能，這樣同時也滿足信息公理的要求;信息公理即在滿足功能需求的前提下，使設計方案中的信息量最小，這樣能極大地簡化建立數學模型的過程，同時減少設計過程中不必要因素的影響，降低控制難度和準確測量難度，方案更容易實現。

　　在公理化設計理論中，從功能需求域到設計參數域的映射關系被描述成向量矩陣形式，以便于量化計算。因此兩者關系可表示為

　　{FR}=[A]{DP} (1-1)

　　其中{FR}為功能需求域向量表示，{DP}為設計參數域向量表示，[A]稱為設計矩陣(Design Matrix)。根據獨立性公理的要求，當功能需求向量個數與設計參數向量個數相等時，[A]呈現對角方陣，即

　　A={Aij=0 i≠j;Aij=1 i=j}

　　此時，[A]為非耦合矩陣，這樣的設計為非耦合設計。這是滿足獨立性公理的最優設計方案，同時也是信息量最少的設計方案。在不能完全滿足獨立性公理的時候，則需要采用解耦的方法，將[A]轉變為下三角矩陣，這樣可以通過順序調整各設計參數來滿足功能需求，調整時不影響已滿足的功能需求，其信息量在特定范圍內為最小，這種設計稱為解耦設計。信息量則以功能需求成功概率的倒數的對數來定義，即對于一個在基本取值全程上精度分布為均勻的功能需求來說，其信息量為

　　I=log(L/2ΔL) (1-2)

　　其中，在L 上得到L 精確值的概率

　　p=2ΔL/L (1-3)

　　在這里，L 為某一FR 的基本值，±ΔL 為其精度范圍。為了應用電子計算機計算信息量，習慣于用二進制位數度量信息量，多取底數為2 的對數。這樣，設計對象的總信息量即為

　　IT=ΣIj (1-4)

　　根據信息公理的要求，設計方案應盡力使IT 最小，以較小的復雜性滿足功能需求。

　　從一個完整的機電系統來看，依據公理化設計理論，設計過程可以量化為對功能需求域和設計參數域的信息量計算。[3]通過對FR 和DP 的系統性分析，得到非耦合性設計。對于不能得到非耦合設計的，采用解耦的辦法得到優化的解耦設計。同時分別計算功能需求信息量和設計參數信息量，其中設計參數又分為結構參數和時域控制參數，將計算的信息量進行比較。在保證設計域信息量滿足功能域信息量的要求情況下，依據兩條設計公理，尋求獨立性最好的最小信息量設計方案，即最優的設計方案。

　　相等時，[A]呈現對角方陣，即

　　A={Aij=0 i≠j;Aij=1 i=j}

　　此時，[A]為非耦合矩陣，這樣的設計為非耦合設計。這是滿足獨立性公理的最優設計方案，同時也是信息量最少的設計方案。在不能完全滿足獨立性公理的時候，則需要采用解耦的方法，將[A]轉變為下三角矩陣，這樣可以通過順序調整各設計參數來滿足功能需求，調整時不影響已滿足的功能需求，其信息量在特定范圍內為最小，這種設計稱為解耦設計。信息量則以功能需求成功概率的倒數的對數來定義，即對于一個在基本取值全程上精度分布為均勻的功能需求來說，其信息量為

　　I=log(L/2ΔL) (1-2)

　　其中，在L 上得到L 精確值的概率

　　p=2ΔL/L (1-3)

　　在這里，L 為某一FR 的基本值，±ΔL 為其精度范圍。為了應用電子計算機計算信息量，習慣于用二進制位數度量信息量，多取底數為2 的對數。這樣，設計對象的總信息量即為

　　IT=ΣIj (1-4)

　　根據信息公理的要求，設計方案應盡力使IT 最小，以較小的復雜性滿足功能需求。

　　從一個完整的機電系統來看，依據公理化設計理論，設計過程可以量化為對功能需求域和設計參數域的信息量計算。[3]通過對FR 和DP 的系統性分析，得到非耦合性設計。對于不能得到非耦合設計的，采用解耦的辦法得到優化的解耦設計。同時分別計算功能需求信息量和設計參數信息量，其中設計參數又分為結構參數和時域控制參數，將計算的信息量進行比較。在保證設計域信息量滿足功能域信息量的要求情況下，依據兩條設計公理，尋求獨立性最好的最小信息量設計方案，即最優的設計方案。

　　2 鋰錳扣式電池組裝工藝

　　以CR2032 組裝工藝為例，需要在帶有集流網、負極片的負極殼體內依次加入隔膜和飽浸電解液的正極片，并在保證電解液完全滲透的前提下，加蓋正極殼體并封口。經過廣泛的市場調研，根據相關廠家要求，確定以下成熟工藝。

　　2.1 傳送符合要求的負極殼體進入生產線系統

　　負極片是直徑為16mm，厚度約為0.4mm 的鋰片。要求把集流網點焊在負極殼底部，并把負極片壓在集流網上，使其接觸良好。這種負極殼體通過傳送機構進入生產線，作為整個系統的基本物流。

　　2.2 剪切隔膜紙，并壓入負極殼體

　　一般采用聚丙烯隔膜，依靠剪切機構裁成直徑約為18.8mm 的圓片，然后由壓入機構入殼。

　　2.3 加入以MnO2 為主要材料的正極片，并保證電解液浸透容量

　　正極片是直徑約為16mm，厚度約為2mm 的復合材料圓片，其主要材料為MnO2。正極片必須充分浸透電解液以保證放電時間及電池容量的性能參數，并通過控制補液時序避免電液揮發的影響。

　　2.4 覆蓋正極殼體，調整規正后封口并退料

　　傳送正極鋼殼到上料位置，覆蓋已完成滲透的負極殼體，并在規整機構作用下進入封口模具，完成封口工作，最后退出成品。

　　3 方案論證過程流程

　　依據以上組裝工藝要求對功能需求域進行分析，然后提出相應的設計參數。通過解耦和耦合計算，形成符合獨立性公理的設計方案，并對方案進行量化分析，根據信息公理評判方案的優劣與好壞。值得注意的是，由于以組裝工藝為基本依據，無論FR 域還是DP 域，每個因素在實行范圍內所占的比例各不相同，因此在方案論證時應注意增加權重因素。

　　具體方案論證的實施流程由圖2 表示。

?

　　圖2 方案論證過程流程

　　4 生產系統功能需求分析

　　從整體機械電子產品系統的角度出發，由于組裝工藝要求比較紛雜，其功能需求應從基本工藝要求和外界環境交流兩個方面分析入手。基本工藝要求部分保證了設計機構能完成組裝任務的主功能參數;外部環境交流部分從物質、信息、能量、人機等四個方面提出與系統功能相關的輔助需求參數，兩部分結合起來共同形成系統功能需求。這些參數既是系統設計參數分析的根本依據，也是功能需求域信息量計算的基本數據。

　　下面的表1 列出了功能需求分析參數結果，針對各個參數在生產系統中需求程度的不同，結果中包含權重因素。權重集的確定有很多方法，例如1 至9 比率標度法、相關專業專家打分法等等。為了了解實用行業的需求，在對國內幾個電池生產廠家和設備加工領域進行調研后，采用專家打分法得出如下的權重值，其中基本工藝要求屬于設計參數必須予以保證的功能結果，故占據60%的信息量比例。

　　表1

?

　　根據以上的功能需求分析結果，由式(1-2)(1-3)(1-4)可得計算功能需求域總信息量如下：

?

　　5 生產系統設計參數分析

　　針對功能需求分析的要求，應提出相應的設計參數。在基本工藝要求中，FR1、FR2、FR5、 FR6 均屬于固定要求，可以通過結構參數來實現;FR3、FR4 則需要結構參數和時域參數共同實現，因其加工檢測量都隨著時間變化而發生改變。同樣道理，對于其他各方面的功能需求也需要相應的結構參數或時域參數來滿足，這些參數并不一定是最終的設計參數，但它們是獨立性解耦和耦合的基本信息。設計參數分析如表2。

　　表2

?

　　6 解耦及耦合的設計過程

　　依據以上功能需求域的具體要求和設計參數域的基本實現參數，下一步工作的目的是通過解耦的方法來發現設計過程中的工程沖突和冗余單元，然后依靠耦合的辦法解決工程沖突和去除冗余單元，最終實現各工作單元的相對獨立(獨立性公理)和設計域信息量最小(信息公理)的系統設計要求。通常認為機械電子產品具有這樣從大到小的三級結構：機械電子系統(Mechanical Electronics SySTem-MES)、機械電子組元(MechaNICal ElectrONICS Component-MEC)、機械電子單元(Mechanical ElectronicsElement-MEE)。解耦和耦合的目標就是使機械電子產品形成這樣的規律性獨立結構體系。在這里，根系統(基本功能需求和設計參數層次)分析的目的就是能夠形成逐個獨立的機械電子組元，形成基本的設計參數類別;子系統(機械電子組元內部層次)分析則是以機械電子組元為分析對象，從中構建獨立的最小單位----機械電子單元，使信息量的計算從最底層開始，結果更為精確。

　　6.1 根系統解耦耦合分析

　　解耦和耦合的方法有很多種，這里介紹一種較直觀的方法，即矩陣化簡法。

?

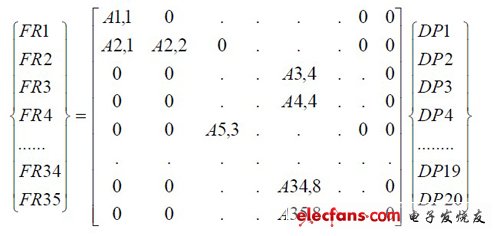
　　從上式可以看出，依據表2 列出的設計矩陣A 應是一個35 行20 列的矩陣，其中Aij 即設計矩陣的相關元素，代表了設計域參數域功能需求的內在聯系，很明顯尚不滿足公理設計原則的對角陣要求。需要對照表1 和表2 的注釋，對上式的左右兩邊做行列變換，逐步變設計陣為對角矩陣或者下三角矩陣。

　　值得注意的是，在這里的行列變換不是純粹數學意義上的初等變換，而是結合實際工程設計要求的的設計思想的轉變以矩陣行列變換的形式來表現，因此并不完全拘泥于固有的數學運算法則，而必須滿足工程設計中的基本原則和公理。這種矩陣化簡法能夠直觀的表現功能域和設計域的內在聯系，在解耦和耦合的步驟上也簡單明了，能夠解決設計中的工程沖突，并能有效去除冗余單元，不失為一種很好的實用方法。

　　經過行列變換，形成下面的下三角矩陣式：

?

　　式中各項意義如表3 所示。

　　表3

?

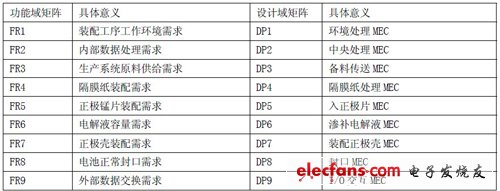
　　設計域矩陣中的各個機械電子組元(MEC)之間存在著最小的相關性，下一級設計參數的改變不會影響上一級參數的設計結果，而只影響包含其參數內容的再下級設計工作。完成根系統的解耦耦合分析后，還需要對各MEC 進行面向對象式的子系統分析，方法則采用子系統的公理化設計原理及方法。通過分別對子系統功能域和設計域進行具體層次的分析，最終得出各個基本滿足相對獨立性的基層最小系統——機械電子單元(MEE)。在機械電子單元中，各設計參數已具體量化，再依據信息公理及式(1-2)，精確計算方案設計的信息含量，形成對方案的完整優化設計。

　　6.2 子系統解耦耦合分析

　　對于子系統的分析集中在以下3 個方案上，通過對各設計子域和功能子域的分析得出各個方案的設計總信息量，如表4 所示。

　　表4

?

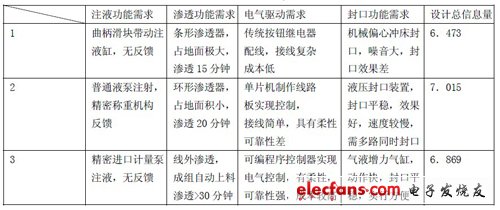
　　這三種方案除了以上主要區別之外，還存在諸如干燥功能需求、人機交互需求等次要區別，限于篇幅，不再贅述。下面給出第3 方案的子系統分析結果和單元信息量計算。其中單元信息量值根據各MEE的具體設計參量由式(1-2)計算得出。

　　表5

?

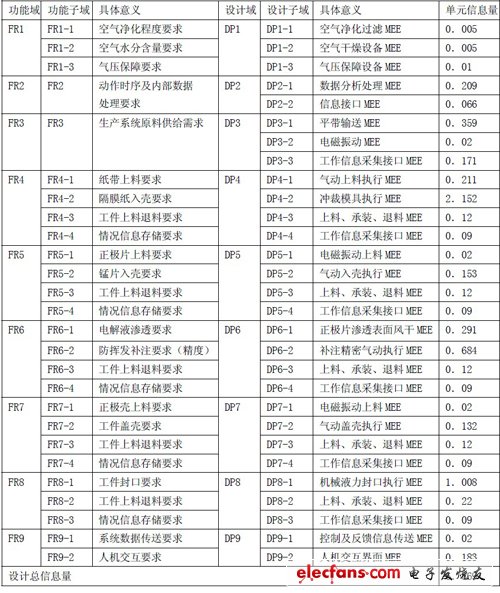
　　在第3 方案的解耦耦合分析中，去除了各層次的冗余單元，包括有關的結構參數和時域參數，用更加簡潔的功能原理方案加以解決，例如將包含注液監測機構、行進稱重機構及條形或環形行進機構在內的滲透單元改用單獨滲透和精密計量補注的設計單元來代替等等，不僅去除了冗余限制，降低加工制造成本，而且從根本上減小了動作控制及信號采集的難度，最優限度地利用了有用信息。

　　7 結論

　　從設計總信息量上分析，方案3 符合信息公理的要求，與功能需求域的總信息量相比較，設計參數域總信息量略高，在滿足功能需求的同時，又遵循了信息公理的要求。各機械電子單元也符合獨立性公理的要求，故應為最優方案。