0 引言

　　傳統單相升壓APFC電路已經被廣泛應用到功率因數校正電路中，但是該方案需要獨立的不可控整流橋，置后的升壓電感需要解決抗直流偏磁問題，而且升壓電感的位置很不利于整個功率電路的集成。這些引起了人們對傳統單相升壓APFC電路的重新思考，設想在利用其成熟控制思想與現成控制電路的前提下，使整個功率電路便于功率集成。近年來在這方面已經取得了很大進步，有多種電路拓撲被提出，其中雙向開關前置的單相升壓APFC變換器電路憑借其特有的性能引起了人們的關注。

　　1 雙向開關前置的單相升壓APFC變換器電路結構

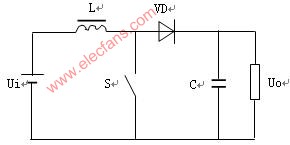
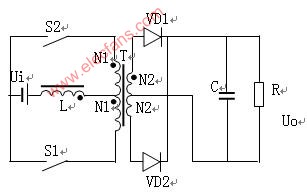
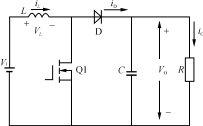
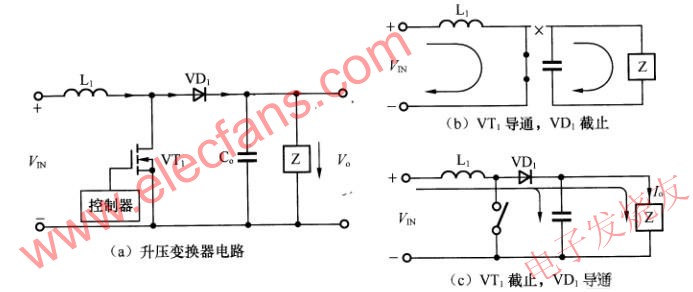
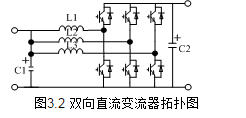
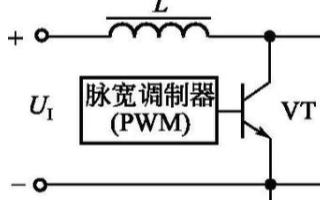
　　雙向開關前置的單相升壓APFC變換器的電路如圖1所示。輸入部分有交流電壓源VS和濾波電容C1組成。雙向開關S1和電感L完成功率因數校正功能，其中雙向開關S1由D5、D6、D7、D8和V1組成。整流部分由D1、D2、D3、D4構成，C2起儲能和輸出濾波的作用，R為負載。

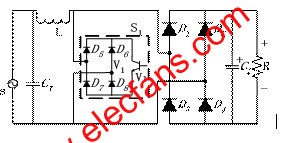
　　圖1 雙向開關前置的單相升壓APFC變換器主電路

　　2　雙向開關前置的單相升壓APFC變換器電路工作狀態分析

　　下文將對雙向開關前置的單相升壓APFC變換器電路動作過程進行分析。在連續導通模式下，對應開關管的一個高頻周期，流過電感L的電流iL，加在開關管V1兩端的電壓Vds和輸出電流i0的波形如圖2所示。對應各段時間的等效電路如圖3所示。其中工作狀態1和工作狀態2是工頻正半周時的情況，工作狀態3和工作狀態4是工頻負半周時的情況，后兩個狀態只是前兩個狀態在負半周的重復。為了分析方便，各二極管和開關管的導通壓降看作零，等效電路中的D1、D2、D3、D4、D5、D6、D7、D8僅表示電流流過的通路，C2看作足夠大，保證輸出電壓恒定，C2很小可以忽略不計。

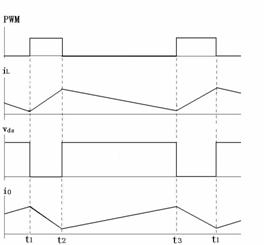
　　(a)正半周一個周期的波形

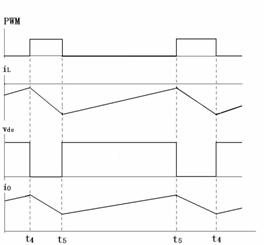
　　(b)負半周一個周期波形

　　圖2 變換器電路開關動作時iL、Vds、i0的波形

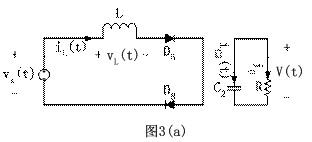
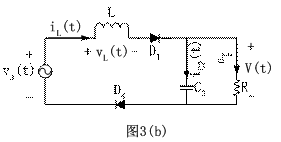
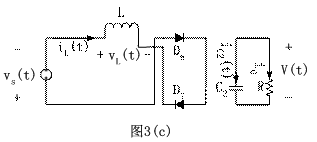
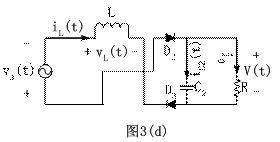
　　圖 3 各種工作狀態時的等效電路

　　2.1當VS處于正半周時的工作狀態

　　工作狀態1(t1

　　工作狀態2(t2

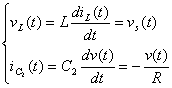
　　(1)

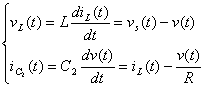
　　(2)

　　2.2當VS處于負半周時的工作狀態

　　工作狀態3(t4

　　工作狀態4(t5

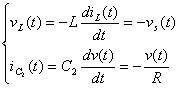
　　(3)

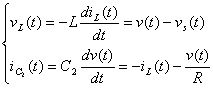
　　(4)

　　3 雙向開關前置的單相升壓APFC變換器電路小信號建模

　　對于雙向開關前置的單相升壓APFC變換器電路而言，在CCM工作模式下，由于后兩個狀態只是前兩個狀態在負半周的重復，下面以正半周期兩個狀態為例進行分析。為了求解變換器的靜態工作點，需要消除變換器中各變量的高頻開關分量，通常采用求平均值的方法。在滿足低頻假設和小紋波假設的情況下，定義變量電感電流i(t)、電容電壓v(t)和輸入電壓vs(t)在開關周期Ts內的平均值

　　、

　　和

　　為：

　　(5)

　　(6)

　　(7)

　　為了簡化分析，將有源開關元件與二極管都視為理想元件。則在CCM模式下變換器的每個開關周期都有兩種工作狀態。可以分別列出電感電壓和電容電流的微分方程式(1)、(2)、(3)、 (4)，然后結合(5)、(6)、(7)式就可以分別得到電感電壓和電容電流在一個開關周期內的平均值，進一步可以導出變換器的一組非線性平均變量狀態方程(8)、(9)。

　　(8)

　　(9)

　　(8)、(9)是一組非線性狀態方程，各平均變量和控制變量d(t)中同時包含著直流分量和低頻小信號分量。在電路滿足小信號假設的情況下，可以分離出電感和電容的交流小信號狀態方程為(10)、(11)。

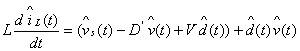
　　(10)

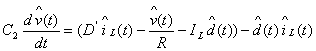
　　(11)

　　變換器的實際工作狀態是工作在靜態工作點附近并且按線性規律變化。但是(10)、(11)兩式組成的交流小信號狀態方程仍為非線性狀態方程，因此還需要對非線性方程線性化。由于(10)、(11) 兩式中除了

　　、

　　外都為線性項，而且這兩乘積項遠小于其它項，若將它們略去，不會給分析引入太大誤差，則線性化后的交流小信號狀態方程為(12)、(13)。

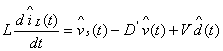
　　(12)

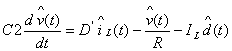
　　(13)

　　根據方程 (12)、(13)可以建立更為直觀的交流小信號等效電路模型，為分析變換器的小信號特性提供方便，如圖5所示：

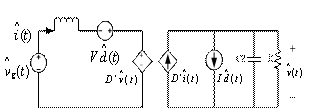
　　圖4 雙向開關前置的單相升壓APFC變換器在CCD模式下的交流小信號等效模型

　　4 雙向開關前置的單相升壓APFC變換器仿真分析

　　下面利用MATLAB7.1中的Simulink6.0仿真軟件對變換器電路進行仿真，假定參數設置如下：Vs=220V，初級電感L=1×10-3H，初級濾波電容C1=3.3μF，輸出儲能電容C2=200~5000μF，開關管的工作頻率為fS=50KHz，負載R=20~140Ω。下面分別討論儲能電容C2和負載R的變化對功率因數(PF)和輸出紋波電壓(Vpp)的影響。

　　4.1參數變化對電路的功率因數(PF)的影響

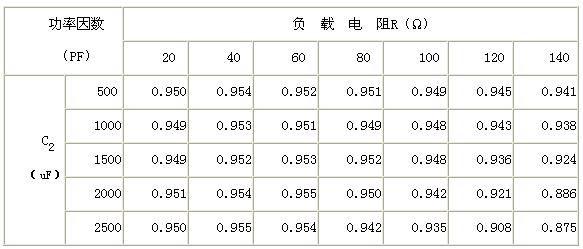
　　參數變化會對電路的功率因數(PF)產生影響，以橋臂并聯電容C2和負載R為變量，仿真求得電路的PF值，結果如表 1所示：

　　表 1 功率因數隨輸出側并聯電容值及負載變化的仿真結果

　　點擊看原圖

　　電容C2分別取500uF、1000uF、1500uF、2000uF、2500uF時，負載在20Ω～140Ω范圍內對應分別取7組數據，利用MATLAB軟件對各PF值進行三次多項式插值，插值后的變化曲線如圖5所示。

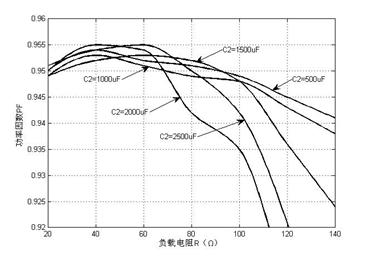
　　圖5 功率因數隨輸出側并聯電容值及負載變化的PF插值曲線

　　從圖5可以看出，針對某一取值的電容，負載的變化對功率因數有很大影響，當40Ω≤R≤60Ω時，功率因數取得較大值。

　　4.2參數變化對電路的輸出紋波電壓(Vpp)的影響

　　參數的變化同樣會影響電路的輸出紋波電壓(Vpp)，以橋臂并聯電容C2和負載R為變量，仿真求得電路的輸出紋波電壓值如表2所示。

　　表2 輸出紋波電壓隨輸出側并聯電容值及負載變化的仿真結果

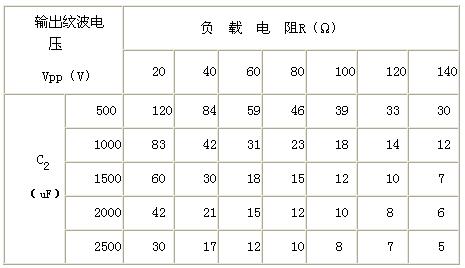
　　電容C2分別取500uF、1000uF、1500uF、2000uF、2500uF時，負載在20Ω～140Ω范圍內對應分別取7組數據，利用MATLAB軟件對輸出紋波電壓(Vpp)進行三次多項式插值，插值后的變化曲線如圖6所示。

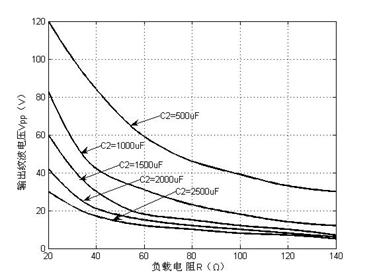
　　圖6 功率因數隨輸出側并聯電容值及負載變化的PF插值曲線

　　從圖6可以看出，紋波電壓值隨負載電阻的增大而減小，負載電阻越大，紋波越小，輸出電壓越平滑。在實際應用中要同時兼顧設計要求和成本，一般來講輸出電壓紋波(Vpp)在滿載的情況下不大于20V就可以滿足要求，這時候要盡可能考慮到成本，電容體積等因素，所以C2取1500uF左右即可。

　　綜上所述，如果要求輸出紋波電壓VPP在20V以內，電容又不太大，優先考慮功率因數的情況下，結合體積、經濟性等因素，則該電路的最佳參數選擇為：C2取值在1500uF左右，R取40Ω≤R≤60Ω。

　　4.3最佳參數情況的實例仿真

　　下面針對最佳參數情況進行仿真，參數設置如下： Vs="220V"，初級電感L=1×10-3H，初級濾波電容C1=3.3μF，輸出儲能電容C2=1500μF，開關管的工作頻率為fS=50KHz，負載R=50Ω。

　　仿真結果如下：

　　系統進入穩態后，輸入電壓電流波形如圖7所示。可以看出變換器輸入電流很好的跟蹤了輸入電壓的波形。為了便于比較，圖中交流電壓Vs幅值是原來的1/20，每一格代表20伏特，電流的單位是安培。

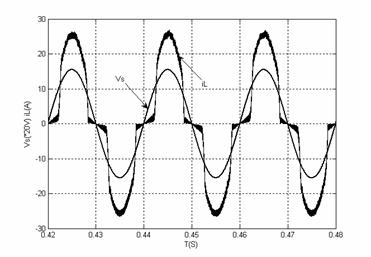
　　圖7 輸入電壓電流波形

　　功率因數的曲線如圖8所示，從圖中可以看出在0.15秒以前電路處于非穩定狀態，功率因數有較大跳變，在0.15秒以后電路進入穩定狀態，功率因數可以達到0.95以上。

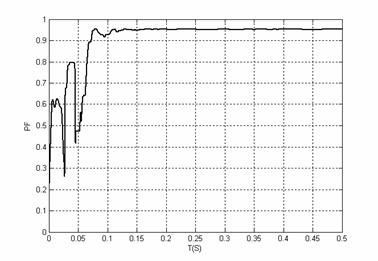
　　圖8 功率因數的曲線

　　輸出電壓波形如圖9所示，從圖中可以看出輸出平均電壓為400V左右，通過放大后的可以看出紋波電壓的峰峰值為15V，該電路電容電壓被很好的限制在一定的范圍內，儲能電容的耐壓大大減少，保證了電路的輸出特性。

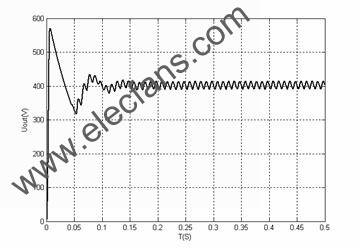
　　圖9 輸出電壓波形

　　5 結論

　　雙向開關前置的單相升壓APFC變換器電路把雙向開關放置在整流橋前端，較好的解決了傳統單相升壓APFC變換器電路置后的升壓電感直流偏磁問題，也便于電路的集成。通過優化電路參數配置可以實現很高的功率因數，而且輸出電壓穩定，輸出紋波電壓低，能夠獲得很好的輸出特性。本文通過仿真找到了比較好的參數配置范圍，對實際應用具有重要的指導意義。