常見的幾種二極管整流電路解析:
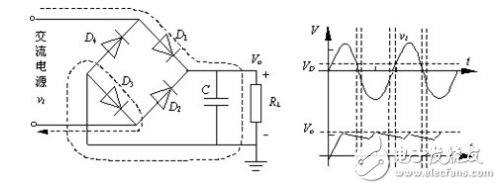
二極管半波整流電路實際上利用了二極管的單向導電特性。
當輸入電壓處于交流電壓的正半周時,二極管導通,輸出電壓vo=vi-vd。當輸入電壓處于交流電壓的負半周時,二極管截止,輸出電壓vo=0。半波整流電路輸入和輸出電壓的波形如圖所示。
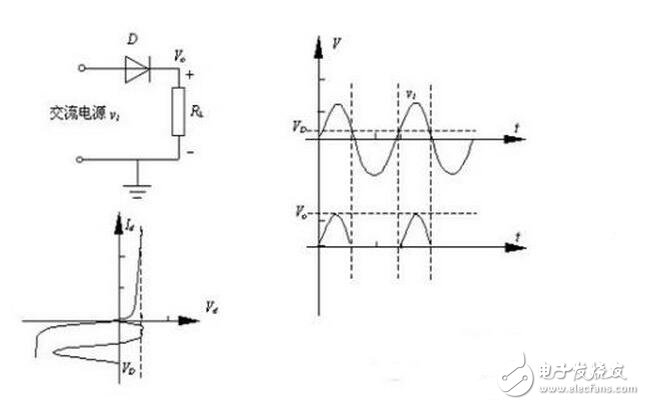
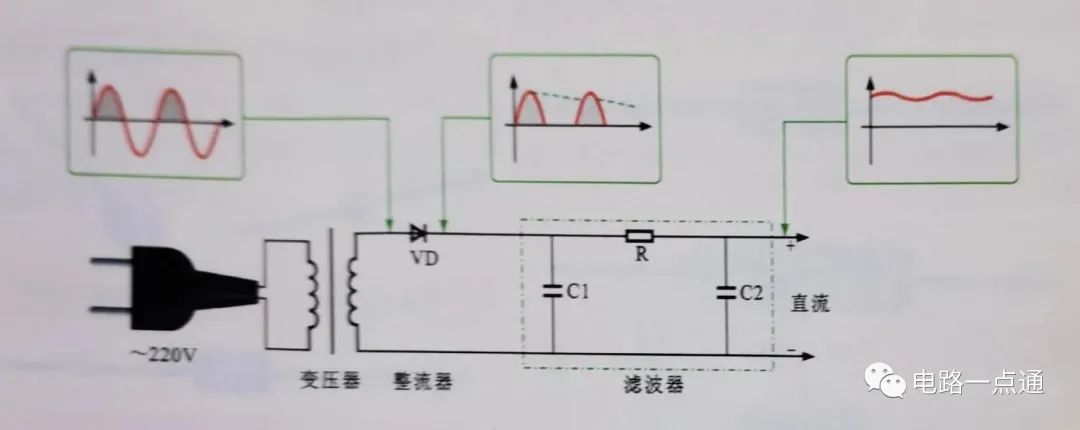
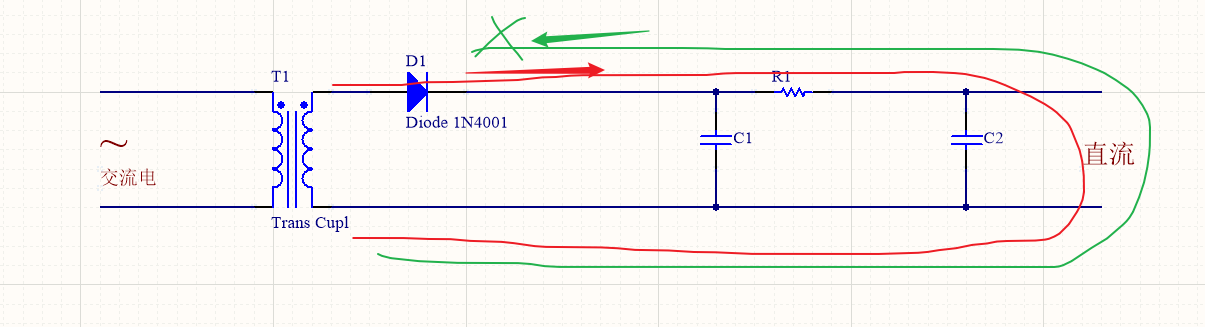
對于使用直流電源的電動機等功率型的電氣設備,半波整流輸出的脈動電壓就足夠了。但對于電子電路,這種電壓則不能直接作為半導體器件的電源,還必須經過平滑(濾波)處理。平滑處理電路實際上就是在半波整流的輸出端接一個電容,在交流電壓正半周時,交流電源在通過二極管向負載提供電源的同時對電容充電,在交流電壓負半周時,電容通過負載電阻放電。
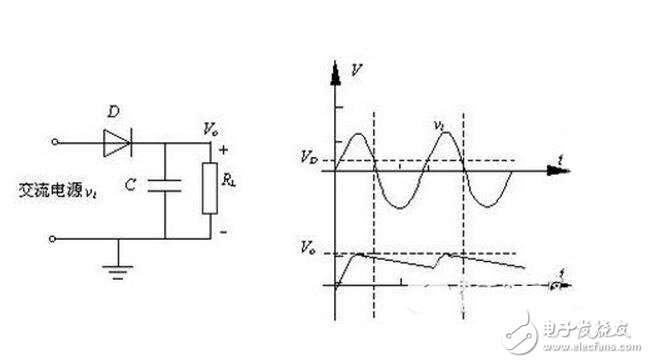
通過上述分析可以得到半波整流電路的基本特點如下:
(1)半波整流輸出的是一個直流脈動電壓。
(2)半波整流電路的交流利用率為50%。
(3)電容輸出半波整流電路中,二極管承擔最大反向電壓為2倍交流峰值電壓(電容輸出時電壓疊加)。
(3)實際電路中,半波整流電路二極管和電容的選擇必須滿足負載對電流的要求。
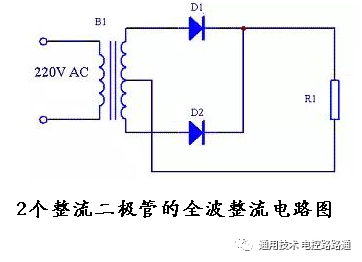
全波整流
當輸入電壓處于交流電壓的正半周時,二極管D1導通,輸出電壓Vo=vi-VD1。當輸入電壓處于交流電壓的負半周時,二極管D2導通,輸出電壓Vo=vi-VD2。
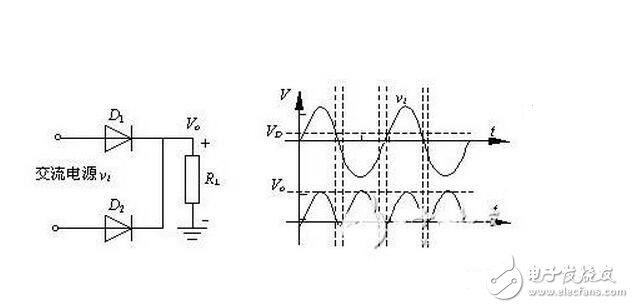
由上述分析可知,二極管全波整流電路輸出的仍然是一個方向不變的脈動電壓,但脈動頻率是半波整流的一倍。
晶體二極管組成的各種整流電路。
一、半波整流電路
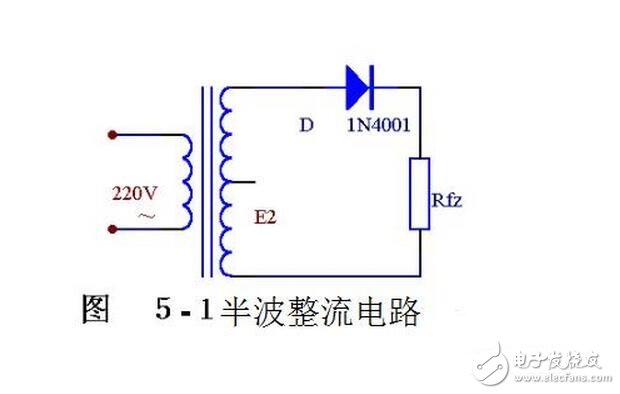
下面從圖5-2的波形圖上看著二極管是怎樣整流的。 圖5-1、是一種最簡單的整流電路。它由電源變壓器B 、整流二極管D 和負載電阻Rfz ,組成。變壓器把市電電壓(多為220伏)變換為所需要的交變電壓e2,D 再把交流電變換為脈動直流電。
變壓器砍級電壓e2,是一個方向和大小都隨時間變化的正弦波電壓,它的波形如圖5-2(a)所示。在0~K時間內,e2為正半周即變壓器上端為正下端為負。此時二極管承受正向電壓面導通,e2通過它加在負載電阻Rfz上,在π~2π 時間內,e2為負半周,變壓器次級下端為正,上端為負。這時D承受反向電壓,不導通,Rfz,上無電壓。在π~2π時間內,重復0~π 時間的過程,而在3π~4π時間內,又重復π~2π時間的過程…這樣反復下去,交流電的負半周就被“削”掉了,只有正半周通過Rfz,在Rfz上獲得了一個單一右向(上正下負)的電壓,如圖5-2(b)所示,達到了整流的目的,但是,負載電壓Usc。以及負載電流的大小還隨時間而變化,因此,通常稱它為脈動直流。
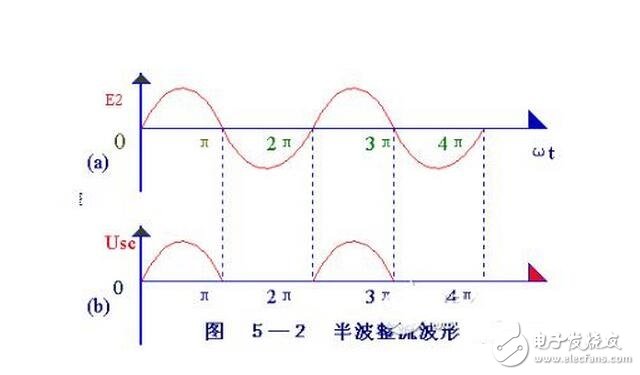
這種除去半周、圖下半周的整流方法,叫半波整流。不難看出,半波整說是以“犧牲”一半交流為代價而換取整流效果的,電流利用率很低(計算表明,整流得出的半波電壓在整個周期內的平均值,即負載上的直流電壓Usc =0.45e2 )因此常用在高電壓、小電流的場合,而在一般無線電裝置中很少采用。
二極管整流電路電路賞析
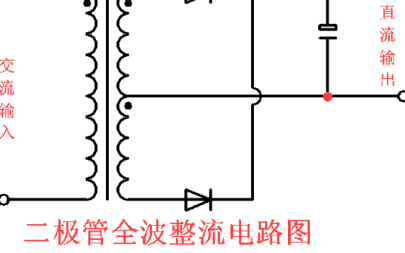
全波整流電路
如果把整流電路的結構作一些調整,可以得到一種能充分利用電能的全波整流電路。圖5-3 是全波整流電路的電原理圖。

全波整流電路,可以看作是由兩個半波整流電路組合成的。變壓器次級線圈中間需要引出一個抽頭,把次組線圈分成兩個對稱的繞組,從而引出大小相等但極性相反的兩個電壓e2a 、e2b ,構成e2a 、D1、Rfz與e2b 、D2、Rfz ,兩個通電回路。
全波整流電路的工作原理,可用圖5-4 所示的波形圖說明。在0~π間內,e2a 對Dl為正向電壓,D1導通,在Rfz 上得到上正下負的電壓;e2b 對D2為反向電壓,D2 不導通(見圖5-4(b)。在π-2π時間內,e2b 對D2為正向電壓,D2導通,在Rfz 上得到的仍然是上正下負的電壓;e2a 對D1為反向電壓,D1 不導通(見圖5-4(C)。
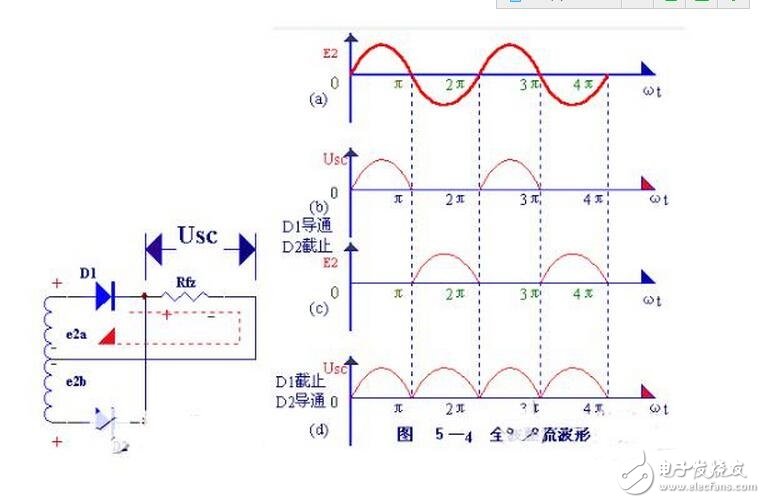
如此反復,由于兩個整流元件D1、D2輪流導電,結果負載電阻Rfz 上在正、負兩個半周作用期間,都有同一方向的電流通過,如圖5-4(b)所示的那樣,因此稱為全波整流,全波整流不僅利用了正半周,而且還巧妙地利用了負半周,從而大大地提高了整流效率(Usc=0.9e2,比半波整流時大一倍)。
圖5-3所示的全波整濾電路,需要變壓器有一個使兩端對稱的次級中心抽頭,這給制作上帶來很多的麻煩。另外,這種電路中,每只整流二極管承受的最大反向電壓,是變壓器次級電壓最大值的兩倍,因此需用能承受較高電壓的二極管。
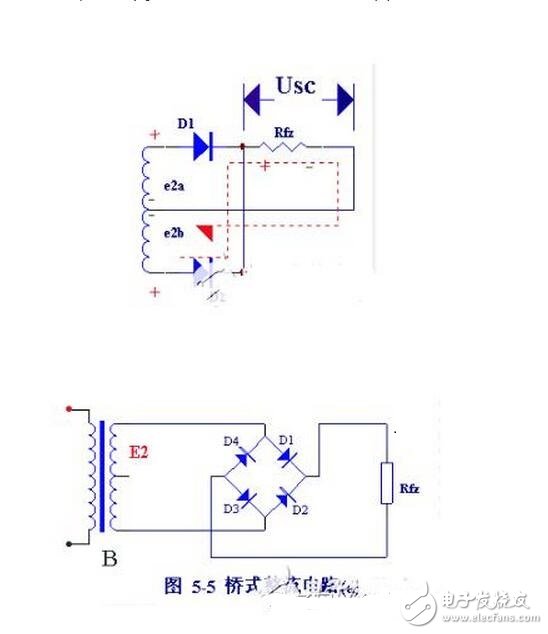
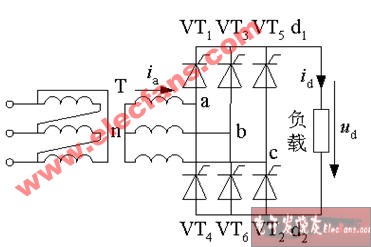
圖5-5(a )為橋式整流電路圖,(b)圖為其簡化畫法。
橋式整流電路
橋式整流電路是使用最多的一種整流電路。這種電路,只要增加兩只二極管口連接成“橋”式結構,便具有全波整流電路的優點,而同時在一定程度上克服了它的缺點。
橋式整流電路的工作原理如下:e2為正半周時,對D1、D3和方向電壓,Dl,D3導通;對D2、D4加反向電壓,D2、D4截止。電路中構成e2、Dl、Rfz 、D3通電回路,在Rfz ,上形成上正下負的半波整洗電壓,e2為負半周時,對D2、D4加正向電壓,D2、D4導通;對D1、D3加反向電壓,D1、D3截止。電路中構成e2、D2Rfz 、D4通電回路,同樣在Rfz 上形成上正下負的另外半波的整流電壓。
上述工作狀態分別如圖5-6(A) (B)所示。
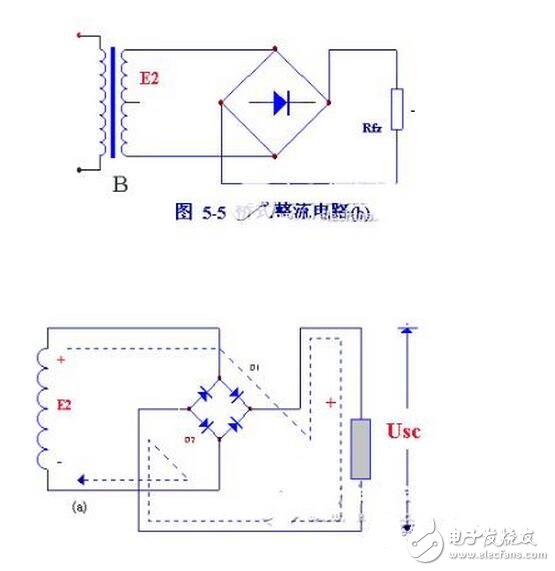
如此重復下去,結果在Rfz ,上便得到全波整流電壓。其波形圖和全波整流波形圖是一樣的。從圖5-6中還不難看出,橋式電路中每只二極管承受的反向電壓等于變壓器次級電壓的最大值,比全波整洗電路小一半!
整流元件的選擇和運用
需要特別指出的是,二極管作為整流元件,要根據不同的整流方式和負載大小加以選擇。。如選擇不當,則或者不能安全工作,甚至燒了管子;或者大材小用,造成浪費。表5-1 所列參數可供選擇二極管時參考。
“另外,在高電壓或大電流的情況下,如果手頭沒有承受高電壓或整定大電濾的整流元件,可以把二極管串聯或并聯起來使用。
圖5-7 示出了二極管并聯的情況:兩只二極管并聯、每只分擔電路總電流的一半口三只二極管并聯,每只分擔電路總電流的三分之一。總之,有幾只二極管并聯,”流經每只二極管的電流就等于總電流的幾分之一。但是,在實際并聯運用時“,由于各二極管特性不完全一致,不能均分所通過的電流,會使有的管子困負擔過重而燒毀。因此需在每只二極管上串聯一只阻值相同的小電阻器,使各并聯二極管流過的電流接近一致。這種均流電阻R一般選用零點幾歐至幾十歐的電阻器。電流越大,R應選得越小。
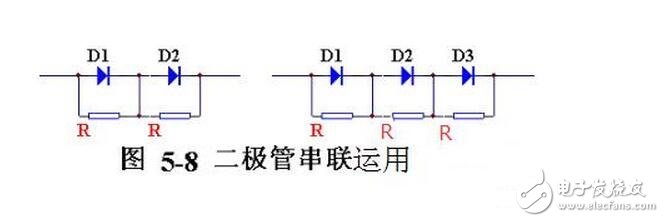
圖5-8示出了二極管串聯的情況。顯然在理想條件下,有幾只管子串聯,每只管子承受的反向電壓就應等于總電壓的幾分之一。但因為每只二極管的反向電阻不盡相同,會造成電壓分配不均:內阻大的二極管,有可能由于電壓過高而被擊穿,并由此引起連鎖反應,逐個把二極管擊穿。在二極管上并聯的電阻R,可以使電壓分配均勻。均壓電阻要取阻值比二極管反向電阻值小的電阻器,各個電阻器的阻值要相等。 向電阻值小的電阻器,各個電阻器的阻值要相等。
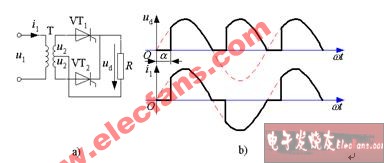
可控硅整流電路波形原理分析:
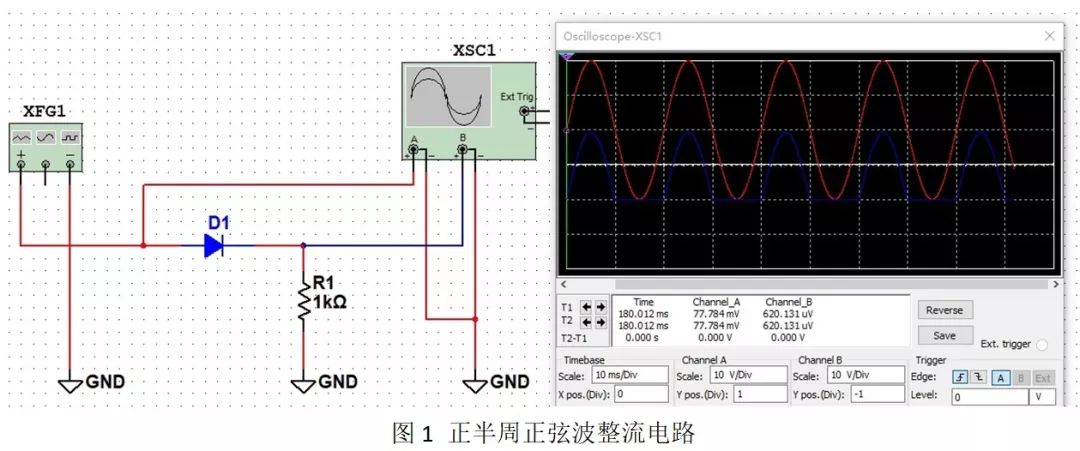
某一電壓(或電流)的有效值與其平均值之比,我們稱之為波形系數。在可控硅整流電路中波形系數是個值得注意的問題。為說明這個問題,我們先按圖1所示的可控硅半波整流電路做個實驗,各元件的型號和參數僅供參考。
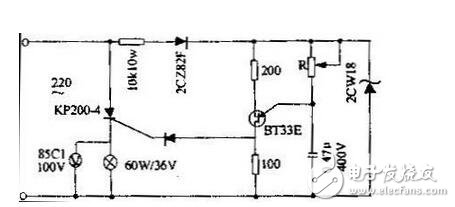
先將R值調至最大,接通電源,此時直流電壓表指示為零,燈泡不亮。然后慢慢減小R值,電壓表讀數逐漸增大,燈泡逐漸增亮。我們會發現當直流電壓表指示為10伏時,燈泡便達到正常亮度了,這就是說燈泡的功耗已達額定功率了,若再繼續增高電壓,燈泡就可能燒毀。為什么電壓表的讀數還遠沒有達到燈泡的額定電壓36伏,而燈泡的功耗卻已達到額定功率了呢?
燈光中流過的電流是單向脈動電流,燈泡兩端的電壓為單向脈動電壓,其波形如圖2中實線所示。直流電壓表的讀數是這種脈動電壓的平均值,而刁;是它的有效值。其有效值卻要比平均值大得多。
根據電工學知識,這種周期性的單向脈動電壓的有效值U。乃是瞬時值的平方在一個周期內平均值的算術平方根(均方根值),即

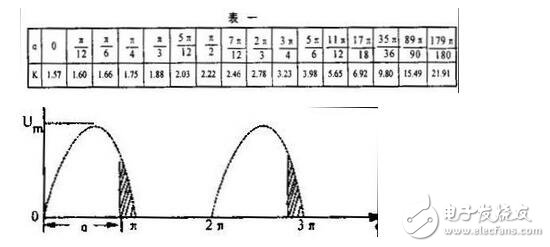
將不同的Q值代入式(3),就得到相應的K值,如表一所示。由表一可以看出,當可控硅的移相角由零變到n時,波形系數K值逐漸增大,而且增大的速度越來越快,當。接近,I時,K值將急聚增加(而U和Uo都急聚下降。)
現在再來看看實驗結果。據式(2)可算出,當直流電壓表指示10伏即U。=10伏時,CO$n=-0.7979,波形系數K~3.57, Uo~35.7伏。Uo己相當接近燈泡的額定電壓了,所以燈泡達到正常亮度。
根據同樣的道理可算出, 當G相同時,在電阻性負載的全波可控整流電路中,輸出脈動電壓(波形見圖3中的實線)系數的1//2倍。在上述計算中,均忽略了可控硅導通時的正向壓降。對其他形式的整流電路以及負載呈電感性時輸出電壓的波形系數,本文不再贅述。
由上面的分析可知,在用可控硅進一行整流時,直流電壓表(或電流表)上L的讀數是輸出電壓(或電流)的平均1K值,不能將讀數直接代入公式卜U2 L來計算負載上的功耗,這是因為式中U為負載R,上的電壓有效值,即U=Uo。
如欲減小波形系數,使輸出出電壓有效值接近于平均值,有三條措施可取:
(1) 盡量減小可控硅的移相角,如Q:o時,則K=I.57(單相半波): (2)當負載額定電壓比輸入交流電壓的有效值低得多時,先用變壓器降壓再進行整流; (3)盡量采用單向可控整流或三相可控整流電路。如忽視波形系數的影響,盡管電壓表的讀數還遠未達到負載的額定電壓,但仍有可能燒毀電器,以致造成不應有的損失。這是必須注意的。
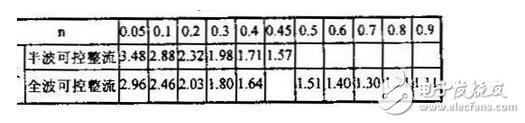
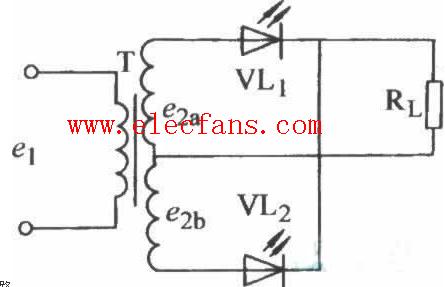
在實際應用中,為方便起見,我們可根據表二來估算不同的輸出直流電壓時的波形系數,從而估算出輸出電壓的有效值。表二中的n為直流電壓表的讀數U。與輸入交流電壓有效值U的比。即 23 (3),便可得到相應的波形系數K。例如在圖1所示的電路中,當直流電壓表指示為 50伏時,n=50/220~0.23,根據表二可估算出此時波形系數K在2.32和1.98之間。
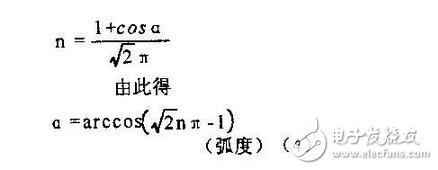
對于全波可控整流電路來說,
根據同樣的道理,可得出全波可控整流電路中,對應于不同n值(可控硅全導通時n取得最大值0.9)時的波形系數K
 電子發燒友App
電子發燒友App










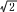










評論