快速傅里葉變換(FFT)算法實現的流水線結構FFT處理器在實時專用處理器中得到了廣泛應用.Bi和Jones提出一種固定1024點流水線FFT處理器結構，該結構在運算的每級只采用一個復數乘法器.基于此結構Hasan設計了一種能夠進行16，64，256和1024點FFT運算的可變點流水線FFT處理器，增強了處理器運用的靈活性.但該處理器結構所需的中間數據及旋轉因子存儲容量較大，各級的地址控制邏輯比較復雜，運算時間較長，不適于對速度和面積要求越來越高的應用場合.作者提出了一種實時可重配置的FFT處理器.該處理器采用小點數內部流水和大點數二維化處理結構，通過控制各處理模塊實現4,16,64，256和1 024點復數FFT運算，并給出了該結構與Hasan結構的性能比較.

　　1 可重配置FFT算法原理

　　N個樣本點的離散博里葉變換(DFT)表達式為

　　式(2)表明，計算組合數N=r1 r2點DFT等價于先求出r2組r1點的DFT，其結果乘以旋轉因子后，再計算r1組r2點的DFT.

　　基-4時間抽取FFT算法中，16點FFT運算可以分為兩級，第1級基本運算是4點序列的DFT.因此，如果只取16點FFT運算的第1級運算便可同時完成4點FFT運算.

　　2 可重配置FFT處理器的實現

　　2.1 系統設計

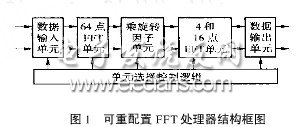
　　FFT處理器由數據輸入單元、固定64點FFT、流水處理單元、中間乘旋轉因子單元、4和16點FFT可變流水處理單元及數據輸出單元組成.如圖1所示.

　　在進行FFT運算時，單元選擇控制邏輯根據需要變換長度N激活相應的處理單元.

　　根據式(2)對1 024點輸入數據進行FFT運算，首先數據輸入單元要按照N=rlr2=64×16完成對輸入1 024點數據的分解，然后固定64點FFT流水處理單元完成16次64點運算.運算結果分別與1024個中間旋轉因子相乘，然后乘旋轉因子單元完成對這1 024個結果的整形，并使用4點和16點可變處理單元完成64次16點變換.數據輸出單元完成對結果進行最后整形并同時輸出1個塊浮點溢出檢測指數和1 024個數據結果.同理對于256點的FFT運算，數據輸入單元按照N=r1r2=64×4進行分解運算即可.

　　2.2 地址生成

　　可重配置FFT處理器包括輸入數據地址產生單元、64點數據旋轉因子地址產生單元、中間乘旋轉因子地址產生單元、中間數據存取地址產生單元、4，16點FFT數據及旋轉因子地址產生單元和輸出數據地址產生單元.每個單元都由計數器和地址變換器構成，每周期產生一組地址.由于采用的是Cooley-Tukey算法同址運算規則，倒序輸入正序輸出.因此針對不同長度的FFT運算，地址變換器只需要對計數器的輸出值進行不同的變形即可.

　　由于要實現的最大運算點數為1 024，同時采用流水乒乓存儲結構，因此輸入、中間、輸出單元的地址深度為2，則這3個地址產生器中的計數器為11位，最高位作為乒乓選擇控制位.產生的各個單元地址如圖2所示.中間數據地址產生單元只需要生成256點和1 024點數據地址即可.中間數據存地址即為輸入數據地址.輸出數據地址只需要產生4，16，256和1 024點數據地址.256個旋轉因子可從1 024個旋轉因子中抽取得到.產生的中間旋轉因子地址如圖3所示.