本文解釋了為什么ADC輸入阻抗隨頻率而變化,以及為什么這是個電路設計難題;然后比較了確定輸入阻抗的兩種方法:利用網絡分析儀測量法和利用數學分析方法計算法。本文還介紹了正確使用網絡分析儀的過程,并且提供了一個數學模型,其計算結果與實際測量結果非常接近。
“有緩沖”或“無緩沖”
考慮輸入阻抗的影響時,設計人員一般可以在兩類高速ADC之間選擇:有緩沖和無緩沖(即采用開關電容)。雖然有許多不同的轉換器拓撲結構可供選擇,但本文討論的應用僅涉及流水線架構。
常用的CMOS開關電容ADC無內部輸入緩沖器。因此,其功耗遠低于緩沖型ADC。外部前端直接連接到ADC的內部開關電容采樣保持(SHA)電路,這帶來兩個問題。
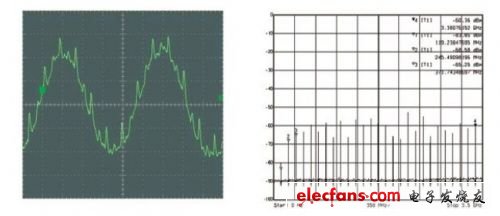
第一,當ADC在采樣與保持兩種模式之間切換時,其輸入阻抗會隨頻率和模式而變化。第二,來自內部采樣電容和網絡的電荷注入會將少量信號(與高頻成分混合,如圖1所示)反射回前端電路和輸入信號,這可能導致與轉換器模擬輸入端相連的元件(有源或無源)發生建立(settling)錯誤。
?
圖1:此圖反映了內部采樣電容的時域電荷注入(單端)與頻域電荷注入的對比關系。
通常,當頻率較低時(《100MHz),這類轉換器的輸入阻抗非常高(數千Ω左右);當頻率高于200MHz時,差分輸入阻抗跌落至大約200Ω。輸入阻抗的虛部(即容性部分)也是如此,低頻時的容抗相當高,高頻時逐漸變小到大約1-2pF。“匹配”這種輸入結構是個極具挑戰性的設計問題,特別是當頻率高于100MHz時。
輸入端采用差分結構很重要,尤其是對于頻域設計。差分前端設計能夠更好地對電荷注入進行共模抑制,并且有助于設計。
采用帶輸入緩沖的轉換器更便于設計。但不利的一面是這類轉換器的功耗更高,因為緩沖器必須設計得具有高線性和低噪聲特性。輸入阻抗通常規定為固定的差分R||C阻抗。它由一個晶體管級進行緩沖,該級以低阻抗驅動轉換過程,因此顯著減小了電荷注入尖峰和開關瞬變。
與開關電容型ADC不同,輸入終端在轉換過程的采樣和保持階段幾乎無變化。因此,相比于無緩沖型ADC,其驅動電路的設計容易得多。圖2為緩沖型和無緩沖型ADC的內部采樣保持電路的結構簡圖。

?
圖2: 所示是無緩沖(a)和有緩沖(b)高速流水線ADC采樣和保持電路的比較。
轉換器的選擇可能很難,但如今的大部分設計都力求更低功耗,因此設計人員往往采用無緩沖型轉換器。如果線性指標比功耗更重要,則通常選用緩沖型轉換器。應當注意,無論選擇何種轉換器,應用的頻率越高,則前端設計就越困難。單靠選擇緩沖型轉換器并不能解決所有問題。不過在某些情況下,它可能會降低設計復雜性。
轉換器輸入阻抗計算:測量方法
表面上,這似乎非常棘手,但其實有多種方法可以測量轉換器的阻抗。技巧在于利用網絡分析儀來完成大部分瑣碎工作,不過這種設備可能價格不菲。其優點是,當今的網絡分析儀能夠實現許多功能,像跡線計算和去嵌入等;對于阻抗轉換等任務,它可以直接給出答案,而不需要使用外部軟件。
測量轉換器的阻抗需要兩塊電路板、一臺網絡分析儀和一點“入侵”知識。第一塊板焊接有ADC/DUT(待測器件),還焊接了其它元件以提供偏置和時鐘(圖3a)。第二塊高速ADC評估板去除了前端電路,僅留連至轉換器模擬輸入引腳的走線(圖3b)。

?
圖3: ADC的阻抗測量需要一塊ADC評估板(a)且要將(a)中的前端去掉以用于測量(b)。
第二塊板除去了拆掉的前端電路的任何走線寄生效應。為此,必須使用與圖3b所示一模一樣但沒焊裝器件的電路裸板(圖4a)。然后切割該裸板,只剩下前端電路走線進入ADC的模擬輸入引腳的那部分(圖4b)。
?
圖4: 為去掉被剝離的前端電路的導線寄生效應,應使用圖3b所示的未焊件裸板(a)。該板的一個剪切版只允許前端電路導線連接到ADC的模擬輸入引腳(b)。
需要在轉換器的引腳處安裝一個連接器(通常會有足夠的銅來完成這一任務)。在此階段可發揮創造性以保證該連接器的牢固連接。通常,ADC的裸露焊盤(epad)可用于實現轉換器本身到地的連接。假設前端電路的兩條差分走線相等且對稱,那么只需要使用其中的一條走線。該板用于實現“通過”測量,最后將從焊有器件電路板的測量結果中減去前一測量結果。
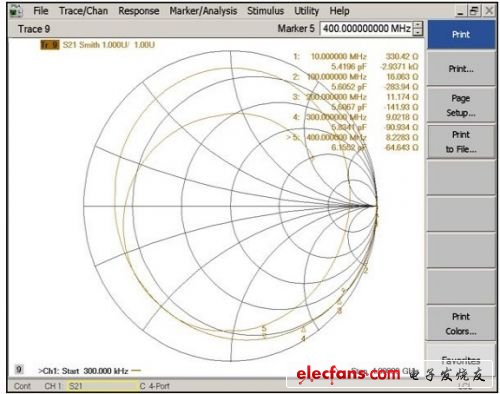
下一步是對剪切后的小裸板(圖4b所示的第二塊板)實施“通過”測量,以測量S21(圖5)。這個文件(應以touchstone格式或?.S2P文件形式保存)將成為去嵌入文件,用以從焊有器件的板中剔除所有走線寄生效應。
?
圖5: 圖4b所示剪切板的去掉前端電路后的導線阻抗。
然后只需以差分配置將焊件板(圖3b所示的第一塊板)連接到網絡分析儀。應為該板提供電源和時鐘,以確保能捕捉到測量過程中轉換器內部前端設計的任何寄生變化。
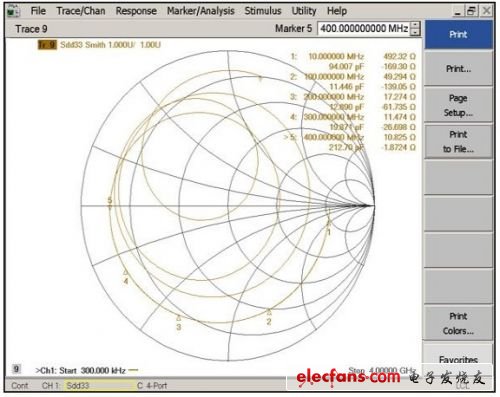
焊件板“上電”后,轉換器看起來像是在典型應用中。在此測量中,將先前在切割裸板的各端口(各模擬輸入走線)上測得的板寄生效應(圖6)去掉。最終將從當前ADC測量結果中減去板寄生效應,僅在圖中顯示封裝和內部前端阻抗(圖7)。
?
圖6: 這條曲線說明了沒去掉前端電路寄生效應的ADC阻抗。

?
圖7: 這條曲線說明了去掉前端電路寄生效應的ADC的阻抗。
轉換器輸入阻抗計算:數學方法
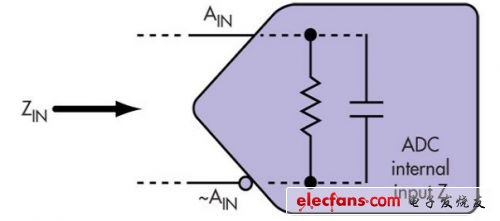
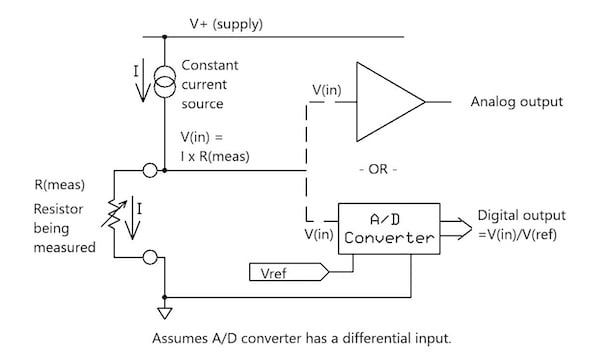
現在我們通過數學方法分析一下,看花在實驗室測量上的時間是否值得。可對任何轉換器的內部輸入阻抗實施建模(圖8)。該網絡是表述跟蹤模式下(即采樣時)輸入網絡交流性能的一個良好模型。
?
圖8: 跟蹤模式(實施采樣時)下,ADC內部輸入網絡的AC性能。
ADC internal input Z:ADC內部輸入阻抗
通常,任何數據手冊都會給出某種形式的靜態差分輸入阻抗、以及通過仿真獲得的R||C值。本文所述方式所用的模型非常簡單,目的是求出高度近似值并簡化數學計算。否則,如果等效阻抗模型還包括采樣時鐘速率和占空比,那么很小的阻抗變化就可能使數學計算變得異常困難。
還應注意,這些值是ADC內部電路在跟蹤模式下采樣過程(即對信號進行實際采樣)中的反映。在保持模式下,采樣開關斷開,輸入前端電路與內部采樣處理或緩沖器隔離。
推導該簡單模型(圖8)并求解實部和虛部:
Z0 = R, Z1 = 1/s ? C, s = j ? 2 ? π ? f, f = frequency
ZTOTAL = 1/(1/Z0 + 1/Z1) = 1/(1/R + s ? C) = 1/((1 + s ? R ? C)/R)) = R/(1 + s ? R ? C)
代換s并乘以共軛復數:
ZTOTAL = R/(1 + j ? 2 ? π ? f ? R ? C) = R/(1 + j ? 2 ? π ? f ? R ? C) ? ((1 – j ? 2 ? π ? f ? R ? C)/(1 – j ? 2 ? π ? f ? R ? C)) = (R –j ? 2 ? π ? f ? R2 ? C)/(1 + (2 ? π ? f ? R ? C)2)
求出“實部”(Real)和“虛部”(Imag):
ZTOTAL = Real + j ? Imag = R/(1 + (2 ? π ? f ? R ? C)2) + j ? (–2 ? π ? f ? R2 ? C)/(1 + 2 ? π ? f ? R ? C)2)
Real = R/(1 + (2 ? π ? f ? R ? C)2) Imag = (–2 ? π ? f ? R2 ? C)/(1 + (2 ? π ? f ? R ? C)2)
這一數學模型與跟蹤模式下的交流仿真非常吻合(圖9和圖10)。這個簡單模型的主要誤差源是阻抗在高頻時的建立水平。注意,這些值一般是通過一系列仿真得出的,相當準確。
?
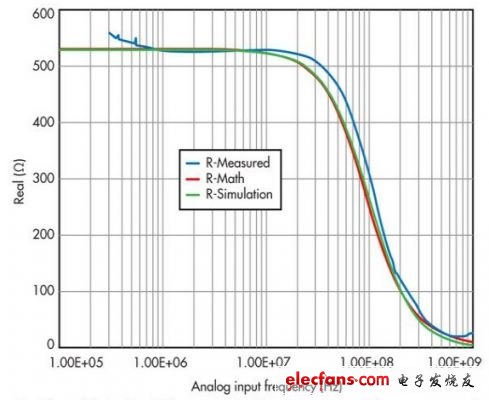
圖9: 顯示的是轉換器輸入阻抗曲線的“實部”部分,它比較了經測量、數學和仿真方法得到的結果。
?
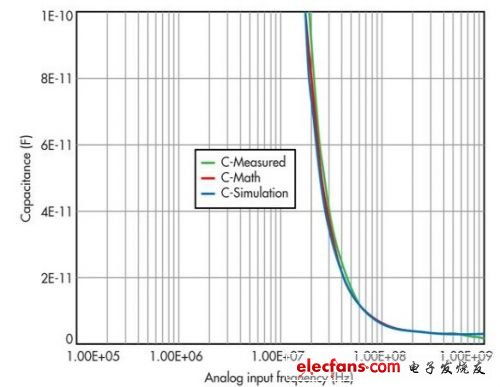
圖10: 顯示的是轉換器輸入阻抗曲線的“虛部”部分,它比較了經測量、數學和仿真方法得到的結果。
現在討論圖9和圖10所示的測量結果。所有三條曲線并不完全重合,但很接近,這是因為某些測量誤差總是存在的,而且仿真可能并未考慮到轉換器的所有封裝寄生效應。因此,一定程度的不一致是正常的。盡管如此,這些曲線在形狀和輪廓方面都很相似,相當近似地給出了轉換器的阻抗特性。
注意,網絡分析儀只能在其特征阻抗標準乘/除10倍的范圍內提供可信的測量結果。如果網絡分析儀的特征阻抗為50Ω,那么只能在5Ω到500Ω的范圍內實現令人滿意的測量。這也是數據手冊中更愿意列出簡單R||C值的原因之一。
ADC輸入阻抗總結
了解轉換器阻抗是信號鏈設計的一個重要內容。總之,若非真正需要,為什么要浪費大筆資金去購買昂貴的測試設備,或者費力去測量阻抗?不如使用數據手冊提供的RC并聯組合阻抗并稍加簡單計算,這種獲取轉換器阻抗曲線的方法更快捷、更輕松。
 電子發燒友App
電子發燒友App











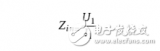










評論