引言
智能儀表的模擬輸入通道一般由傳感器、前置放大電路、有源濾波器、采樣保持電路(S/H)、A/D轉(zhuǎn)換器和微機系統(tǒng)等電路組成[1]。由于電子元器件性能參數(shù)的離散性、穩(wěn)定性和溫度敏感性等問題,目前還得不到根本的解決。因此,從傳感器到A/D 轉(zhuǎn)換之間的任何一個環(huán)節(jié)都存在非線性的問題,使得A/D轉(zhuǎn)換值n與被測量x不成線性關系,即n≠ax+b(a、b為常數(shù))[2]。如果不解決這種非線性問題,將會嚴重影響智能儀表的測量精度。常用的非線性校正方法有校正函數(shù)法、查表法和模型校正法[s]。
① 校正函數(shù)法要求傳感器的輸入/輸出特性能用數(shù)學解析式表示,且輸入通道的其它環(huán)節(jié)可認為是線性的。事實上,很多傳感器的輸入/輸出特性很難用解析式表示,并且如果解析式計算太復雜,還會嚴重影響測量速度。因此,校正函數(shù)法的應用受到較大的局限[4]。
② 查表法必須針對每一個傳感器進行校正,而且需要把大量的校正數(shù)據(jù)制成表格存入儀表內(nèi)存。而一般的智能儀表的內(nèi)存非常有限;當因故更換傳感器時,需要重新校正、修訂內(nèi)存中的表格數(shù)據(jù),應用起來也非常不方便[5]。
③ 模型校正法的基本原理是設法找到一個近似函數(shù)g1(x)或多個分段近似函數(shù)g1(x)、g2(x)、g3(x)、g4(x)等來代替原函數(shù)f(x)。模型校正法的關鍵是如何求出既能滿足精度要求,又能滿足計算簡單的校正模型。通常校正模型計算太復雜會影響測量速度,所以采用模型校正法進行非線性校正時,往往采用離線處理的方式[6]。
針對智能儀表不便于進行復雜計算、內(nèi)存有限和實時性要求高等特點,在比較了幾種常用的非線性校正方法的基礎上,通過對智能儀表的非線性特性曲線的一般性分析,運用分段直線逼近曲線的方法,給出了一種通用的智能儀表非線性自動校正算法。
1 非線性自動校正算法
采用分段直線方程的非線性校正原理如圖l所示。設儀表的被測量用X表示,儀表中對應的燈D轉(zhuǎn)換值用N表示,則曲線OM表示儀表的非線性特性曲線。現(xiàn)將曲線分成若干段,如果分段點的位置和分段數(shù)選取合適,則每一段曲線可近似看成是一直線段。這樣,曲線OM就可看成是由若干直線段組成。如圖中虛線段AB、BC可分別近似表示曲線AB和曲線BC。
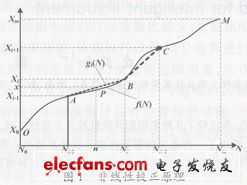
圖1中:曲線OM分段后各段端點對應的被測信號分別為X0, X1,X2,…,Xi-1, Xi, Xi+1,…,Xm;儀表中對應的A/D轉(zhuǎn)換值分別為N0, N1, N2,…,Ni, Ni+1, … ,Nm。其中,x0為被測量的最小值,Xm為被測量的最大值。顯然線段AB的斜率為:
曲線段AB上的點(n,f(n)),可用直線段AB上的點P(n,x)近似表示,而點P滿足:

式(2)、式(3)就是得到的分段直線校正方程。其中式(2)可稱為點斜式校正方程,因為校正方程由線段上的端點(從Ni-1,Xi-1)和斜率ki決定;式(3)可稱為兩點式校正方程,因為校正方程由線段上的兩端點(Ni-1, Xi-1)和(Ni,Xi)決定。
在校準時,若采用點斜式校正方程,則依次把校正方程參數(shù)(Ni-1,Xi-1)和ki(其中i=1,2,3,…,m)存入儀表的內(nèi)存;若采用兩點式校正方程,則依次把校正方程參數(shù)(Ni,Xi)(其中i=0,1,2,3,…,m)存入儀表的內(nèi)存。在實際測量時只要先用程序判斷儀表當前的A/D轉(zhuǎn)換值N位于哪一個直線段,再從儀表內(nèi)存中取出相應直線段的校正方程參數(shù),則可由校正方程求出相應的測量值X。
從校正方程可以看出,測量值只與校正點的測量數(shù)據(jù)有關,而與包括傳感器在內(nèi)的模擬輸入通道的各環(huán)節(jié)的非線性并無直接關系。因此,只要儀表的重復性或穩(wěn)定性較好,即在不同時刻測量同一被測量X時,得到的A/D轉(zhuǎn)換值N始終或基本保持不變,不論非線性是由于傳感器還是因為模擬輸入通道的其它環(huán)節(jié)引起的,都可以達到非線性校正的目的,從而保證儀表的測量精度。理論上講,分的段數(shù)越多,儀表的測量精度就越高,但相應地,占用儀表的內(nèi)存也越多,測量速度也會有少許影響,校準時也會稍微復雜。
需要指出的是,各種智能儀表存在較大的差異,實際應用中要視具體情況對非線性校正方程進行必要的修正。
2 在稱重儀表中的應用
在電子衡器中,廣泛采用的稱重傳感器是壓力或拉力傳感器。不論傳感器的量程多大,其滿度輸出一般為2mV左右,因此,對于同一種類型(靜態(tài)或動態(tài))的電子衡器而言,往往可以采用通用的稱重儀表。
電子衡器尤其是商用電子衡器,不僅對稱重精度有很高的要求,而且對實時性也有較高的要求。因此,稱重儀表的非線性校正必須采用在線方式。
2.1 非線性自動校正方程的修正
在稱重儀表中,最小測量值x0=0kg,對應的零點值N0≠0,而且會隨著環(huán)境溫度的變化而變化,實際測量時,各校正點Xi對應的A/D轉(zhuǎn)換值Ni(i=1,2,3,…)也會因零點的變化而相應發(fā)生變化。也就是說,環(huán)境溫度變化后,實際測量時,當被測量為 Xi時,儀表內(nèi)部獲取的A/D轉(zhuǎn)換值不再是校正時的Ni,從而使得按上述校正方程式(2)或式(3)求取的測量校正值是錯誤的或不準確的。
實驗證明,稱重儀表的零點值N0受環(huán)境溫度的影響較大,而其非線性特性曲線受環(huán)境溫度的影響較小[7]。如圖1中所示,N0發(fā)生變化后,可以近似認為非線性特性曲線OM只是適當左移或右移。也就是說,盡管N0是變化的,而Ni-N0(i=1,2,3,… )可以認為是不變的。
一般來說,每天的不同時刻都會存在一定的溫差,但每天的溫度變化都非常緩慢,稱重儀表的零點在使用過程中的變化也非常緩慢。根據(jù)這個特點,我們完全可以用軟件的方法實現(xiàn)零點跟蹤,即在某個較短的時間段(如0.5s)內(nèi),若采樣到的A/D值n與之前的零點N0之差的絕對值不超過某個較小的數(shù)值,則令N0=n。
鑒于儀表的零點值N0受環(huán)境溫度的影響較大,非線性校正方程要作相應的修正:不管是校正時還是實際測量時,均把得到的A/D轉(zhuǎn)換值減去零點值N0。此時,點斜式校正方程修正為:


























用戶評論
共 0 條評論