微波頻段介電特性的測量具有重要意義，幾種典型需求場景如下：1. 擬基于某介質(zhì)基板材料實現(xiàn)微帶濾波器或諧振器、貼片天線等電路時，需要知曉其介電特性來完成器件/天線的初始設(shè)計，然后通過電磁仿真進行優(yōu)化；2. 機載雷達系統(tǒng)或基站天線系統(tǒng)的天線罩對微波信號的傳輸有一定的影響，產(chǎn)品設(shè)計階段也需要知曉天線罩材料的介電特性，從而評估天線罩對系統(tǒng)性能的可能影響；3. 在室內(nèi)定位、穿墻雷達、移動通信信道建模等情景中，建筑材料的介電特性對微波信號的反射、衰減及時延會影響到應用系統(tǒng)性能，而建筑材料的介電特性及其幾何結(jié)構(gòu)則是影響微波信號的關(guān)鍵參數(shù)，因此也需要評估介電特性。還有許多其它需要評估介電特性的場景，這里不再贅述。

材料的介電特性與通常所說的相對介電常數(shù)有所區(qū)別，一般地，材料介電特性用復介電常數(shù)表示，而相對介電常數(shù)是復介電常數(shù)的實部。實際應用中，出于方便考慮，材料介電常數(shù)通常相對于真空介電常數(shù)進行歸一化（參見《微波電子學——材料電磁參數(shù)的表征與微波測量技術(shù)》公式1.15）：

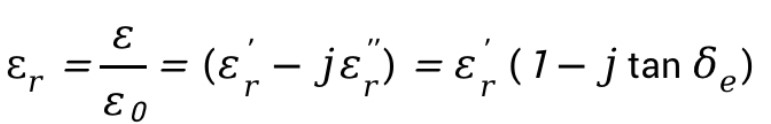
這里，復介電常數(shù)可表示為實部-虛部的形式，也可以用相對介電常數(shù)和損耗正切來表示。從上式可以看出，復介電常數(shù)虛部與損耗正切的關(guān)系為

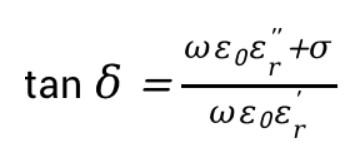
舉例：設(shè)相對介電常數(shù)為4.3、損耗正切為0.025，則復介電常數(shù)虛部為4.3*0.025=0.1075。復介電常數(shù)的虛部通常是指電介質(zhì)中由于偶極子振動阻尼而產(chǎn)生的熱損耗（參見《微波工程》，張肇儀?等譯，第三版8頁）。如果需要考慮材料電導率σ引起的損耗，則可以將電導率并入損耗正切中一并考慮（參見《微波工程》，張肇儀?等譯，第三版9頁）。通常，在電磁仿真軟件中，設(shè)定材料損耗特性時，要么指定損耗正切，要么指定電導率。容易被忽略的一點是：材料介電特性通常與工作頻率有關(guān)。因此，對于窄帶應用系統(tǒng)，需要確準系統(tǒng)工作頻點是否與查閱的材料介電特性頻點相對應，比如查閱的介電參數(shù)對應的頻點是3 GHz，而系統(tǒng)工作頻點是6 GHz，則要考慮查閱的參數(shù)是否適用。對于超寬帶系統(tǒng)而言，則更是需要注意介電參數(shù)對頻率的依賴特性。更詳細的討論可參考相關(guān)電介質(zhì)物理的理論。

盡管有一些理論可以用來預測材料介電參數(shù)，但更為可靠的方法是直接測量材料的介電參數(shù)。材料復介電常數(shù)的測量理論與技術(shù)已經(jīng)發(fā)展和應用了數(shù)十年，盡管已經(jīng)有了非常成熟的技術(shù)和產(chǎn)品，但是這個領(lǐng)域的研究仍是一個重要的課題。一方面，新應用催生的新材料研發(fā)對介電參數(shù)測量技術(shù)提出了越來越高的要求；另一方面，特殊場景（比如高低溫）下的測量需求迫切需要開發(fā)復雜測量系統(tǒng)或者低成本、便攜式測量系統(tǒng)。

總體上而言，材料復介電常數(shù)的測量技術(shù)可以分為2大類：諧振法和非諧振法。前者又可以包括2類方法——諧振器法和諧振器微擾法，后者則可以分為反射法、反射/傳輸法。進一步地，每一類方法又可以采用多種測量夾具，比如非諧振法常用的夾具有同軸線、波導以及喇叭天線等（自由空間法），諧振法常用的夾具有空氣介質(zhì)金屬諧振腔、介質(zhì)諧振腔等。各種測量方法/夾具在適用的頻率范圍、測量精度、對待測樣品形狀尺寸的要求等方面均存在差異，需要依據(jù)具體應用場景、測量成本等因素綜合考慮。

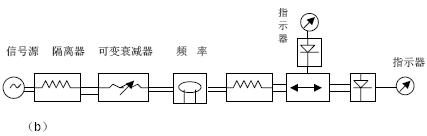
同軸線反射法是非諧振法的代表性方法之一，其成熟產(chǎn)品已經(jīng)獲得了廣泛運用。一種較為常用的測量方法及其理論模型（電容模型）如下圖所示（參見《微波電子學——材料電磁參數(shù)的表征與微波測量技術(shù)》）：

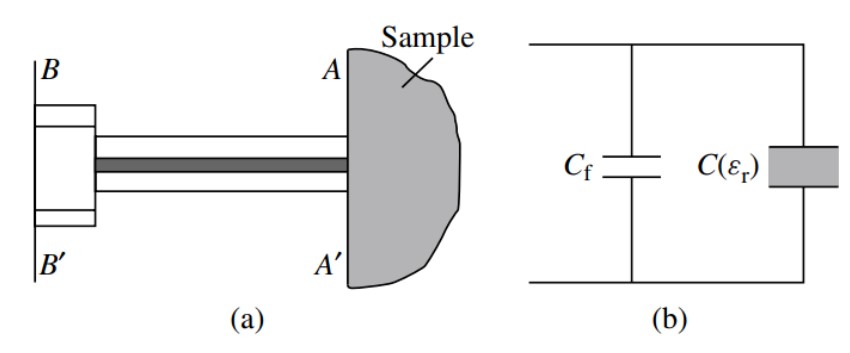
這里，假設(shè)待測樣品為半無限大且與終端開路同軸探針接觸，如上圖a所示；對應的理論模型如圖b所示：總電容由和并聯(lián)構(gòu)成，與樣品介電性能無關(guān)，與樣品介電性能有關(guān)。在平面測得的復反射系數(shù)可以表示為：

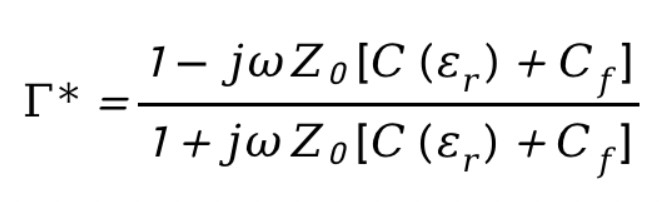
其中，分別包含角頻率、同軸線特征阻抗、同軸線端接空氣時的電容。經(jīng)過對上式進行數(shù)學變換，可以得到復介電常數(shù)的表達式：

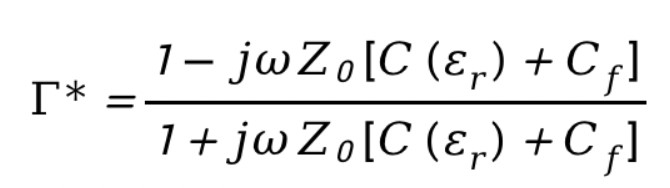
可以通過測量標準樣品獲得兩個電容系數(shù)，比如去離子水（也可以是其它材料）。注意，分別對復反射系數(shù)的實部和虛部求解方程即可獲得系數(shù)和。因此，只需要一個校準樣品。測得標準樣品的反射系數(shù)后，可以采用下式計算兩個電容系數(shù)（Ref.: microwave electronics measurement and materials characterization）：

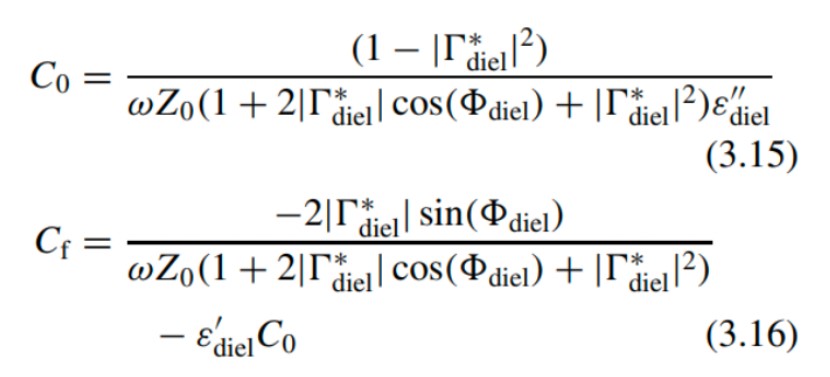
其中，還包含標準樣品的復介電常數(shù)的實部和虛部。

下面以CST仿真實驗來介紹同軸反射法測量介電特性的具體實施方法。首先，設(shè)計特征阻抗為50Ω的空氣介質(zhì)同軸傳輸線，設(shè)計結(jié)果——內(nèi)導體直徑3mm、外導體內(nèi)徑7mm，傳輸線長度理論上不影響特征阻抗，這里任意選取為20mm。仿真中，忽略同軸線導體損耗（亦即設(shè)置為PEC材料）。待測介質(zhì)樣品設(shè)置為立方體，同軸線端接待測介質(zhì)樣品，整體仿真模型如下圖所示。

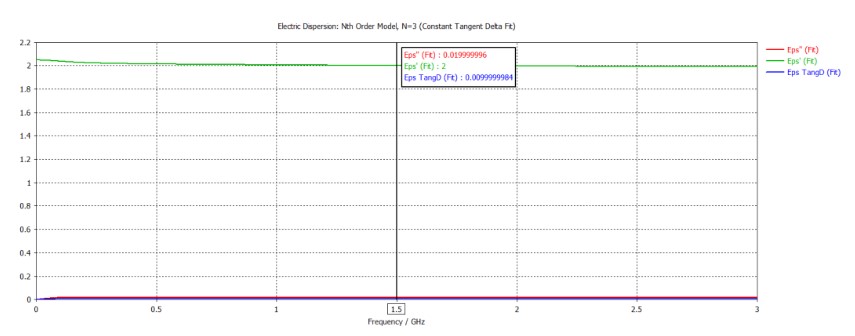
在待測樣品相對介電常數(shù)為2、損耗正切為0.01時（需要留意，在CST仿真中，定義材料損耗正切時，如何考慮色散效應有多種選擇；此處，損耗正切定義頻點為0 GHz、色散模型為Debye模型、擬合階數(shù)為自動設(shè)置亦即采用了“Const. fit - automatic”選項），擬合得到的材料介電特性如下（Eps’是實部、Eps’’是虛部、Eps TanD是損耗正切）。在1.5 GHz處（下文將以此頻點為例，展示介電特性測量過程），擬合得到的材料相對介電常數(shù)為2、損耗正切為0.01，與設(shè)定值吻合。

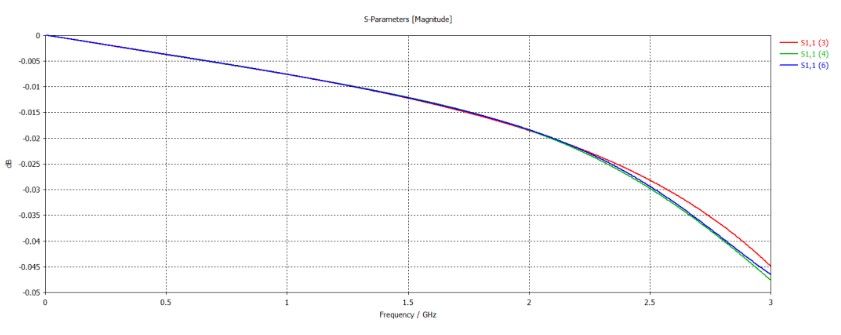
觀察了樣品大小對同軸線S11幅度的影響，所得結(jié)果如下圖（樣品邊長取50、100、200mm，對應S11編號依次為3、4、5）：可以看到當樣品邊長達到100mm時，可以近似認為滿足“半無限大”的假設(shè)。

下圖是樣品大小對S11相位的影響結(jié)果：

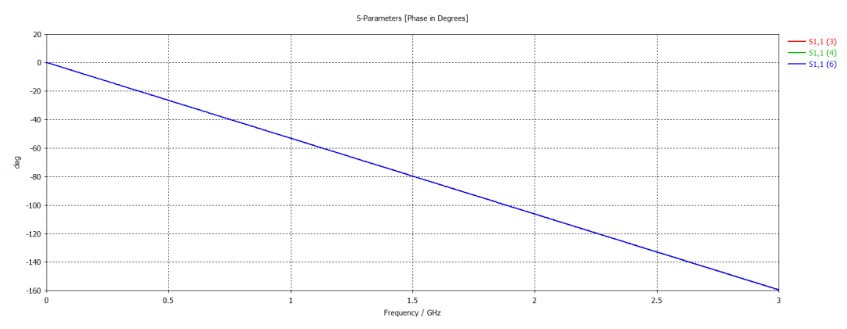
通過上面的仿真，確定待測樣品邊長為100mm。從CST仿真結(jié)果中將S11的幅度和相位數(shù)據(jù)導出，然后換算為復反射系數(shù)，進而得到反射系數(shù)的幅度和相位；同時，需要將標準樣品的相對介電常數(shù)和損耗正切換算為復介電常數(shù)的實部虛部形式；至此，便可利用前述的(3.15)和(3.16)計算系數(shù)兩個點電容系數(shù)。

S11的實部虛部形式如下：

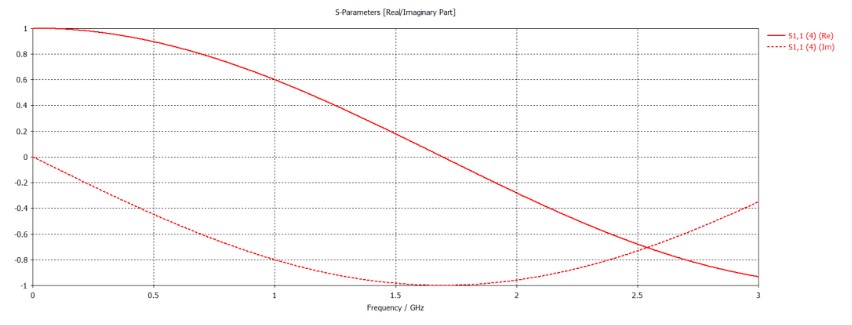
導出的文本格式數(shù)據(jù)如下圖所示（第一列為頻率，第二三列為實部虛部）：

然后，依據(jù)復數(shù)的定義可以得到幅度和相位。

假設(shè)待測樣品相對介電常數(shù)為2.5、損耗正切為0.02，擬合得到的材料參數(shù)如下：

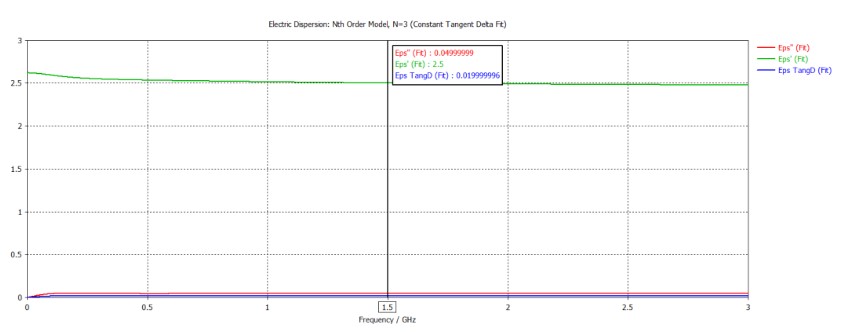
仿真得到其S11，如下圖：

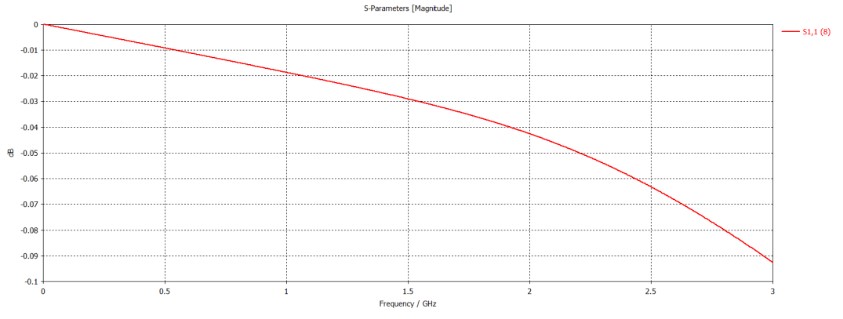
導出復數(shù)反射系數(shù)后，代入前述的復介電常數(shù)計算公式，得到提取出的復介電常數(shù)。這里，以1.5GHz頻點為例進行展示。編寫了如下的MATLAB程序，用于上述的校準和測試結(jié)果參數(shù)提取：

clc;clear;close all;

%% calibration

% input S11 of calibration sample

data01=[1.5000000000000?0.17837039618894?-0.98255058842766];

% frequency

freq=data01(:,1);

% reflection coefficient, equal to S11

Gamma_re=data01(:,2); % real part

Gamma_im=data01(:,3); % imaginary part

Gamma_mag=sqrt(Gamma_re.^2+Gamma_im.^2); % magnitude

Gamma_phase=phase(Gamma_re+1j.*Gamma_im); % phase

% real part of permittivity of calibration sample

ep_sample=2.0;

% loss tangent of calibration sample

loss_sample=0.01;

% imaginary part of permittivity of calibration sample

ep_im_sample=ep_sample*loss_sample;

% angular frequency

omega=2.*pi.*freq*1.5e9;

% characteristic impedance of coaxial line

Z0=50;

% eq.(3.15)

C0=(1-Gamma_mag.^2)./(omega.*Z0.*(1+2.*Gamma_mag.*cos(Gamma_phase)+Gamma_mag.^2).*ep_im_sample);

% eq.(3.16)

Cf=(-2.*Gamma_mag.*sin(Gamma_phase))./(omega.*Z0.*(1+2.*Gamma_mag.*cos(Gamma_phase)+Gamma_mag.^2))-ep_sample.*C0;

%% sample under test

% measured S11 of the sample under test

data02=[1.5000000000000?0.14643780930241?-0.98584447678300];

% frequency

freq02=data02(:,1);

% reflection coefficient, equal to S11?

Gamma_re02=data02(:,2); % real part

Gamma_im02=data02(:,3); % imaginery part

Gamma02=Gamma_re02+1j.*Gamma_im02; % complex form

% solve for complex permittivity of the sample under test

ep_complex_sample02=(1-Gamma02)./(1j.*omega.*Z0.*C0.*(1+Gamma02))-Cf./C0;

ep_sample02_re=real(ep_complex_sample02); % real part

ep_sample02_im=-imag(ep_complex_sample02); % imaginary part

loss_sample02=ep_sample02_im/ep_sample02_re; % loss tangent

上述MATLAB程序的主要工作過程如下：

1.?導入校準樣品的S11亦即反射系數(shù)（這里是仿真得到）

2.?依據(jù)“實部-虛部”形式得到校準樣品反射系數(shù)的幅度和相位

3.?利用校準樣品材料參數(shù)等信息以及校準公式計算C0和Cf

4.?導入待測樣品的S11（這里是仿真得到）

5.?依據(jù)待測材料復介電常數(shù)公式進行計算，得到其實部虛部及損耗正切

最終，MATLAB程序得到的待測樣品相對介電常數(shù)為2.4681、損耗正切為0.02，與設(shè)定的材料參數(shù)吻合（相對介電常數(shù)設(shè)定值為2.5、損耗正切設(shè)定值為0.02）。相對介電常數(shù)誤差為-1.3%。表明前述方法及程序是準確可靠的。

需要指出的是，同軸反射法還有其他模型，此處暫略；此外，由于待測樣品表面可能凹凸不平，導致同軸探頭與待測樣品之間存有空氣間隙，這可能引起測量誤差。后續(xù)有機會再繼續(xù)介紹。


審核編輯：劉清