1、CORDIC 理論

　　1.1、 坐標旋轉數字計算機CORDIC

　　坐標旋轉數字計算機CORDIC(COordinate Rotation DIgital Computer)算法，通過移位和加減運算，能遞歸計算常用函數值，如Sin， Cos，Sinh，Cosh等函數，由J. Volder于1959年提出 ，首先用于導航系統，使得矢量的旋轉和定向運算不需要做查三角函數表、乘法、開方及反三角函數等復雜運算。J. Walther在1974年用它研究了一種能計算出多種超越函數的統一算法 。

　　1.2、CORDIC原理

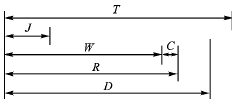
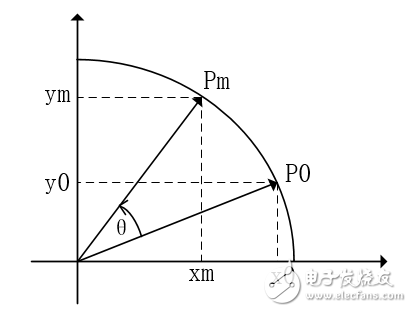
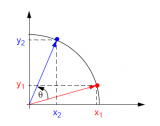
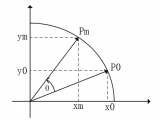
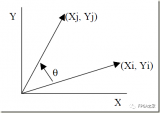
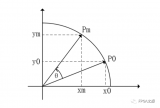
　　如圖所示，初始向量(X(0)，Y(0))旋轉θ角度之后得到向量(X1，Y1)，此向量有如下關系：

　　X1=X0*cos(θ)-Y0*sin(θ)=cos(θ)(X0-Y0*tan(θ))

　　Y1=Y0*cos(θ)+X0*sin(θ)=cos(θ)(Y0+X0*tan(θ))

　　假設初始向量經過N次旋轉之后得到新向量，且每次旋轉角度δ都是正切值為2的倍數，則第i次旋轉角度為δ-arctan(2^(-i))，即cosδ=(1/(1+2^(-2i)))^0.5。

　　容易得到角度θ≈∑S(i)●δ(i)，其中S(i)=1或-1，表示旋轉角度的方向，

　　第i步旋轉可以表示為：

　　X(i+1)=((1/(1+2^(-2i)))^0.5)●(X(i)-S(i)Y(i)2^(-i))

　　Y(i+1)=((1/(1+2^(-2i)))^0.5)●(Y(i)+S(i)X(i)2^(-i))

　　其中(1/(1+2^(-2i)))^0.5)稱為校模因子，當旋轉次數一定時，趨于一個常數，Π(1/(1+2^(-2i)))^0.5)≈0.6073

　　這樣，算法每一步就可以簡化為：

　　X(i+1)=(X(i)-S(i)Y(i)2^(-i))

　　Y(i+1)=(Y(i)+S(i)X(i)2^(-i))

　　從而可以看出，對于移動的角度θ，現在只需要硬件加減法器和移位器就可以算出結果。引入Z，表示i次旋轉后相位累加的部分和，則：

　　Z(i+1)=Z(i)-S(i)arctan(2^(-i))

　　經過n次旋轉之后，Z→0，即與目標角重合，即：

　　X(n)=X1=X0*cos(θ)-Y0*sin(θ)

　　Y(n)=Y1=Y0*cos(θ)+X0*sin(θ)

　　1.3、三角函數的計算

　　以sin/cos計算為例，可利用正/余弦的和角公式遞歸進行：

　　cos(a+b) = cos(a)cos(b) – sin(a)sin(b) = cos(a) [cos(b) – tan(a)sin(b)]

　　sin(a+b) = sin(a)cos(b) + cos(a)sin(b) = cos(a) [tan(a)cos(b) +sin(b)]

　　取a=arctan(2^-k), 即tan(a)=2^-k, 則cos(b) – tan(a)sin(b) 可通過移位和減法來實現。

　　如果角度z可以表示為z = s0 arctan(2^0) + s1 arctan(2^-1) + ... + sn arctan(2^-n), 其 中s0, s1, ..., sn取+1或-1(+1可以理解為逆時針轉角，即加上一個角度; -1則相反) ，那么角度z的sin/cos計算可以通過一系列的移位和加減運算來實現。注意到cos(sk arctan(2^-k))=cos(arctan(2^-k)) 與轉角方向無關。此外，z應取第一項限角度(收斂域)，對於其他項限角度，可由其第一項限對應角度變換得到。

　　相類似地，sinh/cosh的計算利用以下公式：

　　cosh(a+b) = cosh(a)cosh(b) + sinh(a)sinh(b) = cosh(a) [cosh(b) + tanh(a)sinh(b)]

　　sinh(a+b) = sinh(a)cosh(b) + cosh(a)sinh(b) = cosh(a) [tanh(a)cosh(b) + sinh(b)]

　　取a=arctanh(2^-k), 即tanh(a)=2^-k, 則cosh(b) + tanh(a)sinh(b) 可通過移位和減法來實現。如果參數z可以表示為z = s1 arctanh(2^-1) + s2 arctanh(2^-2) + ... + sn arctanh(2^-n), 其 中s1, s2, ..., sn取+1或-1 ，那么z的sinh/cosh計算可以通過一系列的移位和加減運算來實現。

　　z應取[-ln2, ln2]范圍內的值，否則應先預處理 z = z’– pln2, 求得cosh(z’)/sinh(z’)的值，則

　　cosh(z) = cosh(z’)cosh(pln2) + sinh(z’)sinh(pln2) = ?[cosh(z’) + sinh(z’)]2^p + ?[cosh(z’) – sinh(z’)]2^-p

　　sinh(z) = sinh(z’)cosh(pln2) + cosh(z’)sinh(pln2) = ?[cosh(z’) + sinh(z’)]2^p + ?[sinh(z’) – cosh(z’)]2^-p 。

　　sin/cos和sinh/cosh的計算是CORDIC算法的兩個特例，CORDIC算法可描述如下:

　　給定初始值x(0), y(0), z(0),

　　x(k+1) = x(k) – ms(k)y(k)2^-q(m,k), y(k+1) = y(k) + s(k)x(k) 2^-q(m,k), z(k+1) = z(k) – s(k)d(k),

　　其中m表示模式，q(m,k) 為移位序列，s(k) 取+1或-1表示旋轉方向，d(k) 為遞進角度。

　　1.4、CORDIC的MATLAB 運算

　　以cos(a)/sin(a)計算為例，m = 1, x(0) = 1, y(0) = 0, z(0) = a, s(k) = sign(z(k)),移位序列q(1,k): 0, 1, 2, ..., 遞進角度為d(k)=arctan(2^-q(1,k)) 。

　　下面是實現的Matlab程序:

　　z = a;

　　x = 0.6072529350; % scaled cos(0)

　　y = 0; % sin(0)

　　for i = 1:K

　　signZ = sign(z); % s(k) for rotation direction

　　xNew = x - signZ*y*2^(-(i-1));

　　y = signZ*x*2^(-(i-1)) + y;

　　x = xNew;

　　z = z - signZ*atan(2^(-(i-1))); % atan(2^-(i-1)) is included in a look-up table

　　end

　　x的初始值為cos(arctan(1)), cos(arctan(2^-1)), ..., cos(arctan(2^-K) 的連積值，收斂為0.6072529350。

　　以cosh(a)/sinh(a)計算為例，m = -1, x(0) = 1, y(0) = 0, z(0) = a, s(k) = sign(z(k)),移位序列q(-1,k): 1, 2, 3, 4, 4, 5, ... (3n+1重復兩次以保證收斂, 4, 13, 40, ...), 遞進角度為d(k)=arctanh(2^-q(-1,k)) 。

　　通過對初始值和旋轉方向s(k) 的選擇，模式m=0可以計算乘法和除法; 模式m=1可以計算sin/cos/arcsin/arccos/arctan; 模式m=-1可直接計算sinh/cosh/exp/arctanh/ln/sqrt, 間接計算arcsinh/arccosh，參見[1]。

　　2、CORDIC的現實意義

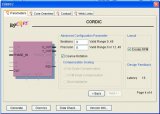
　　由于具有頻率精度高、轉換時間短、頻譜純度高以及頻率相位易編程等特點， 數控振蕩器(NCO)被廣泛應用于軟件無線電數字上、下變頻以及各種頻率和相位數字調制解調系統中。NCO傳統的實現方法主要有查表法、多項式展開法或近似法，但這些方法在速度、精度、資源方面難以兼顧。而采用CORDIC算法來實現超函數時，則無需使用乘法器，它只需要一個最小的查找表(LUT)，利用簡單的移位和相加運算，即可產生高精度的正余弦波形，尤其適合于FPGA的實現。

　　數字控制振蕩器(NCO，numerical controlled oscillator)是軟件無線電、直接數據頻率合成器(DDS，Direct digital synthesizer)、快速傅立葉變換(FFT，Fast Fourier Transform)等的重要組成部分，同時也是決定其性能的主要因素之一，隨著芯片集成度的提高、在信號處理、數字通信領域、調制解調、變頻調速、制導控制、電力電子等方面得到越來越廣泛的應用。