摘要:許多工程師會在設計中遇到一些很微妙的問題:ADC的規格常常低于系統要求的指標。本文介紹了如何根據系統需求合理選擇ADC,列舉了ADC測量中可能遇到的各種誤差源。
采用12位分辨率的模數轉換器(ADC)未必意味著你的系統將具有12位的精度。很多時候,令工程師們吃驚和不解的是:數據采集系統所表現出的性能往往遠低于期望值。如果這個問題直到樣機運行時才被發現,只好慌慌張張地改用更高性能的ADC,大量的時間被花費在重新更改設計上,同時,試投產的日程在迅速臨近。問題出在哪里? 最初的分析中有那些因素發生了改變? 對于ADC的性能指標有一個深入的了解,將有助于發現一些經常導致性能指標不盡人意的細節所在。對于ADC指標的理解還有助于為你的設計選擇正確的ADC。
我們從建立整個系統的性能需求入手,系統中的每個元器件都有相應的誤差,我們的目標是將整體誤差限定在一定的范圍內。ADC是信號通道的關鍵部件,必須謹慎選擇適當的器件。在我們開始評估整體性能之前,假設ADC的轉換效率、接口、供電電源、功耗、輸入范圍以及通道數均滿足系統要求。ADC的精度與幾項關鍵規格有關,其中包括:積分非線性(INL)、失調和增益誤差、電壓基準的精度、溫度效應、交流特性等。最好從直流特性入手評估ADC的性能,因為ADC的交流參數測試存在多種非標準方法,基于直流特性比較容易對兩個IC進行比較。直流特性通常比交流特性更能反映器件的問題。
系統要求
確定系統整體誤差的常見方法有兩種:均方根和(RSS)、最差工作條件下的測試。采用RSS時,對每項誤差取平均,然后求和并計算開方值。RSS誤差由下式計算:
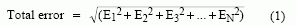
其中EN代表某個特定電路元件或參數的誤差項。當所有誤差不相干時這種方法最準確(實際情況可能如此,也可能不同)。利用最差條件分析法,所有誤差項相加。這種方法能夠確保誤差植不會超出規定范圍,它給出了最差條件下的誤差限制,實際誤差始終小于該值(通常會低出若干倍)。
多數情況下,測量誤差介于兩種方法測試數值之間,更接近于RSS法提供的數值。可以根據誤差預算選擇使用典型誤差和最差工作條件下的誤差。具體選擇時取決于許多因素,包括:測量值的標準方差、特定參數的重要性、誤差之間的相互影響程度等。由此可見,很難找到簡捷的、必需遵循的規則。在我們的分析中,我們選擇最差條件測試法。
在本例中,假定我們需要0.1%或者說10位的精度(1/210),這樣,只有選擇一個具有更高分辨率的轉換器才有意義。如果是一個12位的轉換器,我們可能會想當然地以為精度已足夠高;但是在沒有仔細檢查其規格書之前,我們并沒有把握得到12位的性能(實際情況可能更好或更糟)。舉例來說,一個具有4LSB積分非線性誤差的12位ADC,最多只能提供10位的精度(假設失調和增益誤差已得到修正)。一個具有0.5LSB INL的器件則可提供0.0122%的誤差或13位的精度(消除了增益及失調誤差以后)。要計算最佳精度,可用最大INL誤差除以2N,其中N是轉換器位數。在我們的舉例中,若采用0.075%誤差(或11位)的ADC,則留給其余電路的誤差余量只有0.025%,這其中包括傳感器、前端信號調理電路(運放、多路復用器等等),或許還有數模轉換器(DAC)、PWM信號或信號通路上的其它模擬電路。
我們假設整體系統的總計誤差預算基于信號通道各個電路元件的誤差項目總和,另外我們還假設,將要測量的是一個緩慢變化的直流、雙極性輸入信號,具有1kHz的帶寬,工作溫度范圍為0°C到70°C,并在0°C至50°C范圍內保證性能。
直流性能
微分非線性
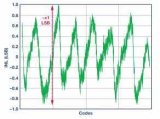
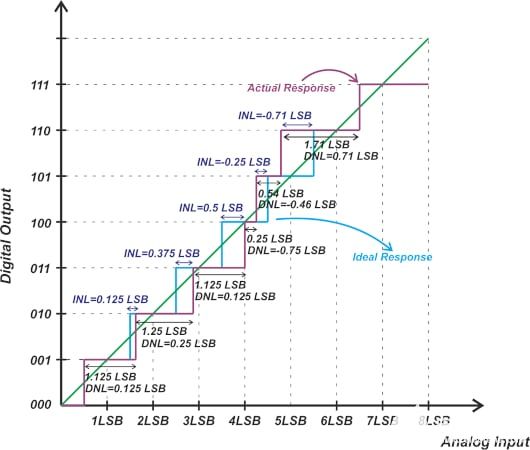
雖說不被作為一項關鍵性的ADC參數,微分非線性(DNL)誤差還是進入我們視野的第一項指標。DNL揭示了一個輸出碼與其相鄰碼之間的間隔。這個間隔通過測量輸入電壓的幅度變化,然后轉換為以LSB為單位后得到(圖1)。值得注意的是INL是DNL的積分,這就是為什么DNL沒有被我們看作關鍵參數的原因所在。一個性能優良的ADC常常聲稱“無丟碼”。這就是說當輸入電壓掃過輸入范圍時,所有輸出碼組合都會依次出現在轉換器輸出端。當DNL誤差小于±1LSB時就能夠保證沒有丟碼(圖1a)。圖1b、圖1c和圖1d分別顯示了三種DNL誤差值。DNL為-0.5LSB時(圖1b),器件保證沒有丟碼。若該誤差值等于-1LSB (圖1c),器件就不能保證沒有丟碼,值得注意的是10碼丟失。然而,當最大DNL誤差值為±1時,大多數ADC都會特別聲明是否有丟碼。由于制造時的測試界限實際上要比規格書中所規定的更為嚴格,因此這種情況下通常都能夠保證沒有丟碼。對于一個大于-1LSB (圖1d中為-1.5LSB)的DNL,器件就會有丟碼。
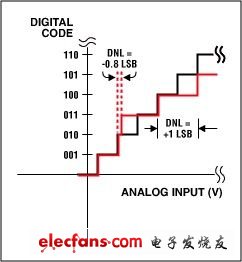
圖1a. DNL誤差:沒有丟碼。

圖1b. DNL誤差:沒有丟碼。

圖1c. DNL誤差:丟失10碼。

圖1d. DNL誤差:AIN*數字輸入是三種可能數值之一,掃描到輸入電壓時,10碼將會丟失。
隨著DNL誤差值的偏移(也就是說-1LSB,+2LSB),ADC轉換函數會發生變化。偏移了的DNL值理論上仍然可以沒有丟碼。關鍵是要以-1LSB作為底限。值得注意的是DNL在一個方向上進行測量,通常是沿著轉換函數向上走。將造成碼[N]跳變所需的輸入電壓值和碼[N+1]時相比較。如果相差為1LSB,DNL誤差就為零。如果大于1LSB,則DNL誤差為正值;如果小于1LSB,DNL誤差則為負值。
有丟碼并非一定是壞事。如果你只需要13位分辨率,同時你有兩種選擇,一個是DNL指標≤ ±4LSB的16位ADC (相當于無丟碼的14位),價格為5美元,另一個是DNL ≤ ±1LSB的16位ADC,價格為15美元,這時候,購買一個低等級的ADC將大幅度地節省你的元件成本,同時又滿足了你的系統要求。
積分非線性
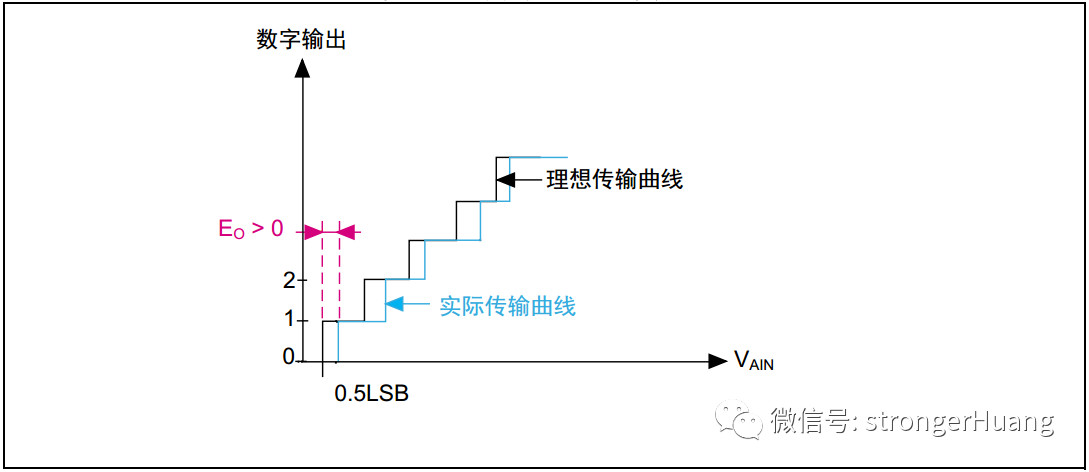
積分非線性(INL)定義為DNL誤差的積分,因此較好的INL指標意味著較好的DNL。INL誤差告訴設計者轉換器測量結果距離理想轉換函數值有多遠。繼續我們的舉例,對于一個12位系統來講,±2LSB的INL誤差相當于2/4096或0.05%的最大非線性誤差(這已占去ADC誤差預算的2/3)。因此,有必要選用一個1LSB (或更好)的器件。對于±1LSB的INL誤差,等效精度為0.0244%,占ADC誤差預算的32.5%。對于0.5LSB的指標,精度為0.012%,僅占ADC誤差預算的16% (0.0125%/0.075%)。需要注意的是,無論是INL或DNL帶來的誤差,都不太容易校準或修正。
失調和增益誤差
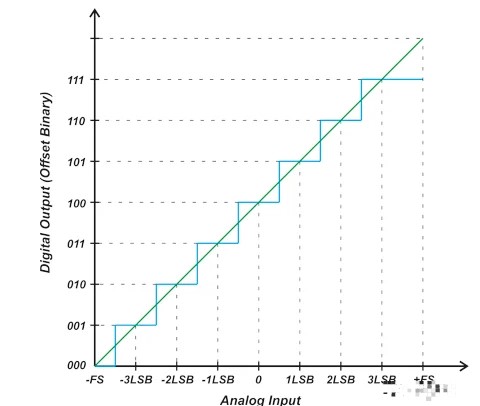
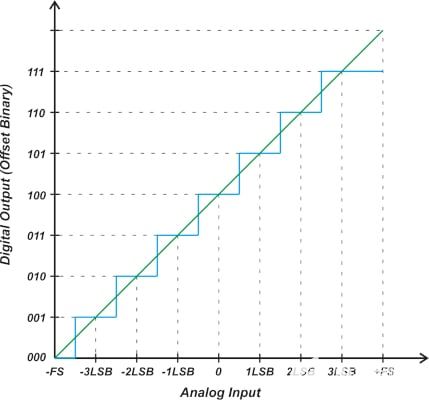
失調和增益誤差很容易利用微控制器(μC)或數字信號處理器(DSP)修正過來。就失調誤差來講,如果轉換器允許雙極性輸入信號的話,操作將非常簡單。對于雙極性系統,失調誤差只是平移了轉換函數,但沒有減少可用編碼的數量(圖2)。有兩套方法可以使雙極性誤差歸零。其一,你可以將轉換函數的x或y軸平移,使負滿度點與單極性系統的零點相對準(圖3a)。利用這種方法,可以簡單地消除失調誤差,然后,通過圍繞“新”零點旋轉轉換函數可以對增益誤差進行調節。第二種技術采用了一種迭代法。首先給ADC輸入施加一個0V電壓并執行一次轉換;轉換結果反映了雙極性零點失調誤差。然后,通過圍繞負滿度點旋轉轉換曲線實現增益調節(圖3b)。注意此時轉換函數已繞A點轉過一定角度,使零點偏離了期望的轉換函數。因此還需要進一步的失調誤差校正。
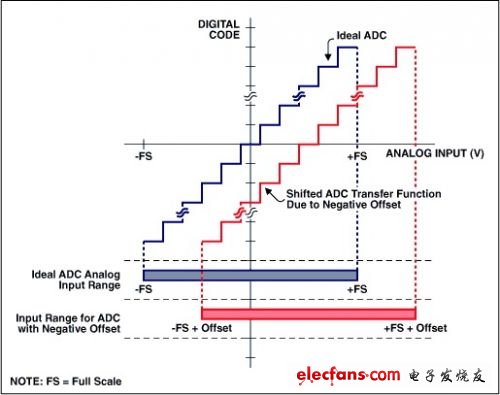
圖2. 雙極性系統的失調誤差
圖3a和3b. 校正雙極性失調誤差(注意:階梯狀轉換函數已被一條直線取代,因為該圖中包含所有碼,而臺階已經小得無法分辨,看上去成為一條直線)。

圖3a和3b. 校正雙極性失調誤差(注意:階梯狀轉換函數已被一條直線取代,因為該圖中包含所有碼,而臺階已經小得無法分辨,看上去成為一條直線)。
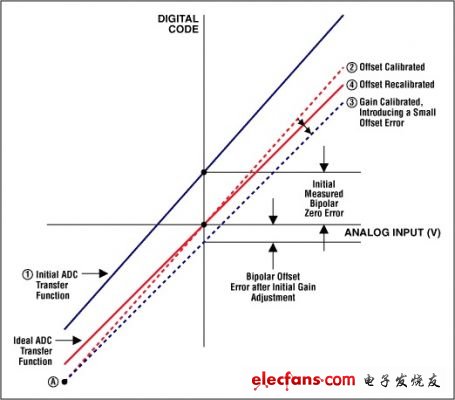
圖3a和3b. 校正雙極性失調誤差(注意:階梯狀轉換函數已被一條直線取代,因為該圖中包含所有碼,而臺階已經小得無法分辨,看上去成為一條直線)。
單極性系統還要復雜一些。如果失調為正值,可采用和雙極性系統相似的處理方法。不同之處在于你將失去一部分ADC量程(見圖4)。如果失調為負值,你將無法簡單地通過一次轉換測得失調誤差。因為在零點以下,轉換器只能顯示出零。這樣,對于一個負失調誤差的轉換器,你必須緩慢地增加輸入電壓,以確定在什么地方ADC結果出現首次跳變。同樣,你將失去一部分ADC量程。
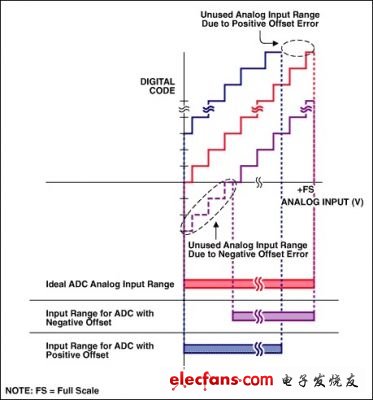
圖4. 單極性系統中的失調誤差
回到我們的舉例,兩種情況中的失調誤差可按下述方法獲得:
2.5V基準時+8mV的失調誤差相當于12位ADC具有13LSB的誤差(8mV/[2.5V/4096])。雖然分辨率仍是12位,但是你必須從每次轉換結果中扣除13個碼以補償失調誤差。值得注意的是,實際上這時的可測量滿量程值就變為了2.5V(4083/4096) = 2.492V。此范圍以上的任何值都會使ADC溢出。因此,ADC的動態范圍或者說輸入范圍減小了。這個問題在較高分辨率的ADC中尤為顯著;在16位系統中,8mV對應于210LSB (VREF = 2.5V)。
如果失調為-8mV (假設為單極性輸入),接近于零的小信號輸入將不會引起任何輸出變化,一直到模擬輸入增加到+8mV 。這同樣造成了ADC動態范圍的減小。
增益誤差定義為滿量程誤差減去失調誤差(圖5)。滿量程誤差在轉換函數曲線上最后一次ADC跳變處進行測量,并和理想ADC的轉換函數相比較。增益誤差可通過軟件用一個簡單的線性函數y = (m1/m2)(x)進行簡單的校正,其中的m1是理想轉換函數的斜率,m2是實際測得的轉換函數的斜率(圖5)。

圖5. 失調、增益和滿量程誤差
增益誤差指標中可能包含或不含ADC參考電壓對于誤差的貢獻。在電氣規范中,檢查一下增益誤差的測試條件,并決定采用內部或外部基準工作是非常重要的。一般情況下,當采用片內基準時增益誤差會比較大。如果增益誤差為零,在對滿量程模擬輸入作轉換時轉換結果應為全1 (對于本例的12位系統則為3FFh) (見圖6) 。由于我們的轉換器不理想,全1轉換結果可能會在施加的輸入電壓大于滿量程(負增益誤差)或小于滿量程(正增益誤差)時出現。有兩種辦法可以調整增益誤差,其一是調節參考電壓,以便在某特定參考電壓下得到滿量程輸出,或者在軟件中采用一個線性校正曲線改變ADC轉換函數的斜率(一階線性方程或查表法)。

圖6. 增益誤差降低了動態范圍
和失調誤差一樣,增益誤差也會降低動態范圍。舉例來說,如果滿量程輸入電壓時轉換得到的數碼輸出為4050而非理想的4096 (12位轉換器),也就是所謂的負增益誤差,在這種情況下,高端的46個碼將無法利用。類似地,如果滿量程數碼4096出現在輸入電壓低于滿量程時,ADC的動態范圍同樣被降低了(見圖6)。值得注意的是對于正的滿量程誤差,你無法在轉換結果變為全1的點之外對轉換器進行校準。
對付失調和增益誤差最簡單的辦法就是找一個誤差值足夠低的ADC,這樣你就不必再考慮校正了。找到一個失調和增益誤差小于4LSB的12位ADC并不困難。
其它誤差源
碼沿噪聲
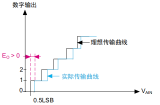
碼沿噪聲是在轉換函數中恰好發生編碼跳變時出現的噪聲。通常在規格書中對該項特性不作規定。甚至對于較高分辨率的轉換器(16位以上),由于更小的LSB間隔,碼沿噪聲更為顯著,通常都對這項性能未作規定。很多時候,碼沿噪聲能有幾個LSB。轉換恰好位于代碼邊緣的模擬輸入時,代碼會在LSB位發生跳動。如果出現明顯的碼沿噪聲,就應該對采樣進行平均,這樣可以有效地從轉換結果中去除這種噪聲。需要對多少個采樣取平均? 如果碼沿噪聲為2/3LSB RMS,這接近于4LSB P-P。那么要將噪聲降低到1LSB,則需要對16次采樣取平均(性能的改進正比于采樣數的均方根)。
基準
采用內部或外部基準的ADC的一個最大潛在誤差源是參考電壓。很多情況下,內置于芯片內部的基準通常都沒有足夠嚴格的規格。為了理解基準所帶來的誤差源,有必要特別關注一下三項指標:溫漂,電壓噪聲,和負載調整。
溫漂
溫漂是規格書中最容易被忽視的一項指標。下面的舉例可以說明溫度漂移是如何影響ADC性能的(圖7)。對于一個12位轉換器,要在整個擴展級溫度范圍(-40°C至+85°C)內保持精度,最大允許的溫漂為4ppm/°C。不幸的是,沒有任何一個ADC包含有這樣高性能的片內基準。如果我們放松要求,將溫度范圍限制于10°C以內,那么12位ADC的參考電壓最多允許25ppm/°C的溫度漂移,這對于片內基準來講仍然是相當嚴格的要求。即便進行多次樣機測試也不能發現這種誤差的嚴重性,因為所采用的元件通常都來自于同一批次。這樣,測試結果不能反映規格書中的極端情況,這主要是由于制造工藝的變化而導致。
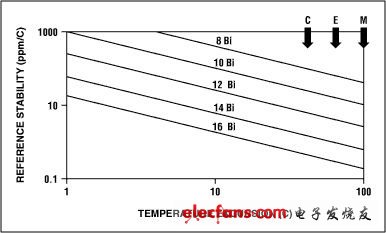
圖7. 電壓基準溫漂要求和ADC分辨率的關系
對有些系統來講,參考電壓的精度不是一個大問題,因為溫度被保持于恒定,避免了溫度漂移問題。還有一些系統采用一種比例測量方式,用同一個信號激勵傳感器和作為參考電壓,可以消除基準引起的誤差(圖8)。因為激勵源和基準同時漂移,漂移誤差相互抵消。
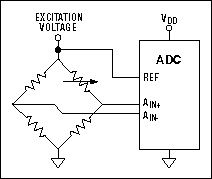
圖8. 比例式ADC轉換
在其它系統中,采用補償手段消除基準漂移通常也很有效。另外也有一些系統并不關注絕對精度,而注重于相對精度。這樣的系統允許基準隨著時間緩慢漂移,同時又能夠提供期望的精度。
電壓噪聲
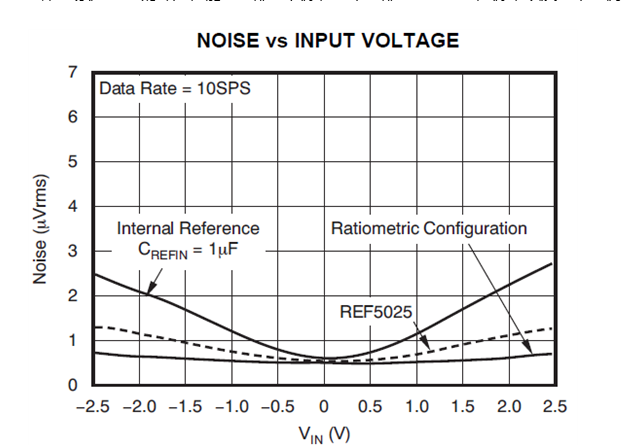
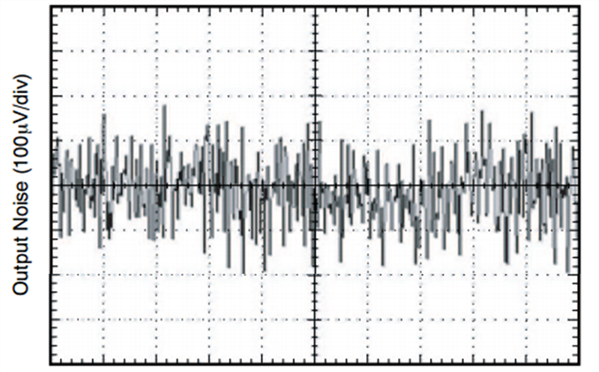
另外一個重要指標是電壓噪聲。它通常規定為RMS值或峰–峰值。要估計它對于性能的影響,需要將RMS值轉換為峰–峰值。如果一個2.5V基準在輸出端具有500μV的峰–峰電壓噪聲(或83μV RMS),該噪聲會帶來0.02%的誤差,或將系統性能限制于僅12位,而且這還沒考慮任何其它的轉換器誤差。理想情況下,基準的噪聲應該遠低于一個LSB ,這樣才不至于限制ADC的性能發揮。帶有片內基準的ADC通常都不規定電壓噪聲,這樣就將確定誤差的任務留給了用戶。如果你的設計沒有達到預期性能,而你又正在使用內置基準,可嘗試采用一個高性能的外部基準,這樣你就可以確定造成性能下降的真正元兇是否是內部基準。
負載調整
最后一項指標是基準的負載調整。用于ADC的電壓基準通常具有足夠的電流可用于驅動其它器件,因此有時也被其它IC使用。其它元件的吸取電流會影響到電壓基準,也就是說隨著吸取電流的增大,參考電壓會跌落。如果使用基準的器件被間歇性地打開和關閉,將會導致參考電壓隨之上升或下降。如果一個2.5V基準的負載調整率指標為0.55μV/μA,那就意味著當有另外一個器件吸取800μA電流時,參考電壓將會改變多達440μV,這將帶來0.0176%的誤差(440μV/2.5V),或占去現有誤差余量的幾乎20%。
其它溫度效應
接下來繼續討論溫度相關的問題,另外還有兩項指標通常很少有人關注,那就是失調漂移和增益漂移。這兩項指標一般只給出典型數值,用戶只能自己判斷它是否足以滿足系統要求。失調和增益的漂移可采用多種不同方法加以補償。一個辦法是仔細測出失調和增益漂移的完整數據,并在存儲器中建立一個表格,然后隨著溫度的變化調節測量值。然而,這是一項繁重的任務,因為每個ADC必須單獨補償,而且補償工序非常費時。第二個辦法是只在溫度發生顯著變化時才執行校準。
對于那些只作一次性溫度校準的系統,需要重點留意一下漂移指標。如果已校準了初始失調但溫度又發生了改變,因漂移的關系又會引入新的誤差,這使校準的效果被減弱。例如,假設在溫度X下進行了一次轉換。隨后的某個時間,溫度變化了10°C,又作了完全相同的另一次測量。兩次讀取的轉換結果會有差異,這會使用戶對系統的可重復性也就是可靠性產生懷疑。
有很多原因促使制造商沒有給出最大界限。其中之一便是成本的增加。漂移測試需要特殊的平臺,并且還要在測試流程中增加額外的工序(這將導致額外的制造成本),以確保所有器件不超出最大漂移界限。
增益漂移的問題更多,尤其是對于那些采用內部基準的器件。這時候,基準的漂移可以一并包含于增益漂移參數中。當采用外部基準時,IC的增益漂移一般比較小,比如0.8ppm/°C。這樣,±10°C的溫度變化將會造成±8ppm的漂移。舉例來講,12位性能等價于244ppm (1/4096 = 0.0244% = 244ppm)。因此,±8ppm的漂移所造成的誤差遠低于12位系統中的一個LSB。
交流特性
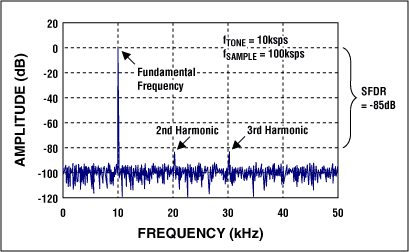
有些ADC只在輸入信號接近于直流時能很好地工作。另外一些則能很好地處理從直流到Nyquist特頻率的信號。僅有DNL和INL符合系統要求并不能說明轉換器能夠同樣合格地處理交流信號。DNL和INL是在直流測試的。要掌握其交流性能就必須了解交流指標。在產品規格書中有電氣參數表和典型工作特性,從中你可以找到有關交流性能的線索。需要考察的關鍵指標有信號–噪聲比(SNR),信號–噪聲加失真比(SINAD),總諧波失真(THD),以及無雜散動態范圍(SFDR)。首先我們來看一看SINAD或SNR。SINAD定義為輸入正弦波信號的RMS值與轉換器噪聲的RMS值(從直流到Nyquist特頻率,包括諧波[總諧波波失真]成分)。諧波發生于輸入頻率的倍數位(圖9)。SNR類似于SINAD,只是它不包含諧波成分。因此,SNR總是好于SINAD。SINAD和SNR一般以dB為單位。

其中N是轉換器的位數。對于理想的12位轉換器,SINAD為74dB。這個方程可重寫為N的表達式,新的表達式揭示了能夠獲得的信息的位數與RMS噪聲的函數關系:

這個方程就是等效位數的定義,即ENOB。
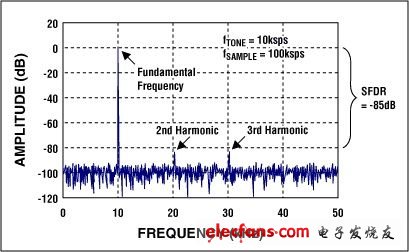
圖9. FFT圖顯示出ADC的交流性能
值得注意的是SINAD和輸入頻率有關。隨著頻率向Nyquist上限逼近,SINAD逐漸下降。如果規格書中的指標是在相對于Nyquist頻率較低的頻率下測得,在接近Nyquist頻率時性能有可能變得很差。在規格書中的典型工作特性中可以找到ENOB曲線,可以觀察到隨著頻率的增加ENOB下降,主要是由于隨著輸入頻率的增加THD逐漸變差。例如,如果在感興趣的頻率SINAD的最小值為68dB,那么你可獲得的ENOB值為11。也就是說,由于轉換器的噪聲和失真,你丟失了1位信息。這也意味著你的12位轉換器最多只能達到0.05%的精度。記住INL是一項直流指標;ENOB是一項有關轉換器對于交流信號的非線性性能指標。
SNR是不考慮失真成分的信號–噪聲比。SNR反映了轉換器的噪聲背景。隨著輸入頻率的增加SNR可能會急劇下降,這說明該轉換器不是為該頻率的應用而設計。改善SNR的一個辦法是過采樣,這種方法提供了一定的處理增益。過采樣以遠高于信號頻率的速度進行采樣,以此來降低轉換器的噪聲背景。這種方法將噪聲譜擴展到更寬的頻域內,這樣就有效降低了一定頻段內的噪聲。兩倍率的過采樣可將噪聲背景降低3dB。
SFDR定義為FFT圖中,頻域內輸入正弦波的RMS值與最高的雜散信號的RMS值之比,一般以dB為單位。對于某些要求ADC動態范圍盡可能大的通信應用,SFDR尤為重要。雜散信號妨礙了ADC對于小輸入信號的轉換,因為失真信號可能會比有用信號大很多。這就限制了ADC的動態范圍。頻域內出現一個大的雜散信號可能對SNR不會有明顯影響,但會顯著影響SFDR。
小結
回到我們一開始的ADC舉例,假設我們將要測量直流型的信號,并且要求ADC可接受雙極性輸入信號,我們選擇B檔的MAX1241,它具有1LSB的DNL誤差,1LSB的DNL誤差(0.0244%),3LSB的失調誤差(3/4096 = 0.0732%),以及4LSB的增益誤差(0.0977%)。所有誤差相加,我們得到總誤差為0.1953%。我們可以校正失調和增益誤差,使總誤差下降到0.0244%。只要參考電壓誤差低于0.075% - 0.024% = 0.051%,就不會突破我們的誤差預算。5ppm/°C的溫漂系數在50°C的溫度范圍內會產生0.025%的漂移誤差,這樣還剩下0.026%的誤差余量。要得到12位的性能,我們需要選用一個電壓噪聲指標低于1LSB的電壓基準(這相當于2.5V/4096 = 610μV峰峰值或102μV RMS值)。溫度系數5ppm/°C,寬帶電壓噪聲30μV RMS的MAX6166是一個很好的選擇。它還具有充足的供出及吸納電流的能力,足以驅動ADC (和其它電路)。30μV噪聲指標等價于180μV峰峰值,只有12位級別下一個LSB的三分之一,11位級別下(我們系統的實際要求)一個LSB的六分之一。
再檢查一下MAX1241的增益漂移,資料顯示該項指標為0.25ppm/°C,50°C溫度范圍內為12.5ppm,能夠很好地滿足我們的設計要求。
現在,我們就得到了一個可行的方案,再也不會出現由于對規格的考慮不周而造成的性能折扣。在本例中我們沒有涉及交流性能。然而,正確理解ADC的技術指標,以及它們如何對轉換器的性能產生作用,無疑將使你具備足夠的知識,能夠從眾多產品中選擇出滿足你性能要求的適當的ADC。
 電子發燒友App
電子發燒友App















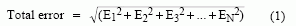










評論