混凝土材料斷裂的聲發射自相似性識別特征
????? 摘要 將對材料聲發射的研究,力學過程的研究,同對材料斷裂損傷等破壞過程的研究相結合,提出了聲發射過程的概念。給出定量考察聲發射過程的自相似性特征函數。并在此基礎上,根據混凝土試塊的三點彎曲試驗,確定出了混凝土試塊斷裂的聲發射自相似性識別特征。
????? 關鍵詞 混凝土材料,斷裂,聲發射過程,自相似性,識別特征???
????? 1 引 言
實驗結果表明,象混凝土這類多裂隙、多相變復合材料,其受力后的聲發射往往是同時有多個聲發射源產生,這樣,所測得的聲發射信號是多個聲發射源信號的疊加。因此,用信號分析的方法來建立力學過程同聲發射參數間的關系非常困難,對于原信號的捕捉和追蹤則近乎不可能。所以,至今為止,聲發射同力學過程間的關系的研究仍只停留在定性分析的水平上。
混凝土內部同時含有許多不同性質的缺陷、裂紋及微觀構造上的不均勻性,混凝土材料的斷裂過程實質上是一個由原生裂隙到微裂紋擴展,最后出現宏觀斷裂的連續過程。而斷裂力學是以主裂紋的開裂作為材料斷裂的判別依據,因此,當采用斷裂力學理論解決混凝土的斷裂問題時,一個很重要的問題,就是如何確定臨界條件,即在上述連續過程中取哪一狀態為開裂的臨界狀態。
本文一改僅僅把聲發射視為信號來分析的做法,在給出聲發射過程定義的基礎上,提出從非線性的角度來尋找力學過程同聲發射參數間的關系。給出了自相似特征函數。并通過試驗,分析了混凝土試塊在三點彎曲過程中聲發射過程自相似性的演化規律,進而得出了混凝土斷裂臨界狀態的聲發射自相似性識別特征。本文的工作,旨在使對聲發射的研究同對力學過程與材料破壞過程的研究有機地結合起來,為混凝土材料的斷裂機理研究提供一條新的思路,為聲發射技術在混凝土結構的穩定性評價及破壞預報方面的應用提供定量依據。
????? 2 聲發射過程的概念
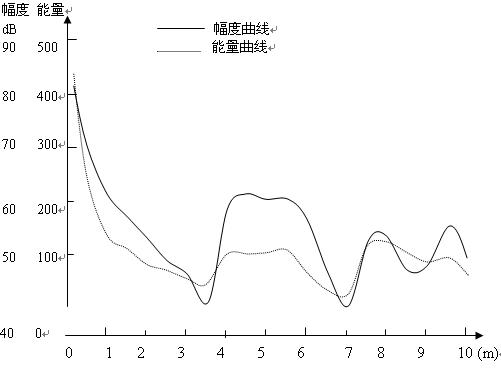
混凝土試塊(規格為7cm×7cm×7cm,配合比為水泥∶砂∶石∶水=1∶1.6∶3.2∶0.6, 最大骨料粒徑1cm)在單軸壓縮時測得的聲發射率及聲發射釋能率兩個參數試驗結果。不同參數在不同狀態下,其值的大小表現出很大的隨機性與離散性。
材料的聲發射過程,通常表現為聲發射參數的序列。如果設材料在一個力學過程中,在時刻t聲發射參數x取某一值的概率為e,那么,材料的聲發射過程可以表示為一個隨機過程,即
????? x=X(e, t) (e∈Ω,t∈T)
????? 式中:x——聲發射參數;
e——與狀態t相對應的概率值,0≤e≤1;
T——過程總延續時間;
Ω——概率空間;
t——試驗時間。也可以是相對應力水平或相對應變水平,當然,此時的T便為材料的極限相對應力或極限相對應變。
就混凝土材料而言,在某一狀態下聲發射參數取某一值的概率e同時受到許多因素的影響,即同時是許多隨機變量的函數。這里,概率e可以表示成
????? e=f(m, t, h, c, …)
????? 式中:m——材料本身的特性參數;
t——溫度;
h——濕度;
c——實驗條件,等等。
顯然,由于這諸因素的多變性、隨機性、模糊性以及彼此之間的相關性,欲尋求某一準確的表達式來確定這一概率是很難的,或者根本是不可能的。然而作為一種非線性過程,由于是材料在荷載作用下內部結構演化的伴生過程,它就必然同時包含了力學過程和材料演化過程的有關特性。因此,我們可以根據材料的結構特點,通過材料的力學試驗,從非線性學科的角度來考察和探討聲發射過程的非線性特征。下面根據試驗,對混凝土材料聲發射過程的自相似性進行討論。
????? 3 聲發射過程的自相似特征函數
自相似性是指事物或現象經過若干步細分變小之后,再將每一部分放大,使其與原事物比較,二者仍然是“相象”的,即指局部與整體在形態、功能和信息等方面是相似的。
不同聲發射過程或同一過程不同狀態下,不同聲發射參數的測試結果既有明顯的區別,又有某種相似性。已有實驗證明,聲發射序列不僅在時域上的分布是分形的,而且聲發射事件在空間上的分布也具有分形特征[4],具有分形特征也就說明聲發射過程具有自相似特征。
為了定量描述混凝土材料不同聲發射過程及聲發射過程不同階段的自相似程度,考察聲發射過程自相似性的演變規律,需先建立自相似特征函數。
聲發射過程或聲發射狀態之間的自相似程度可以用自相似函數來表示。對于聲發射基本參數序列X={xi}, i=1, 2, …,n,可將其按一定的時間間隔(應力水平)劃分為m(m≤n)個時間區域,而將每個時間區域里的聲發射基本參數序列段所表示的聲發射行為,如最大聲發射率、最大振幅、平均聲發射率、平均振幅、聲發射計數等算出。這樣就得到一個容量為m的樣本
????? Y={yi} i=1, 2, …,m
然后,先取Y中的前r個元素來構成r維的“嵌入空間”,得矢量z1,即
????? z1={y1,y2,…,yr}
之后,隨時間滑移,每滑移一個數據得一個矢量,這樣可求出所有的矢量zk:
zk={yk,yk+1,…,yk+r-1}
k=1, 2, …,m-r+1
取前s個zk值,依次計算出(zi+zj)之間的距離dij,其中i, j=1, 2, …,k。給定自相似比1=1/ε,ε為給定的標度,計算有多少個點對之間的距離小于ε,并求出這些點對占總點對的比例c。這樣不斷改變ε值,可計算出介于0和1之間的若干組c(ε)值,則可計算出自相似系數μs。對于h個εj, j=1, 2, …,h,則定義
????? 式中:∑表示從j=1到j=h求和;
其中,μ為Heaviside函數,其定義為
????? 這樣,可根據μs的大小來判斷兩個過程或兩個狀態的相似程度。
混凝土試塊在單軸壓縮情況下聲發射過程自相似系數隨相對應力水平變化情況。可以看出,在不同應力水平上,聲發射過程的自相似程度是不一樣的。因此,若選取適當的r和s,可使自相似系數成為聲發射狀態出現異常的識別特征。
????? 系數隨相對應力水平的變化
????? 4 混凝土材料斷裂過程中聲發射過程自相似性的變化特征
為了研究混凝土斷裂過程中的聲發射自相似特征,進行了中間有切口的混凝土梁的三點彎曲實驗。
試件尺寸為4cm×8cm×28cm,配合比為水泥∶砂∶石子∶水=1∶1.35∶3.15∶0.55,試塊成型后24h脫模,之后在20°C的水中浸泡7d,而后放置在標準養護室中養護至28d。試塊中部預制有深4cm的切口,實驗前用鋼鋸將切口端部鋸尖,采用連續加載的方式。試驗過程中,在進行聲發射檢測的同時,用千分表測出梁中心點處的豎向位移。聲發射檢測設置總增益100dB, 其中前放40dB, 主放60dB,設置門檻值32dB。
????? 聲發射參數在不同應力水平下自相似系數的變化曲線
當相對應力水平達到65%左右時,聲發射事件計數曲線突然上升,位移急劇增大,此時,試塊達到斷裂的臨界狀態[6]。在該應力水平上自相似系數出現最小值,之后又逐漸回升。試塊的臨界斷裂就發生在從最小值向上回升的過程當中。因此,聲發射過程自相似系數的最小值,預示著宏觀斷裂的來臨。我們把材料在臨界斷裂狀態下所表現出的聲發射自相似性模式表達為“最小-回升”型。
????? 5 結 論
(1) 可以認為材料所受的力學過程及材料內部結構的演化過程,是遵循著同一種演化機制的非線性過程,并可以用聲發射來研究。
(2) 利用所建立的自相似特征函數可以對聲發射過程或聲發射過程中不同狀態的自相似程度進行定量描述。
(3) 試驗結果表明,混凝土試塊在三點彎曲過程中,相應聲發射過程不同狀態下的自相似程度是不一樣的,即聲發射過程的自相似程度隨著應力狀態的變化而變化。聲發射過程自相似系數的最小值,預示著宏觀斷裂的來臨。所以,混凝土試塊在臨界斷裂狀態下所表現出的聲發射自相似性識別模式為“最小-回升”型。
混凝土材料斷裂的聲發射自相似性識別特征
發布日期:2007-04-07 09:17:42
????? 摘要 將對材料聲發射的研究,力學過程的研究,同對材料斷裂損傷等破壞過程的研究相結合,提出了聲發射過程的概念。給出定量考察聲發射過程的自相似性特征函數。并在此基礎上,根據混凝土試塊的三點彎曲試驗,確定出了混凝土試塊斷裂的聲發射自相似性識別特征。
????? 關鍵詞 混凝土材料,斷裂,聲發射過程,自相似性,識別特征???
????? 1 引 言
實驗結果表明,象混凝土這類多裂隙、多相變復合材料,其受力后的聲發射往往是同時有多個聲發射源產生,這樣,所測得的聲發射信號是多個聲發射源信號的疊加。因此,用信號分析的方法來建立力學過程同聲發射參數間的關系非常困難,對于原信號的捕捉和追蹤則近乎不可能。所以,至今為止,聲發射同力學過程間的關系的研究仍只停留在定性分析的水平上。
混凝土內部同時含有許多不同性質的缺陷、裂紋及微觀構造上的不均勻性,混凝土材料的斷裂過程實質上是一個由原生裂隙到微裂紋擴展,最后出現宏觀斷裂的連續過程。而斷裂力學是以主裂紋的開裂作為材料斷裂的判別依據,因此,當采用斷裂力學理論解決混凝土的斷裂問題時,一個很重要的問題,就是如何確定臨界條件,即在上述連續過程中取哪一狀態為開裂的臨界狀態。
本文一改僅僅把聲發射視為信號來分析的做法,在給出聲發射過程定義的基礎上,提出從非線性的角度來尋找力學過程同聲發射參數間的關系。給出了自相似特征函數。并通過試驗,分析了混凝土試塊在三點彎曲過程中聲發射過程自相似性的演化規律,進而得出了混凝土斷裂臨界狀態的聲發射自相似性識別特征。本文的工作,旨在使對聲發射的研究同對力學過程與材料破壞過程的研究有機地結合起來,為混凝土材料的斷裂機理研究提供一條新的思路,為聲發射技術在混凝土結構的穩定性評價及破壞預報方面的應用提供定量依據。
????? 2 聲發射過程的概念
混凝土試塊(規格為7cm×7cm×7cm,配合比為水泥∶砂∶石∶水=1∶1.6∶3.2∶0.6, 最大骨料粒徑1cm)在單軸壓縮時測得的聲發射率及聲發射釋能率兩個參數試驗結果。不同參數在不同狀態下,其值的大小表現出很大的隨機性與離散性。
材料的聲發射過程,通常表現為聲發射參數的序列。如果設材料在一個力學過程中,在時刻t聲發射參數x取某一值的概率為e,那么,材料的聲發射過程可以表示為一個隨機過程,即
????? x=X(e, t) (e∈Ω,t∈T)
????? 式中:x——聲發射參數;
e——與狀態t相對應的概率值,0≤e≤1;
T——過程總延續時間;
Ω——概率空間;
t——試驗時間。也可以是相對應力水平或相對應變水平,當然,此時的T便為材料的極限相對應力或極限相對應變。
就混凝土材料而言,在某一狀態下聲發射參數取某一值的概率e同時受到許多因素的影響,即同時是許多隨機變量的函數。這里,概率e可以表示成
????? e=f(m, t, h, c, …)
????? 式中:m——材料本身的特性參數;
t——溫度;
h——濕度;
c——實驗條件,等等。
顯然,由于這諸因素的多變性、隨機性、模糊性以及彼此之間的相關性,欲尋求某一準確的表達式來確定這一概率是很難的,或者根本是不可能的。然而作為一種非線性過程,由于是材料在荷載作用下內部結構演化的伴生過程,它就必然同時包含了力學過程和材料演化過程的有關特性。因此,我們可以根據材料的結構特點,通過材料的力學試驗,從非線性學科的角度來考察和探討聲發射過程的非線性特征。下面根據試驗,對混凝土材料聲發射過程的自相似性進行討論。
????? 3 聲發射過程的自相似特征函數
自相似性是指事物或現象經過若干步細分變小之后,再將每一部分放大,使其與原事物比較,二者仍然是“相象”的,即指局部與整體在形態、功能和信息等方面是相似的。
不同聲發射過程或同一過程不同狀態下,不同聲發射參數的測試結果既有明顯的區別,又有某種相似性。已有實驗證明,聲發射序列不僅在時域上的分布是分形的,而且聲發射事件在空間上的分布也具有分形特征[4],具有分形特征也就說明聲發射過程具有自相似特征。
為了定量描述混凝土材料不同聲發射過程及聲發射過程不同階段的自相似程度,考察聲發射過程自相似性的演變規律,需先建立自相似特征函數。
聲發射過程或聲發射狀態之間的自相似程度可以用自相似函數來表示。對于聲發射基本參數序列X={xi}, i=1, 2, …,n,可將其按一定的時間間隔(應力水平)劃分為m(m≤n)個時間區域,而將每個時間區域里的聲發射基本參數序列段所表示的聲發射行為,如最大聲發射率、最大振幅、平均聲發射率、平均振幅、聲發射計數等算出。這樣就得到一個容量為m的樣本
????? Y={yi} i=1, 2, …,m
然后,先取Y中的前r個元素來構成r維的“嵌入空間”,得矢量z1,即
????? z1={y1,y2,…,yr}
之后,隨時間滑移,每滑移一個數據得一個矢量,這樣可求出所有的矢量zk:
zk={yk,yk+1,…,yk+r-1}
k=1, 2, …,m-r+1
取前s個zk值,依次計算出(zi+zj)之間的距離dij,其中i, j=1, 2, …,k。給定自相似比1=1/ε,ε為給定的標度,計算有多少個點對之間的距離小于ε,并求出這些點對占總點對的比例c。這樣不斷改變ε值,可計算出介于0和1之間的若干組c(ε)值,則可計算出自相似系數μs。對于h個εj, j=1, 2, …,h,則定義
????? 式中:∑表示從j=1到j=h求和;
其中,μ為Heaviside函數,其定義為
????? 這樣,可根據μs的大小來判斷兩個過程或兩個狀態的相似程度。
混凝土試塊在單軸壓縮情況下聲發射過程自相似系數隨相對應力水平變化情況。可以看出,在不同應力水平上,聲發射過程的自相似程度是不一樣的。因此,若選取適當的r和s,可使自相似系數成為聲發射狀態出現異常的識別特征。
????? 系數隨相對應力水平的變化
????? 4 混凝土材料斷裂過程中聲發射過程自相似性的變化特征
為了研究混凝土斷裂過程中的聲發射自相似特征,進行了中間有切口的混凝土梁的三點彎曲實驗。
試件尺寸為4cm×8cm×28cm,配合比為水泥∶砂∶石子∶水=1∶1.35∶3.15∶0.55,試塊成型后24h脫模,之后在20°C的水中浸泡7d,而后放置在標準養護室中養護至28d。試塊中部預制有深4cm的切口,實驗前用鋼鋸將切口端部鋸尖,采用連續加載的方式。試驗過程中,在進行聲發射檢測的同時,用千分表測出梁中心點處的豎向位移。聲發射檢測設置總增益100dB, 其中前放40dB, 主放60dB,設置門檻值32dB。
????? 聲發射參數在不同應力水平下自相似系數的變化曲線
當相對應力水平達到65%左右時,聲發射事件計數曲線突然上升,位移急劇增大,此時,試塊達到斷裂的臨界狀態[6]。在該應力水平上自相似系數出現最小值,之后又逐漸回升。試塊的臨界斷裂就發生在從最小值向上回升的過程當中。因此,聲發射過程自相似系數的最小值,預示著宏觀斷裂的來臨。我們把材料在臨界斷裂狀態下所表現出的聲發射自相似性模式表達為“最小-回升”型。
????? 5 結 論
(1) 可以認為材料所受的力學過程及材料內部結構的演化過程,是遵循著同一種演化機制的非線性過程,并可以用聲發射來研究。
(2) 利用所建立的自相似特征函數可以對聲發射過程或聲發射過程中不同狀態的自相似程度進行定量描述。
(3) 試驗結果表明,混凝土試塊在三點彎曲過程中,相應聲發射過程不同狀態下的自相似程度是不一樣的,即聲發射過程的自相似程度隨著應力狀態的變化而變化。聲發射過程自相似系數的最小值,預示著宏觀斷裂的來臨。所以,混凝土試塊在臨界斷裂狀態下所表現出的聲發射自相似性識別模式為“最小-回升”型。
 電子發燒友App
電子發燒友App





















評論