描述
最近在做特征級別的感知結果融合算法。我的工作目的,是要將多種不同傳感器的感知結果,通過一定的機制融合起來,得到融合后的感知結果。
為此看了一些資料,了解到Apollo中使用了匈牙利匹配算法,之前不懂就學習了一下。
創建ROS工作環境
匈牙利算法(Hungarian Algorithm),該算法的核心就是尋找增廣路徑,它是一種用增廣路徑求二分圖最大匹配的算法,是一種能夠在多項式時間內解決分配問題的組合優化算法。
網上有些作者比喻得很貼切,一句話先簡單理解下匈牙利算法吧:有100個男人和100個女人,使用匈牙利算法可以湊出更多的夫妻(一男一女…)。
為了更深的理解算法是如何運行的,我們需要補充一些圖論知識:比如,什么是二分圖,什么又是增廣矩陣,等等。(圖論中非相關知識自行學習)
二、算法所需的圖論知識
二分圖
一個圖中的所有頂點可劃分為兩個不相交的集合 U 和 V ,使得每一條邊都分別連接U、V中的頂點。如果存在這樣的劃分,則此圖為一個二分圖,又稱二部圖。
“這個二分圖可以理解為某個世界,在該世界中人非男即女。那么每個人其實都是這個圖中的一個頂點,男人集合和女人集合彼此割裂,男人就是男人,女人就是女人,男人可以和女人結合,這實際上就是一個二分圖。”
匹配
二分圖中的一個匹配,就是此時二分圖中一些邊的集合,這個邊集合中的任意兩條邊沒有公共的頂點,也構不成一個圈。
“100個男人和100個女人組成的二分圖中,如果可以任意結婚,那么就會有很多種結婚組合。我們把其中的一種結婚組合的可能性,稱為一次匹配。在這次匹配中,任意一對夫妻都是合法夫妻,沒有任何性別的第三者存在哈哈。”
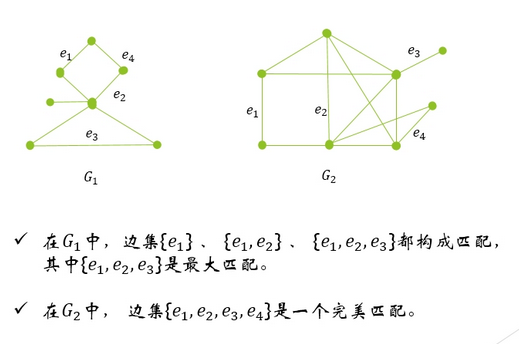
最大匹配
一個圖的所有匹配中,所含匹配邊數最多的匹配,稱為這個圖的最大匹配。最大匹配數,就是最大匹配時邊的數目。
“100個男人和100個女人,在平行時空下肯定有很多種結婚的組合啊,也就是有很多種匹配。
那么,在所有匹配中,結婚對數最多的那次匹配,就是這個二分圖的最大匹配。匈牙利算法是個月老和丘比特,他的目標就是要湊出最多的新人”
完美匹配
如果一個圖的某個匹配中,所有的頂點都是匹配點,那么它就是一個完美匹配。
顯然,完美匹配一定是最大匹配(完美匹配的任何一個點都已經匹配,添加一條新的匹配邊一定會與已有的匹配邊沖突)。但并非每個圖都存在完美匹配。
“100個男人和100個女人,每個男人都和一個女人結婚了,而且他們都是沒有重婚罪的合法夫妻,這就是這個圖的完美匹配。顯然,這是一次最大匹配了。
如果100個男人和99個女人構成的二分圖,即使匈牙利算法再厲害,也還是會有個單身狗,并不存在完美匹配。”
三、算法原理
匈牙利算法有兩個重要概念,先介紹一下。
交錯路徑
給定圖G的一個匹配M,如果一條路徑的邊交替出現在M中和不出現在M中,我們稱之為一條M-交錯路徑。
增廣路徑
如果一條M-交錯路徑,它的兩個端點都不與M中的邊關聯,我們稱這條路徑叫做M-增廣路徑。增廣路徑有一個重要特點:非匹配邊比匹配邊多一條。
我畫了一幅圖,我們有一幅8個頂點構成的圖G。其中有一種匹配,是圖中的黑線表示的2和4兩條邊,這兩條邊加上8個頂點,構成了圖G的一種匹配M。

為了方便理解,我將圖中的8個頂點按照二分圖進行劃分,綠色點表示男人,黃色點表示女人。
顯然匹配M的意思就是,8個人中,由邊2和邊4代表的兩對男女結成了夫妻。
按照交錯路徑的概念,1234、2345、12345都是M-交錯路徑(123456都不是,因為5和6均不在匹配M中,01234同理),而在這三個交錯路徑中,只有12345才是M-增廣路徑。那么,找出匹配M的增廣路徑意義合在呢?
我們會發現,在路徑12345中,還存在著另外一種匹配1、3、5,它的匹配數是3,要大于匹配M的匹配數2。
那么我們就得到了新的一個匹配N,它比匹配M更優。按照同樣的方式,我們來尋找N-增廣路徑,會發現0123456是匹配N的增廣路徑,它的匹配數是4。
因此圖G的最大匹配,實際上是由0、2、4、6等四條邊構成的匹配。
因此,研究增廣路徑的意義就是改進匹配模式,只要把增廣路徑中的匹配邊和非匹配邊的身份交換就可以了。身份交換后,圖中的匹配邊數目,將比原來增多 1 條。
匈牙利算法的核心,就是通過不斷尋找原有匹配M的增廣路徑,來增加匹配中的匹配邊和匹配點,從而達到該圖下的最大匹配。
四、算法流程
概念
飽和
設一個圖為G,G中一些不相鄰的邊組成了一個集合M,這個集合M就是G的一個匹配。匹配M中的每條邊都有兩個端點,這兩個端點都稱為是M飽和的。
“有一些男人一些女人婚姻關系未明(一個圖G),一些男女結成了夫妻(一種匹配關系M),結婚的男女都算已婚了(M飽和)”
綜上,就把飽和——理解成已婚,比較好理解我下面的分析。
4.1 匈牙利算法單邊飽和

第0步
10個男人,9個女人,怎么飽和?如果10個男人,有10個及以上的女人,存在飽和的可能性,任選一種匹配M,準備去找一個飽和X匹配。
第1步
如果當前匹配M,已經X飽和了,10個男人都匹配了老婆,算法停止;否則,任取一個沒老婆的男人x(取X中一個M非飽和點x),這個男人放進集合S中,并設一個集合T為空集。
集合S中會存儲已經結婚的男人+這個單身狗,集合T是這些男人的已婚配偶。
第2步
如果集合S中的位于匹配頂點的男人,他們可以匹配的女人(頂點的臨接頂點N(S)),全部是已婚配偶(∈T),那么算法停止,當前的圖就是會有男人找不到老婆。
否則,我們找到了一個沒有在當前路徑的女人y(y∈N(S)-T),當然了這個女人可能有老公(也在匹配M中,只不過是不同路徑),也有可能是硬拆散的(算法首次進入第2步,由于集合T為空,會強拆掉一組夫妻),也有可能壓根就是未婚的。
第3步
如果上一步選擇的女人y,她是有老公z的(y是M飽和的,yz∈M)。我們暫時先把他們拆開,老公z放進集合S中,女人y放進集合T中,然后去執行第2步。
去執行第2步,意味著也許也許也許…拆掉現有的一對夫妻,這對夫妻中的老婆能解決之前狼少肉多問題的同時,老公還能找到新的老婆。
否則,如果上一步選擇的女人y,是沒有老公的。我們找到了新的一種結婚方案(一條增廣路P(x,y)),這個方案里讓單身狗x去娶一個已婚的女人,然后原匹配夫妻中每個已婚男人都去娶別人老婆,剩下的一個已婚男人去娶這個小姑娘y。大家都很happy……hahahaha(增廣路取反)
4.2 二部圖最大匹配的匈牙利算法

這里可以自行按照上面的分析,去理解算法。雖然真正理解算法較為困難,也不再這里贅述。
總結
這篇文章清晰明了的介紹了下匈牙利算法。如何與多傳感器融合特征算法相結合,會在以后的文章中介紹。
審核編輯:劉清
 電子發燒友App
電子發燒友App




















評論