在選取Q和R時,主要從以下幾方面考慮:
(1)Q是正定或半正定矩陣,R是正定矩陣。
(2)Q陣中對角線上的元素與狀態變量一一對應,數值越大,則表示該狀態變量對系統的影響越顯著。
(3)加權矩陣R不要過小,否則會導致控制量的增大。控制量太大會超過系統執行機構的能力,R陣也不要太大,否則控制作用太小會影響控制性能。
綜合以上考慮,取Q=diag([100,100,100,100]),R=1,利用Matlab提供的LQR函數,可得控制器的增益矩陣:
K=[-10.000 0 -24.140 8 250.036 0 158.553 3]
3.3 利用遺傳算法優化Q陣
遺傳算法是一種基于生物界中的自然選擇原理和自然遺傳機制的隨機搜索算法,它模擬了生物界中的生命進化機制,并用在人工系統中實現特定目標的優化。
采用遺傳算法優化加權陣Q的具體步驟如下:
(1)選擇編碼策略,把參數轉換成染色體結構空間。
(2)確定解碼方法。
(3)確定優化目標函數的類型及數學描述形式,在LQR最優控制中取目標函數J,J=trace(P)。
(4)設計遺傳算子。
(5)確定遺傳策略。設群體大小為80,最大迭代次數為200,交叉概率選為0.9,變異概率選為0.01,并隨機產生初始群體。
(6)計算群體中的個體或染色體解碼后的適應值。在本設計中將適應值取為目標函數值的倒數,即f=1/J。
(7)進行遺傳算法搜索過程,即采用隨機采樣的方法選擇個體,通過交叉和變異產生新個體,再計算新個體的目標函數值J’。
(8)判斷群體性能是否滿足指標或者是否完成迭代次數,若不滿足則重復步驟(7)。
通過上述算法即可確定使目標函數值最小加權矩陣Q中待優化元素的值,從而確定反饋控制規律的向量K。
4 仿真結果及分析
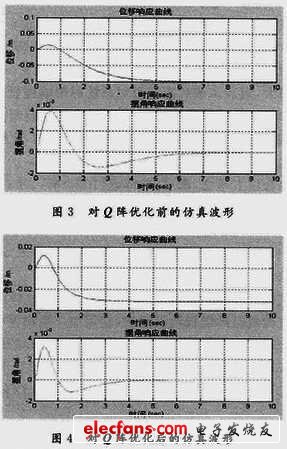
取Q=diag([100,100,100,100]),R=1時,得到的一級倒立擺仿真波形如圖3所示。由圖可見,小車經過5.2 s達到平衡,而擺角經過6.5 s達到平衡。對Q陣優化后系統響應超調量減少,響應速度加快,調節時間減少,系統的靜態特性和動態特性都得到改善,如圖4所示。
5 結語
本文利用拉格朗日方程建立了直線一級倒立擺控制系統的數學模型,在此基礎上分析了該系統的性能,并利用LQR控制器進行控制。結果表明,LQR控制器對該系統具有良好的控制作用。



























用戶評論
共 0 條評論