加法器,加法器是什么意思

加法器 ：
　　加法器是為了實現加法的。
　　即是產生數的和的裝置。加數和被加數為輸入，和數與進位為輸出的裝置為半加器。若加數、被加數與低位的進位數為輸入，而和數與進位為輸出則為全加器。常用作計算機算術邏輯部件，執行邏輯操作、移位與指令調用。
　　對于1位的二進制加法，相關的有五個的量：1，被加數A，2，被加數B，3，前一位的進位CIN，4，此位二數相加的和S，5，此位二數相加產生的進位COUT。前三個量為輸入量，后兩個量為輸出量，五個量均為1位。
　　對于32位的二進制加法，相關的也有五個量：1，被加數A（32位），2，被加數B（32位），3，前一位的進位CIN（1位），4，此位二數相加的和S（32位），5，此位二數相加產生的進位COUT（1位）。
　　要實現32位的二進制加法，一種自然的想法就是將1位的二進制加法重復32次（即逐位進位加法器）。這樣做無疑是可行且易行的，但由于每一位的CIN都是由前一位的COUT提供的，所以第2位必須在第1位計算出結果后，才能開始計算；第3位必須在第2位計算出結果后，才能開始計算，等等。而最后的第32位必須在前31位全部計算出結果后，才能開始計算。這樣的方法，使得實現32位的二進制加法所需的時間是實現1位的二進制加法的時間的32倍。
　　可以看出，上法是將32位的加法1位1位串行進行的，要縮短進行的時間，就應設法使上敘進行過程并行化。
　　逐位進位加法器，在每一位的計算時，都在等待前一位的進位。那么不妨預先考慮進位輸入的所有可能，對于二進制加法來說，就是0與1兩種可能，并提前計算出若干位針對這兩種可能性的結果。等到前一位的進位來到時，可以通過一個雙路開關選出輸出結果。這就是進位選擇加法器的思想。
　　提前計算多少位的數據為宜？同為32位的情況：線形進位選擇加法器，方法是分N級，每級計算32/N位；平方根進位選擇加法器，考慮到使兩個路徑（1，提前計算出若干位針對這兩種可能性的結果的路徑，2，上一位的進位通過前面的結構的路徑）的延時達到相等或是近似。方法，或是2345666即第一級相加2位，第二級3位，第三級4位，第四級5位，第五級6位，第六級6位，第七級6位；或是345677即第一級相加3位，第二級4位，第三級5位，第四級6位，第五級7位，第六級7位。
　　進一步分析加法進行的機制，可以使加法器的結構進一步并行化。
　　令G = AB，P = A⊕B，則COUT（G，P） = G + PCIN，S（G，P）=P⊕CIN。由此，A，B，CIN，S，COUT五者的關系，變為了G，P，CIN，S，COUT五者的關系。
　　再定義點運算（?），（G，P）?（G’，P’）=（G + PG’,PP’），可以分解（G 3：2,P3：2） =（G3，P3）?（G2，P2）。 點運算服從結合律，但不符合交換律。
　　點運算只與G，P有關而與CIN無關，也就是可以通過只對前面若干位G，P進行點運算計算，就能得到第N位的GN：M，PN：M值，當取M為0時，獲得的GN：0，PN：0即可與初使的CIN一起代入COUT（G，P） = G + PCIN，S（G，P）=P⊕CIN，得到此位的COUT，S；而每一位的G，P值又只與該位的A，B值即輸入值有關，所以在開始進行運算后，就能并行的得到每一位的G，P值。
　　以上分析產生了超前進位加法器的思想：三步運算，1，由輸入的A，B算出每一位的G，P；2，由各位的G，P算出每一位的GN：0，PN：0；3，由每一位的GN：0，PN：0與CIN算出每一位的COUT，S。其中第1，3步顯然是可以并行處理的，計算的主要復雜度集中在了第2步。
　　第2步的并行化，也就是實現GN：0，PN：0的點運算分解的并行化。

?加法器定義

實現多位二進制數相加的電路稱為加法器, 它能解決二進制中1＋1＝10 的功能（當然還有 0＋0、0＋1、1＋0）.

加法器的分類

一、半加器概念：能對兩個1位二進制數進行相加而求得和及進位的邏輯電路稱為半加器。或：只考慮兩個一位二進制數的相加，而不考慮來自低位進位數的運算電路，稱為半加器。

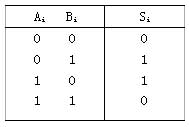
Ai、Bi：加數， Si：本位的和。

二、全加器

概念：能對兩個1位二進制數進行相加并考慮低位來的進位，即相當于3個1位二進制數相加，求得和及進位的邏輯電路稱為全加器。或：不僅考慮兩個一位二進制數相加，而且還考慮來自低位進位數相加的運算電路，稱為全加器。

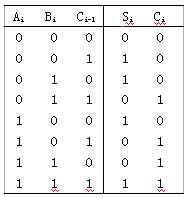
Ai、Bi：加數， Ci-1：低位來的進位，Si：本位的和， Ci：向高位的進位。

加法器的實現

1、串行進位加法器

構成：把n位全加器串聯起來，低位全加器的進位輸出連接到相鄰的高位全加器的進位輸入。

特點：進位信號是由低位向高位逐級傳遞的，速度不高。

2、并行進位加法器（超前進位加法器）

設一個n位的加法器的第i位輸入為ai、bi、ci，輸出si和ci+1，其中ci是低位來的進位，ci+1（i=n-1，n-2，…，1，0）是向高位的進位，c0是整個加法器的進位輸入，而cn是整個加法器的進位輸出。則和 si=ai i i+ ibi i+ i ici+aibici (1)

進位ci＋1=aibi+aici+bici (2)

令gi=aibi， (3)

pi=ai+bi, (4)

則 ci＋1= gi+pici (5)

只要aibi=1，就會產生向i+1位的進位，稱g為進位產生函數；同樣，只要ai+bi=1，就會把ci傳遞到i+1位，所以稱p為進位傳遞函數。把(5)式展開，得到

ci+1= gi+ pigi-1+pipi-1gi-2+…+ pipi-1…p1g0+ pipi-1…p0c0 (6) 隨著位數的增加(6)式會加長，但總保持三個邏輯級的深度，因此形成進位的延遲是與位數無關的常數。一旦進位（c1~cn-1）算出以后，和也就可由（1）式得出。

使用上述公式來并行產生所有進位的加法器就是超前進位加法器。產生gi和pi需要一級門延遲，ci 需要兩級，si需要兩級，總共需要五級門延遲。與串聯加法器（一般要2n級門延遲）相比，（特別是n比較大的時候）超前進位加法器的延遲時間大大縮短了。