兩個二進制數(shù)字A_i，B_i和一個進位輸入C_i相加，產生一個和輸出S_i，以及一個進位輸出C_i＋1。
　　
　　表2.2中列出一位全加器進行加法運算的輸入輸出真值表。

表2.2 一位全加器真值表圖

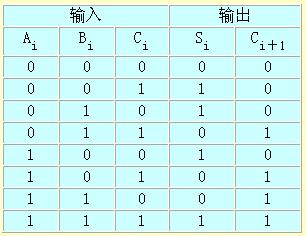
　　根據(jù)表2.2所示的真值表，三個輸入端和兩個輸入端可按如下邏輯方程進行聯(lián)系：
　　
　　S_i＝A_i⊕B_i⊕C_i

??? C_i＋1＝A_iB_i＋B_iC_i＋C_iA_i??????? (2.23)
　　
　　按此表達式組成的一位全加器示圖2.2，求和部分S_i由兩個異或門組成，進位部分C_i+1由與非門組成。

圖2.2　一位全加器(FA)單元

　　補碼運算的二進制加法/減法器的邏輯結構圖

由圖看到，n個1位的全加器(FA)可級聯(lián)成一個n位的行波進位加減器。M為方式控制輸入線，當M＝0時，作加法(A＋B)運算；當M＝1時，作減法(A－B)運算，在后一種情況下，A－B運算轉化成[A]_補＋[－B]_補運算，求補過程由B＋1來實現(xiàn)。因此，圖中最右邊的全加器的起始進位輸入端被連接到功能方式線M上，作減法時M＝1，相當于在加法器的最低位上加1。另外，圖中左邊還表示出單符號位法的溢出檢測邏輯；當C_n＝C_n－1時，運算無溢出；而當C_n≠C_n－1時，運算有溢出，經(jīng)異或門產生溢出信號。
　　
　　對一位全加器(FA)來說，S_i的時間延遲為6T(每級異或門延遲3T)，C_i＋1的時間延遲為5T，其中T被定義為相應于單級邏輯電路的單位門延遲。T通常采用一個“與非”門或一個“或非”門的時間延遲來作為度量單位。
　　
　　現(xiàn)在我們計算一個n位的行波進位加法器的時間延遲。假如采用圖2.2(a)所示的一位全加器并考慮溢出檢測，那么n位行波進位加法器的延遲時間t_a為
　　
　　t_a＝n·2T＋9T＝(2n＋9)T??????? (2.22)
　　
　　9T為最低位上的兩極“異或”門再加上溢出“異或”門的總時間，2T為每級進位鏈的延遲時間。
　　
　　當不考慮溢出檢測時，有
　　
　　t_a＝(n-1)·2T＋9T　　　　　　 　(2.23)
　　
　　t_a意味著加法器的輸入端輸入加數(shù)和被加數(shù)后，在最壞情況下加法器輸出端得到穩(wěn)定的求和輸出所需的最長時間。顯然這個時間越小越好。注意，加數(shù)、被加數(shù)、進位與和數(shù)都是用電平來表示的，因此，所謂穩(wěn)定的求和輸出，就是指穩(wěn)定的電平輸出。