數值分析
2.1微分?
diff函數用以演算一函數的微分項,相關的函數語法有下列4個:??
diff(f) 傳回f對預設獨立變數的一次微分值??
diff(f,'t') 傳回f對獨立變數t的一次微分值??
diff(f,n) 傳回f對預設獨立變數的n次微分值??
diff(f,'t',n) 傳回f對獨立變數t的n次微分值??
?
數值微分函數也是用diff,因此這個函數是靠輸入的引數決定是以數值或是符號微分,如果引數為向量則執行數值微分,如果引數為符號表示式則執行符號微分。??
?
?先定義下列三個方程式,接著再演算其微分項:??
>>S1 = '6*x^3-4*x^2+b*x-5';??
>>S2 = 'sin(a)';??
>>S3 = '(1 - t^3)/(1 + t^4)';??
>>diff(S1)??
ans=18*x^2-8*x+b??
>>diff(S1,2)??
ans= 36*x-8??
>>diff(S1,'b')??
ans= x??
>>diff(S2)??
ans=??
cos(a)??
>>diff(S3)??
ans=-3*t^2/(1+t^4)-4*(1-t^3)/(1+t^4)^2*t^3??
>>simplify(diff(S3))??
ans= t^2*(-3+t^4-4*t)/(1+t^4)^2?
?
2.2積分?
?int函數用以演算一函數的積分項, 這個函數要找出一符號式 F 使得diff(F)=f。如果積
int(f) 傳回f對預設獨立變數的積分值??
int(f,'t') 傳回f對獨立變數t的積分值??
int(f,a,b) 傳回f對預設獨立變數的積分值,積分區間為[a,b],a和b為數值式??
int(f,'t',a,b) 傳回f對獨立變數t的積分值,積分區間為[a,b],a和b為數值式??
int(f,'m','n') 傳回f對預設變數的積分值,積分區間為[m,n],m和n為符號式??
我們示范幾個例子:??
>>S1 = '6*x^3-4*x^2+b*x-5';??
>>S2 = 'sin(a)';??
>>S3 = 'sqrt(x)';?
>>int(S1)??
ans= 3/2*x^4-4/3*x^3+1/2*b*x^2-5*x??
>>int(S2)??
ans= -cos(a)??
>>int(S3)??
ans= 2/3*x^(3/2)??
>>int(S3,'a','b')??
ans= 2/3*b^(3/2)- 2/3*a^(3/2)??
>>int(S3,0.5,0.6)???
ans= 2/25*15^(1/2)-1/6*2^(1/2)??
>>numeric(int(S3,0.5,0.6)) % 使用numeric函數可以計算積分的數值??
ans= 0.0741?
?
2.3求解常微分方程式??
?? MATLAB解常微分方程式的語法是dsolve('equation','condition'),其中equation代表常微分方程式即y'=g(x,y),且須以Dy代表一階微分項y' D2y代表二階微分項y'' ,???
condition則為初始條件。?????
假設有以下三個一階常微分方程式和其初始條件?????
y'=3x2, y(2)=0.5????
y'=2.x.cos(y)2, y(0)=0.25??????
y'=3y+exp(2x), y(0)=3????
對應上述常微分方程式的符號運算式為:??????
>>soln_1 = dsolve('Dy = 3*x^2','y(2)=0.5')??????
ans= x^3-7.500000000000000?????
>>ezplot(soln_1,[2,4]) % 看看這個函數的長相?????
?
>>soln_2 = dsolve('Dy = 2*x*cos(y)^2','y(0) = pi/4')??????
ans= atan(x^2+1)????
>>soln_3 = dsolve('Dy = 3*y + exp(2*x)',' y(0) = 3')??????
ans= -exp(2*x)+4*exp(3*x)???
?
2.4非線性方程式的實根??
??? 要求任一方程式的根有三步驟:???
??? 先定義方程式。要注意必須將方程式安排成 f(x)=0 的形態,例如一方程式為sin(x)=3,
則該方程式應表示為 f(x)=sin(x)-3。可以 m-file 定義方程式。??
??? 代入適當范圍的 x, y(x) 值,將該函數的分布圖畫出,藉以了解該方程式的「長相」。?
??? 由圖中決定y(x)在何處附近(x0)與 x 軸相交,以fzero的語法fzero('function',x0) 即可求出在 x0附近的根,其中 function 是先前已定義的函數名稱。如果從函數分布圖看出根不只一個,則須再代入另一個在根附近的 x0,再求出下一個根。?
?
??? 以下分別介紹幾數個方程式,來說明如何求解它們的根。?
??? 例一、方程式為??
??? sin(x)=0??
??? 我們知道上式的根有 ,求根方式如下:??
>> r=fzero('sin',3) % 因為sin(x)是內建函數,其名稱為sin,因此無須定義它,選擇 x=3 附近求根??
?r=3.1416??
>> r=fzero('sin',6) % 選擇 x=6 附近求根??
r = 6.2832?
?
??? 例二、方程式為MATLAB 內建函數 humps,我們不須要知道這個方程式的形態為何,不過我們可以將它劃出來,再找出根的位置。求根方式如下:??
>> x=linspace(-2,3);??
>> y=humps(x);??
>> plot(x,y), grid % 由圖中可看出在0和1附近有二個根
???>> r=fzero('humps',1.2)??
r = 1.2995?
?
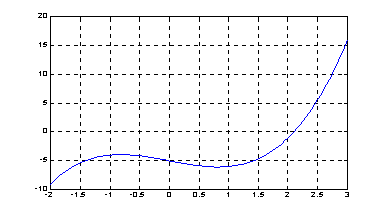
例三、方程式為y=x.^3-2*x-5??
??? 這個方程式其實是個多項式,我們說明除了用 roots 函數找出它的根外,也可以用這節介紹的方法求根,注意二者的解法及結果有所不同。求根方式如下:??
% m-function, f_1.m??
function y=f_1(x) % 定義 f_1.m 函數??
y=x.^3-2*x-5;?
>> x=linspace(-2,3);??
>> y=f_1(x);??
>> plot(x,y), grid % 由圖中可看出在2和-1附近有二個根?
? 

?
?>> r=fzero('f_1',2); % 決定在2附近的根??
r = 2.0946??
>> p=[1 0 -2 -5]??
>> r=roots(p) % 以求解多項式根方式驗證??
r =??
2.0946??
-1.0473 + 1.1359i ??
-1.0473 - 1.1359i??
?
2.5線性代數方程(組)求解
??? 我們習慣將上組方程式以矩陣方式表示如下??
???? AX=B??
其中 A 為等式左邊各方程式的系數項,X 為欲求解的未知項,B 代表等式右邊之已知項?
要解上述的聯立方程式,我們可以利用矩陣左除 \ 做運算,即是 X=A\B。??
??? 如果將原方程式改寫成 XA=B?
其中 A 為等式左邊各方程式的系數項,X 為欲求解的未知項,B 代表等式右邊之已知項?
??? 注意上式的 X, B 已改寫成列向量,A其實是前一個方程式中 A 的轉置矩陣。上式的 X 可以矩陣右除 / 求解,即是 X=B/A。??
??? 若以反矩陣運算求解 AX=B, X=B,即是 X=inv(A)*B,或是改寫成 XA=B, X=B,即是X=B*inv(A)。??
?
??? 我們直接以下面的例子來說明這三個運算的用法:?
?
>> A=[3 2 -1; -1 3 2; 1 -1 -1]; % 將等式的左邊系數鍵入??
>> B=[10 5 -1]'; % 將等式右邊之已知項鍵入,B要做轉置??
>> X=A\B % 先以左除運算求解??
X = % 注意X為行向量??
-2??
5??
6??
>> C=A*X % 驗算解是否正確??
C = % C=B??
?
10??
5??
-1?
>> A=A'; % 將A先做轉置??
>> B=[10 5 -1];??
>> X=B/A % 以右除運算求解的結果亦同??
X = % 注意X為列向量??
10?5?-1??
>> X=B*inv(A); % 也可以反矩陣運算求解?
 電子發燒友App
電子發燒友App






















評論