?如果你是第一次使用Mathematica,那么以下幾點(diǎn)請(qǐng)你一定牢牢記住:
Mathematica中大寫小寫是有區(qū)別的,如Name、name、NAME等是不同的變量名或函數(shù)名。
系統(tǒng)所提供的功能大部分以系統(tǒng)函數(shù)的形式給出,內(nèi)部函數(shù)一般寫全稱,而且一定是以大寫英文字母開頭,如Sin[x],Conjugate[z]等。
乘法即可以用*,又可以用空格表示,如2 3=2*3=6 ,x y,2 Sin[x]等;乘冪可以用“^”表示,如x^0.5,Tan[x]^y。
自定義的變量可以取幾乎任意的名稱,長度不限,但不可以數(shù)字開頭。
當(dāng)你賦予變量任何一個(gè)值,除非你明顯地改變?cè)撝祷蚴褂肅lear[變量名]或“變量名=.”取消該值為止,它將始終保持原值不變。
一定要注意四種括號(hào)的用法:()圓括號(hào)表示項(xiàng)的結(jié)合順序,如(x+(y^x+1/(2x)));[]方括號(hào)表示函數(shù),如Log[x],BesselJ[x,1];{}大括號(hào)表示一個(gè)“表”(一組數(shù)字、任意表達(dá)式、函數(shù)等的集合),如{2x,Sin[12 Pi],{1+A,y*x}};[[]]雙方括號(hào)表示“表”或“表達(dá)式”的下標(biāo),如a[[2,3]]、{1,2,3}[[1]]=1。
Mathematica的語句書寫十分方便,一個(gè)語句可以分為多行寫,同一行可以寫多個(gè)語句(但要以分號(hào)間隔)。當(dāng)語句以分號(hào)結(jié)束時(shí),語句計(jì)算后不做輸出(輸出語句除外),否則將輸出計(jì)算的結(jié)果。
一.數(shù)的表示及計(jì)算
1.在Mathematica中你不必考慮數(shù)的精確度,因?yàn)槌悄阒付ㄝ敵鼍龋琈athematica總會(huì)以絕對(duì)精確的形式輸出結(jié)果。例如:你輸入
In[1]:=378/123,系統(tǒng)會(huì)輸出Out[1]:=126/41,如果想得到近似解,則應(yīng)輸入
In[2]:=N[378/123,5],即求其5位有效數(shù)字的數(shù)值解,系統(tǒng)會(huì)輸出Out[2]:=3.073
2,另外Mathematica還可以根據(jù)你前面使用的數(shù)字的精度自動(dòng)地設(shè)定精度。
Mathematica與眾不同之處還在于它可以處理任意大、任意小及任意位精度的數(shù)值,如100^7000,2^(-2000)等數(shù)值可以很快地求出,但在其他語言或系統(tǒng)中這是不可想象的,你不妨試一試N[Pi,1000]。
Mathematica還定義了一些系統(tǒng)常數(shù),如上面提到的Pi(圓周率的精確值),還有E(自然對(duì)數(shù)的底數(shù))、I(復(fù)數(shù)單位),Degree(角度一度,Pi/180),Infinity(無窮大)等,不要小看這些簡單的符號(hào),它們包含的信息遠(yuǎn)遠(yuǎn)大于我們所熟知的它們的近似值,它們的精度也是無限的。
?
二.“表”及其用法
“表”是Mathematica中一個(gè)相當(dāng)有用的數(shù)據(jù)類型,它即可以作為數(shù)組,又可以作為矩陣;除此以外,你可以把任意一組表達(dá)式用一個(gè)或一組{}括起來,進(jìn)行運(yùn)算、存儲(chǔ)。可以說表是任意對(duì)象的一個(gè)集合。它可以動(dòng)態(tài)地分配內(nèi)存,可以方便地進(jìn)行插入、刪除、排序、翻轉(zhuǎn)等等幾乎所有可以想象到的操作。
如果你建立了一個(gè)表,你可以通過下表操作符[[]](雙方括號(hào))來訪問它的每一個(gè)元素,如我們定義table={2,Pi,Sin[x],{aaa,A*I}}為一個(gè)表,那么table[[1]]就為2,table[[2]]就是Pi,而table[[3,1]]表示嵌套在table中的子表{aaa,A*I}的第一個(gè)元素即aaa,table[[3,2]]表示{aaa,A*I}第二個(gè)元素即A*I。總之,表每一層次上并列的部分用逗號(hào)分割,表可以無窮嵌套。
你可以通過Append[表,表達(dá)式]或Prepend[表,表達(dá)式]把表達(dá)式添加到表的最前面或最后面,如Append[{1,2,3},a]表示{1,2,3,a}。你還可以通過Union[表1,表2,......],Jion[表1,表2,......]來把幾個(gè)表合并為一個(gè)表,二者不同在于Union在合并時(shí)刪除了各表中重復(fù)的元素,而后者僅是簡單的合并;你還可以使用Flatten[表]把表中所有子表"抹平"合并成一個(gè)表,而Patition[表,整數(shù)n]把表按每n個(gè)元素分段作為子表,集合成的表。如Flatten[{1,2,{Sin[x],dog},{{y}}}]表示{1,2,Sin[x],y},而Partition[{1,2,Sin[x],y},2]把表每兩個(gè)分段,結(jié)果為{{1,2},{Sin[x],y}};還可以通過Delete[表,位置]、Insert[表,位置]來向表中按位置插入或刪除元素,如要?jiǎng)h除上面提到的table中的aaa,你可以用Delete[table,{3,1}]來實(shí)現(xiàn);Sort[表]給出了表中各元素的大小順序,Reverse[表]、RotateLeft[表,整數(shù)n]、RotateRight[表,整數(shù)n]可以分別將一個(gè)表進(jìn)行翻轉(zhuǎn)、左轉(zhuǎn)n個(gè)元素、右轉(zhuǎn)n個(gè)元素等操作,Length[表]給出了表第一個(gè)層次上的元素個(gè)數(shù),Position[表,表達(dá)式]給出了表中出現(xiàn)該表達(dá)式的位置,Count[表,表達(dá)式]則給出表達(dá)式出現(xiàn)的次數(shù)。各種表的操作函數(shù)還有很多,這里就不再一一介紹了。
?
三.圖形函數(shù)
Mathematica的圖形函數(shù)十分豐富,用寥寥幾句就可以畫出復(fù)雜的圖形,而且可以通過變量和文件存儲(chǔ)和顯示圖形,具有極大的靈活性。
圖形函數(shù)中最有代表性的函數(shù)為Plot[表達(dá)式,{變量,下限,上限},可選項(xiàng)],(其中表達(dá)式還可以是一個(gè)"表達(dá)式表",這樣可以在一個(gè)圖里畫多個(gè)函數(shù));變量為自變量;上限和下限確定了作圖的范圍;可選項(xiàng)可要可不要,不寫系統(tǒng)會(huì)按默認(rèn)值作圖,它表示對(duì)作圖的具體要求。例如Plot[Sin[x],{x,0,2*Pi},AspectRatio-1]表示在0
.二維函數(shù)作圖
Plot[函數(shù)f,{x,xmin,xmax},選項(xiàng)]
在區(qū)間{x,xmin,xmax}上,按選項(xiàng)的要求畫出函數(shù)f的圖形
Plot[{函數(shù)1,函數(shù)2},{x,xmin,xmax},選項(xiàng)]
在區(qū)間{x,xmin,xmax}上,按選項(xiàng)的要求畫出幾個(gè)函數(shù)的圖形?
圖一.用Plot生成x*Sin[1/x]的圖形
.二維參數(shù)畫圖函數(shù)
ParametricPlot[{x[t],y[t]},{t,t0,t1},選項(xiàng)] 畫一個(gè)X軸,Y軸坐標(biāo)為{x[t],y[t]},參變量t在[t0,t1]中的參數(shù)曲線
?
?
.三維函數(shù)作圖
Plot3D[f[x,y],{x,x0,x1},{y,y0,y1},選項(xiàng)]
?
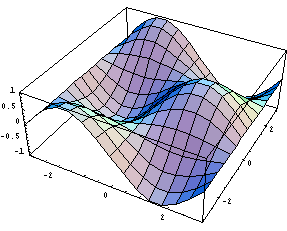
圖3.用Plot3D生成的Sin[x]*Cos[y]的三維圖形
?
除Plot,二維參數(shù)方程作圖的ParametricPlot[{x(t),y(t)},{t,下限,上限},可選項(xiàng)]、三維作圖的Plot3D[二維函數(shù)表達(dá)式,{變量1,下限,上限}, {變量2,下限,上限},可選項(xiàng)}]、三維參數(shù)方程作圖的ParametricPlot3D[{x(u,v),y(u,v),z(u,v)},{u,下限,上限},{v,下限,上限},可選項(xiàng)]外,還有畫二維等高線圖ContourPlot[二元表達(dá)式,{變量1,下限,上限}, {變量2,下限,上限},可選項(xiàng)}]、畫二維密度圖的DensityPlot[二元表達(dá)式,{變量1,下限,上限}, {變量2,下限,上限},可選項(xiàng)}]等等不一而足。
除使用上述函數(shù)作圖以外,Mathematica還可以象其他語言一樣使用圖形元語言作圖,如畫點(diǎn)函數(shù)Point[x,y],畫線函數(shù)Line[x1,y1,x2,y2],畫圓的Circle[x,y,r],畫矩形和多邊形的Rectangle和Polygon,字符輸出的Text[字符串,輸出坐標(biāo)],還有顏色函數(shù)RGBColor[red,green,blue]、Hue[],GrayLevel[gray]來描述顏色的亮度、灰度、飽和度,用PointSize[相對(duì)尺度]、Thickness[相對(duì)尺度]來表示點(diǎn)和線的寬度。總之Mathematica可以精確地調(diào)節(jié)圖形的每一個(gè)特征。
四.數(shù)學(xué)函數(shù)的用法
Mathematica系統(tǒng)內(nèi)核提供了豐富的數(shù)學(xué)計(jì)算的函數(shù),包括極限、積分、微分、最值、極值、統(tǒng)計(jì)、規(guī)劃等數(shù)學(xué)的各個(gè)領(lǐng)域,復(fù)雜的數(shù)學(xué)問題簡化為對(duì)函數(shù)的調(diào)用,極大地提高了解決問題的效率。
Mathematica提供了所有的三角、反三角、雙曲、反雙曲、各種特殊函數(shù)(如貝塞爾函數(shù)系、橢圓函數(shù)等),各種復(fù)數(shù)函數(shù)(如Im[z],Re[z],Conjugate[z], Abs[z],Arg[z]),各種隨機(jī)函數(shù)(如Random[n]可以通過不同的參數(shù)產(chǎn)生任意范圍內(nèi)整型、實(shí)型任意分布的隨機(jī)數(shù)),矩陣運(yùn)算函數(shù)(如求特征值特征向量的EigenVector[],EigenValue[],求逆的Inverse[]等)。
Mathematica還提供了大量數(shù)學(xué)操作的函數(shù),如取極限的Limit[f[x],{x,a}],求微分的D[f[x],x],全微分的Dt[f[x],x],不定積分的Integrate[f[x],x]和定積分的Integrate[f[x],{x,a,b}],解任意方程的Solve[lhs=rhs,x]及微分方程的DSolve[lhs=rhs,x],解冪級(jí)數(shù)和付立葉展開的Series[f[x]],F(xiàn)ourier[f[x]]及其逆變化InverseSeries,InverseFourier, 求和函數(shù)Sum[],求積函數(shù)Product[],以上函數(shù)均可以適用于多維函數(shù)或多維方程。
Mathematica中還有相當(dāng)數(shù)量的數(shù)值計(jì)算函數(shù),最常用的是N[表達(dá)式,整數(shù)]可以求出表達(dá)式精確到指定有效數(shù)字的數(shù)值解,還有如數(shù)值求積分的NIntegrate[],求方程數(shù)值根的NSolve[]和NDSolve[],最小、最大值的NFindMinimum[]和NFindMaximum[]等等。
Mathematica還有各種表達(dá)式操作的函數(shù),如取分子、分母的 Numerator[expr] , Denormator[expr],取系數(shù)的Coefficient[expr],因式分解的Factor[expr],以及展開的Expand[expr]和ExpandAll[expr],表達(dá)式化簡的Simplify[expr]等。expr代表一個(gè)任意的表達(dá)式。
. 求極限
Limit[expr,x->x0] x->x0時(shí)函數(shù)的極限
Limit[expr,x->x0,Direction->-1] x->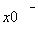 時(shí)函數(shù)的極限
時(shí)函數(shù)的極限
Limit[expr,x->x0, Direction->1] x->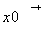 時(shí)函數(shù)的極限
時(shí)函數(shù)的極限
Out[1]:=1
. 微商和微分
在Mathematica中能方便地計(jì)算任何函數(shù)表達(dá)式的任意階微商(導(dǎo)數(shù)).如果f是一元函數(shù),D[f,x]表示 ;如果f是多元函數(shù),D[f,x]表示
;如果f是多元函數(shù),D[f,x]表示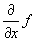 .微商函數(shù)的常用形式如下:
.微商函數(shù)的常用形式如下:
?
?
In[1]:=D[x^x,x]
下面列出全微分函數(shù)Dt的常用形式及其意義:
Dt[f] 全微分
?
Dt[f,x] 全導(dǎo)數(shù)
Dt[f,x1,x2,…] 多重全導(dǎo)數(shù)
In[1]:=Dt[x^2+y^2]
Out[1]:=
?
. 不定積分和定積分
- 不定積分
?
Integreate函數(shù)主要計(jì)算只含有1“簡單函數(shù)”的被積函數(shù). “簡單函數(shù)”包括有理函數(shù)、指數(shù)函數(shù)、對(duì)數(shù)函數(shù)和三角函數(shù)與反三角函數(shù)。不定積分一般形式如下:
Integrate[f,x] 計(jì)算不定積分
Integrate[f,x,y] 計(jì)算不定積分
?
2.定積分
計(jì)算定積分的命令和計(jì)算不定積分是同一個(gè)Integrate函數(shù),在計(jì)算定積分時(shí),除了要給出變量外還要給出積分的上下限。當(dāng)定積分算不出準(zhǔn)確結(jié)果時(shí),用N[%]命令總能得到其數(shù)值解.Nintegrate也是計(jì)算定積分的函數(shù),其使用方法和形式和Integrate函數(shù)相同.用Integrate函數(shù)計(jì)算定積分得到的是準(zhǔn)確解,Nintegrate函數(shù)計(jì)算定積分得到的是近似數(shù)值解.計(jì)算多重積分時(shí),第一個(gè)自變量相應(yīng)于最外層積分放在最后計(jì)算.
Integrate[f,{x,a,b}] 計(jì)算定積分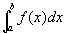
NIntegrate[f,{x,a,b}] 計(jì)算定積分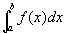
Integrate[f,{x,a,b},{y,c,d}] 計(jì)算定積分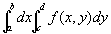
NIntegrate[f,{x,a,b},{y,c,d}] 計(jì)算定積分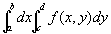
?
?
. 冪級(jí)數(shù)
冪級(jí)數(shù)展開函數(shù)Series的一般形式:
?
Series[expr,{x,x0,n}] 將expr在x=x0點(diǎn)展開到n階的級(jí)數(shù)
Series[expr,{x,x0,n},{y,y0,m}] 先對(duì)y展開到m階再對(duì)x展開n階冪級(jí)數(shù)
用Series展開后,展開項(xiàng)中含有截?cái)嗾`差
?
. 常微分方程
求解常微分方程和常微分方程組的函數(shù)的一般形式如下:
Dsolve[eqns,y[x],x] 解y(x)的微分方程或方程組eqns,x為變量
Dsolve[eqns,y,x] 在純函數(shù)的形式下求解
NDsolve[eqns,y[x],x,{xmin,xmax}] 在區(qū)間{xmin,xmax}上求解變量x的數(shù)的形式下求解常微分方程和常微分方程組eqns的數(shù)值解
Out[3]:= 
.線性代數(shù)
- 定義向量和矩陣函數(shù)
- 矩陣的運(yùn)算符號(hào)和函數(shù)
- 方程組求解函數(shù)
?
定義一個(gè)矩陣,可用函數(shù)Table或Array.當(dāng)矩陣元素能用一個(gè)函數(shù)表達(dá)式時(shí),用函數(shù)Table在定義矩陣大小的同時(shí)也給每個(gè)矩陣元素定義確定的值.用函數(shù)Range只能定義元素為數(shù)值的向量.Array只能用于定義向量、矩陣和張量,并規(guī)定矩陣和張量的元素下標(biāo)從1開始.Array的一般形式: Array[向量元素名,n,f] 定義下標(biāo)從f開始的有n個(gè)元素的向量,當(dāng)f是1時(shí)可省略. Array[矩陣元素名,{m,n}] 定義m行n列的矩陣.其中:矩陣元素名是一個(gè)標(biāo)識(shí)符,表示矩陣元素的名稱,當(dāng)循環(huán)范圍是{u,v,w}時(shí)定義一個(gè)張量. Table[表達(dá)式f,循環(huán)范圍] 表達(dá)式f表示向量或矩陣元素的通項(xiàng)公式;循環(huán)范圍定義矩陣的大小. 循環(huán)范圍的一般形式:{循環(huán)變量名,循環(huán)初值,循環(huán)終值,循環(huán)步長}. 在Array或Table的循環(huán)范圍表示方法略有區(qū)別.請(qǐng)?jiān)谙旅娴膶?shí)例中注意觀察.
Out[1]:= 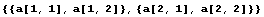 (*矩陣每一行元素用一對(duì){}括起來*)
(*矩陣每一行元素用一對(duì){}括起來*)
In[3]:=  (*IndentityMatrix[n]生成n維矩陣*)
(*IndentityMatrix[n]生成n維矩陣*)
In[4]:= 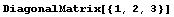 (*生成對(duì)角元素為表元素的對(duì)角矩陣*)
(*生成對(duì)角元素為表元素的對(duì)角矩陣*)
In[5]:= 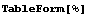 (*TableForm[m]或MatrixForm[m]按矩陣形式輸出m*)
(*TableForm[m]或MatrixForm[m]按矩陣形式輸出m*)
一個(gè)矩陣可用一個(gè)變量表示,如In[2]所示U是一個(gè)矩陣,則U[[I]]表示U的第I行的N個(gè)元素;Transpose[U][[j]]表示U的第J行的M個(gè)元素;U[[I,j]]或a[I,j]表示U的第I行第J列元素;U[[{i1,i2,…,ip},{j1,j2,…,jq}]]表示由行為{i1,i2,…,ip}和列為{j1,j2,…,jq}組成的子矩陣.
?
?
表達(dá)式 |
意義 |
A+c |
A為矩陣,c為標(biāo)量,c與A中的每一個(gè)元素相加 |
A+B |
A,B為同階矩陣或向量,A與B的對(duì)應(yīng)元素相加 |
cA |
A為矩陣,c為標(biāo)量,c與A中的每個(gè)元素相乘 |
U.V |
向量U與V的內(nèi)積 |
A.B |
矩陣A與矩陣B相乘,要求A的列數(shù)等于B的行數(shù) |
Det[M] |
計(jì)算矩陣M的行列式的值 |
Transepose[M] |
|
Inverse[M] |
|
Eigenvalus[A] |
計(jì)算矩陣A的全部(準(zhǔn)確解)特征值 |
Eigenvalus[N[A]] |
計(jì)算矩陣A的全部(數(shù)值解)特征值 |
Eigenvectors[A] |
計(jì)算矩陣A的全部(準(zhǔn)確解)特征向量 |
Eigenvectors[N[A]] |
計(jì)算矩陣A的全部(數(shù)值解)特征向量 |
Eigensystem[A] |
計(jì)算矩陣A的所有(準(zhǔn)確解)特征值和特征向量 |
Eigensystem[N[A]] |
計(jì)算矩陣A的所有(數(shù)值解)特征值和特征向量 |
?
?
在Mathematica中用LinerSolve[A,B],求解滿足AX=B的一個(gè)解.如果A的行列式不為零,那么這個(gè)解是方程組的唯一解; 如果A的行列式是零,那么這個(gè)解是方程組的一個(gè)特解,方程組的全部解由基礎(chǔ)解系向量的線性組合加上這個(gè)特解組成. NullSpace[A]計(jì)算方程組AX=0的基礎(chǔ)解系的向量表,用LinerSolve[A,B]和NullSpace[A]聯(lián)手解出方程組AX=B的全部解. Mathematica中還有一個(gè)美妙的函數(shù)RowReduce[A],它對(duì)A的行向量作化間成梯形的初等線性變換.用RowReduce可計(jì)算矩陣的秩,判斷向量組是線性相關(guān)還是線性無關(guān)和計(jì)算極大線性無關(guān)組等工作.
解方程組函數(shù) |
意義 |
RowReduce[A] |
作行的線性組合化簡A,A為m行n列的矩陣 |
LinerSolve[A,B] |
求解滿足AX=B的一個(gè)解,A為方陣 |
|
NullSpace[A] |
求解方程組AX=0的基礎(chǔ)解系的向量表, A為方陣 |
例:已知A=![]()
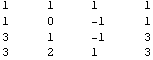 ,計(jì)算A的秩,計(jì)算AX=0的基礎(chǔ)解系.
,計(jì)算A的秩,計(jì)算AX=0的基礎(chǔ)解系.
In[1]:= 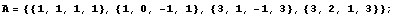 In[2]:=
In[2]:= 
In[3]:= 
Out[3]:= ![]() (*A的兩個(gè)線性無關(guān)解*)
(*A的兩個(gè)線性無關(guān)解*)
五.程序流程控制
?
循環(huán)語句有For[賦初值,循環(huán)條件,增量語句,語句塊]表示如果滿足循環(huán)條件,則執(zhí)行語句塊和增量語句,直到不滿足條件為止,While[test,block]表明如果滿足條件test則反復(fù)執(zhí)行語句塊block,否則跳出循環(huán),Do[block,{i,imin,imax,istep}]與前者功能是相同的。還有Goto[lab], Label[lab]提供了程序中無條件跳轉(zhuǎn),Continue[]和Break[]提供了繼續(xù)循環(huán)或跳出循環(huán)的控制,Catch[語句塊1]和Throw[語句塊2]提供了運(yùn)算中對(duì)異常情況的處理。另外,在程序中書寫注釋可以用一對(duì)"(* *)"括起來,注釋可以嵌套。
?
六.其他
?
1. 使用幫助,Mathematica的幫助文件提供了Mathematica內(nèi)核的基本用法的說明,十分詳細(xì),可以參照學(xué)習(xí)。
2. 你可以使用"? 符號(hào)名"或"??符號(hào)名"來獲得關(guān)于該符號(hào)(函數(shù)名或其他)的粗略或詳細(xì)介紹。符號(hào)名中還可以使用通配符,例如?M*,則系統(tǒng)將給出所有以M開頭的關(guān)鍵詞和函數(shù)名,再如??For將會(huì)得到關(guān)于For語句的格式和用法的詳細(xì)情況。
3. 在Mathematica的編輯界面中輸入語句和函數(shù),確認(rèn)光標(biāo)處于編輯狀態(tài)(不斷閃爍),然后按Insert鍵來對(duì)這一段語句進(jìn)行求值。如果語句有錯(cuò),系統(tǒng)將用紅色字體給出 出錯(cuò)信息,你可以對(duì)已輸入的語句進(jìn)行修改,再運(yùn)行。如果運(yùn)行時(shí)間太長,你可以通過Alt+.(Alt+句號(hào))來中止求值。
4. 對(duì)函數(shù)名不確定的,可先輸入前面幾個(gè)字母(開頭一定要大寫),然后按Ctrl+K,系統(tǒng)會(huì)自動(dòng)補(bǔ)全該函數(shù)名。
?
七.應(yīng)用例子
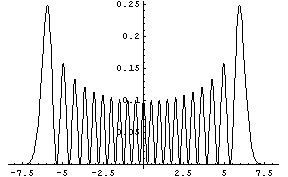
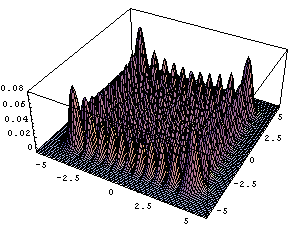
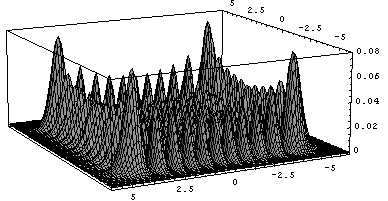
量子一維、二維簡諧振子問題
量子一維簡諧振子圖像
量子二維簡諧振子圖像
 電子發(fā)燒友App
電子發(fā)燒友App







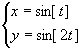

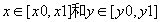
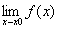
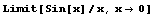


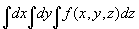
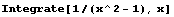
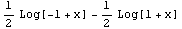
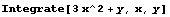
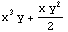
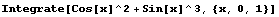
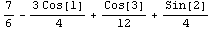
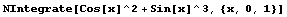
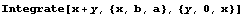
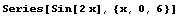
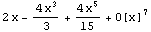

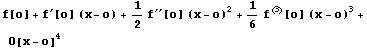
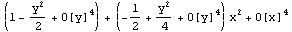
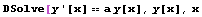
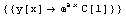
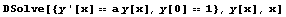
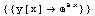
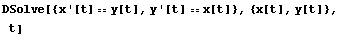
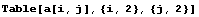
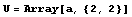



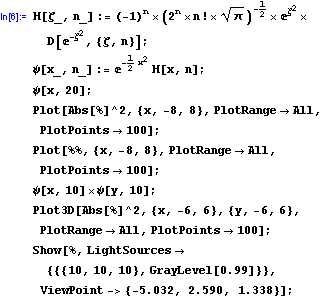
















評(píng)論