Matlab中一些常用的命令

感覺很多確實(shí)還蠻有用的，共享一下！

一、常用對象操作：除了一般windows窗口的常用功能鍵外。

1、！dir 可以查看當(dāng)前工作目錄的文件。 ！dir& 可以在dos狀態(tài)下查看。

2、who 可以查看當(dāng)前工作空間變量名， whos 可以查看變量名細(xì)節(jié)。

3、功能鍵：

功能鍵 快捷鍵 說明

方向上鍵 Ctrl+P 返回前一行輸入

方向下鍵 Ctrl+N 返回下一行輸入

方向左鍵 Ctrl+B 光標(biāo)向后移一個字符

方向右鍵 Ctrl+F 光標(biāo)向前移一個字符

Ctrl+方向右鍵 Ctrl+R 光標(biāo)向右移一個字符

Ctrl+方向左鍵 Ctrl+L 光標(biāo)向左移一個字符

home Ctrl+A 光標(biāo)移到行首

End Ctrl+E 光標(biāo)移到行尾

Esc Ctrl+U 清除一行

Del Ctrl+D 清除光標(biāo)所在的字符

Backspace Ctrl+H 刪除光標(biāo)前一個字符

Ctrl+K 刪除到行尾

Ctrl+C 中斷正在執(zhí)行的命令

4、clc可以命令窗口顯示的內(nèi)容，但并不清除工作空間。

二、函數(shù)及運(yùn)算

1、運(yùn)算符：

＋：加， －：減， *：乘， /： 除， ：左除 ^： 冪，‘：復(fù)數(shù)的共軛轉(zhuǎn)置， （）：制定運(yùn)算順序。

2、常用函數(shù)表：

sin（ ） 正弦（變量為弧度）

Cot（ ） 余切（變量為弧度）

sind（ ） 正弦（變量為度數(shù)）

Cotd（ ） 余切（變量為度數(shù)）

asin（ ） 反正弦（返回弧度）

acot（ ） 反余切（返回弧度）

Asind（ ） 反正弦（返回度數(shù)）

acotd（ ） 反余切（返回度數(shù)）

cos（ ） 余弦（變量為弧度）

exp（ ） 指數(shù)

cosd（ ） 余弦（變量為度數(shù)）

log（ ） 對數(shù)

acos（ ） 余正弦（返回弧度）

log10（ ） 以10為底對數(shù)

acosd（ ） 余正弦（返回度數(shù)）

sqrt（ ） 開方

tan（ ） 正切（變量為弧度）

realsqrt（ ） 返回非負(fù)根

tand（ ） 正切（變量為度數(shù)）

abs（ ） 取絕對值

atan（ ） 反正切（返回弧度）

angle（ ） 返回復(fù)數(shù)的相位角

atand（ ） 反正切（返回度數(shù)）

mod（x，y） 返回x/y的余數(shù)

sum（ ） 向量元素求和

3、其余函數(shù)可以用help elfun和help specfun命令獲得。

4、常用常數(shù)的值：

pi 3.1415926……。

realmin 最小浮點(diǎn)數(shù)，2^-1022

i 虛數(shù)單位

realmax 最大浮點(diǎn)數(shù)，（2－eps）2^1022

j 虛數(shù)單位

Inf 無限值

eps 浮點(diǎn)相對經(jīng)度＝2^-52

NaN 空值

三、數(shù)組和矩陣：

1、構(gòu)造數(shù)組的方法：增量發(fā)和linspace（first，last，num）first和last為起始和終止數(shù)，num為需要的數(shù)組元素個數(shù)。

2、構(gòu)造矩陣的方法：可以直接用［ ］來輸入數(shù)組，也可以用以下提供的函數(shù)來生成矩陣。

ones（ ） 創(chuàng)建一個所有元素都為1的矩陣，其中可以制定維數(shù)，1，2…。個變量

zeros（） 創(chuàng)建一個所有元素都為0的矩陣

eye（） 創(chuàng)建對角元素為1，其他元素為0的矩陣

diag（） 根據(jù)向量創(chuàng)建對角矩陣，即以向量的元素為對角元素

magic（） 創(chuàng)建魔方矩陣

rand（） 創(chuàng)建隨機(jī)矩陣，服從均勻分布

randn（） 創(chuàng)建隨機(jī)矩陣，服從正態(tài)分布

randperm（） 創(chuàng)建隨機(jī)行向量

horcat C=［A，B］，水平聚合矩陣，還可以用cat（1，A，B）

vercat C=［A;B］，垂直聚合矩陣， 還可以用cat（2，A，B）

repmat（M，v，h） 將矩陣M在垂直方向上聚合v次，在水平方向上聚合h次

blkdiag（A，B） 以A，和B為塊創(chuàng)建塊對角矩陣

length 返回矩陣最長維的的長度

ndims 返回維數(shù)

numel 返回矩陣元素個數(shù)

size 返回每一維的長度，［rows，cols］=size（A）

reshape 重塑矩陣，reshape（A，2，6），將A變?yōu)?×6的矩陣，按列排列。

rot90 旋轉(zhuǎn)矩陣90度，逆時(shí)針方向

fliplr 沿垂軸翻轉(zhuǎn)矩陣

flipud 沿水平軸翻轉(zhuǎn)矩陣

transpose 沿主對角線翻轉(zhuǎn)矩陣

ctranspose 轉(zhuǎn)置矩陣，也可用A’或A.’，這僅當(dāng)矩陣為復(fù)數(shù)矩陣時(shí)才有區(qū)別

inv 矩陣的逆

det 矩陣的行列式值

trace 矩陣對角元素的和

norm 矩陣或矢量的范數(shù)，norm（a，1），norm（a，Inf）……。

normest 估計(jì)矩陣的最大范數(shù)矢量

chol 矩陣的cholesky分解

cholinc 不完全cholesky分解

lu LU分解

luinc 不完全LU分解

qr 正交分解

kron（A，B） A為m×n，B為p×q，則生成mp×nq的矩陣，A的每一個元素都會乘上B，并占據(jù)p×q大小的空間

rank 求出矩陣的刺

pinv 求偽逆矩陣

A^p 對A進(jìn)行操作

A.^P 對A中的每一個元素進(jìn)行操作

四、數(shù)值計(jì)算

1、線性方程組求解

（1）AX=B的解可以用X＝AB求。XA=B的解可以用X=A/B求。如果A是m×n的矩陣，當(dāng)m＝n時(shí)可以找到唯一解，m《n，不定解，解中至多有m個非零元素。如果m》n，超定系統(tǒng)，至少找到一組解。如果A是奇異的，且AX=B有解，可以用X＝pinv（A）×B返回最小二乘解

（2）AX=b， A＝L×U，［L，U］=lu（A）， X=U（Lb），即用LU分解求解。

（3）QR（正交）分解是將一矩陣表示為一正交矩陣和一上三角矩陣之積，A＝Q×R［Q，R］=chol（A）， X=Q（Ub）

（4）cholesky分解類似。

2、特征值

D＝eig（A）返回A的所有特征值組成的矩陣。［V，D］=eig（A），還返回特征向量矩陣。

3、A＝U×S×UT，［U，S］=schur（A）。其中S的對角線元素為A的特征值。

4、多項(xiàng)式Matlab里面的多項(xiàng)式是以向量來表示的，其具體操作函數(shù)如下：

conv 多項(xiàng)式的乘法

deconv 多項(xiàng)式的除法，【a，b】＝deconv（s），返回商和余數(shù)

poly 求多項(xiàng)式的系數(shù)（由已知根求多項(xiàng)式的系數(shù)）

polyeig 求多項(xiàng)式的特征值

Polyfit（x，y，n） 多項(xiàng)式的曲線擬合，x，y為被擬合的向量，n為擬合多項(xiàng)式階數(shù)。

polyder 求多項(xiàng)式的一階導(dǎo)數(shù)，polyder（a，b）返回ab的導(dǎo)數(shù)

［a，b］＝polyder（a，b）返回a/b的導(dǎo)數(shù)。

polyint 多項(xiàng)式的積分

polyval 求多項(xiàng)式的值

polyvalm 以矩陣為變量求多項(xiàng)式的值

residue 部分分式展開式

roots 求多項(xiàng)式的根（返回所有根組成的向量）

注：用ploy（A）求出矩陣的特征多項(xiàng)式，然后再求其根，即為矩陣的特征值。

5、插值常用的插值函數(shù)如下：

griddata 數(shù)據(jù)網(wǎng)格化合曲面擬合

Griddata3 三維數(shù)據(jù)網(wǎng)格化合超曲面擬合

interp1 一維插值（yi=interp1（x，y，xi，’method’）Method=nearest/linear/spline/pchip/cubic

Interp2 二維插值zi=interp1（x，y，z，xi，yi’method’），bilinear

Interp3 三維插值

interpft 用快速傅立葉變換進(jìn)行一維插值，help fft。

mkpp 使用分段多項(xiàng)式

spline 三次樣條插值

pchip 分段hermit插值

6、函數(shù)最值的求解

fminbnd（‘f’，x1，x2，optiset（，））求f在x1和x2之間的最小值。Optiset選項(xiàng)可以有‘Display’+‘iter’/’off’/’final’，分別表示顯示計(jì)算過程/不顯示/只顯示最后結(jié)果。fminsearch求多元函數(shù)的最小值。fzero（‘f’，x1）求一元函數(shù)的零點(diǎn)。X1為起始點(diǎn)。同樣可以用上面的選項(xiàng)。

五、圖像繪制：

1、基本繪圖函數(shù)

plot 繪制二維線性圖形和兩個坐標(biāo)軸

plot3 繪制三維線性圖形和兩個坐標(biāo)軸

fplot 在制定區(qū)間繪制某函數(shù)的圖像。fplot（‘f’，區(qū)域，線型，顏色）

loglog 繪制對數(shù)圖形及兩個坐標(biāo)軸（兩個坐標(biāo)都為對數(shù)坐標(biāo)）semilogx 繪制半對數(shù)坐標(biāo)圖形

semilogy 繪制半對數(shù)坐標(biāo)圖形

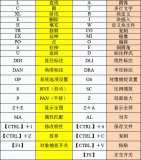
2、線型： 顏色 線型

y 黃色 。 圓點(diǎn)線 v 向下箭頭

g 綠色 -。 組合 》 向右箭頭

b 藍(lán)色 + 點(diǎn)為加號形 《 向左箭頭

m 紅紫色 o 空心圓形 p 五角星形

c 藍(lán)紫色 * 星號 h 六角星形

w 白色 。 實(shí)心小點(diǎn) hold on 添加圖形

r 紅色 x 叉號形狀 grid on 添加網(wǎng)格

k 黑色 s 方形 - 實(shí)線

d 菱形 -- 虛線 ^ 向上箭頭

3、可以用subplot（3，3，1）表示將繪圖區(qū)域分為三行三列，目前使用第一區(qū)域。此時(shí)如要畫不同的圖形在一個窗口里，需要hold on。