FISCO BCOS交易簽名算法基于ECDSA原理進行設計，ECDSA也是比特幣和以太坊采用的交易簽名算法。

本文介紹ECDSA及橢圓曲線加密（ECC）相關知識、ECDSA的Recover機制和實現方式、FISCO BCOS交易簽名和驗簽的底層原理。內容偏硬（shu）核（xue），歡迎對密碼學原理、區塊鏈底層原理感興趣的開發者一起交流。

故事開始

故事要從以太坊中一個神奇的魔數開始說起。

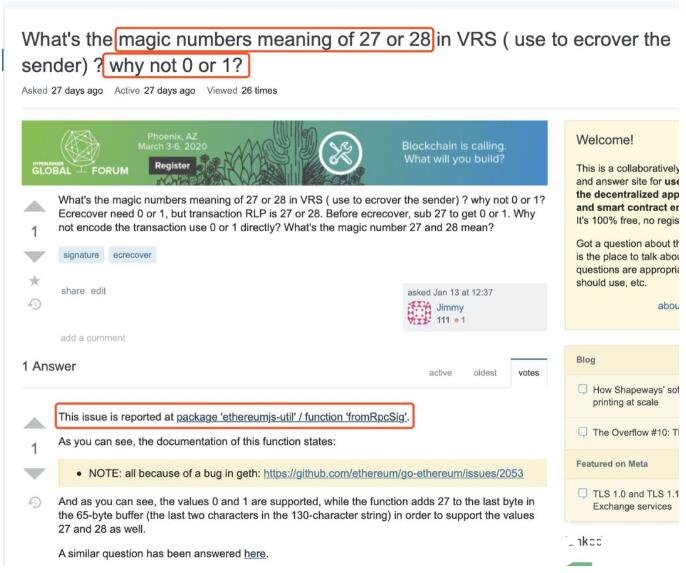
以太坊黃皮書中，關于交易簽名的闡述講到兩個特殊的數「27，28」，實際上是從「0，1」通過加了一個27演變得到「27，28」，所以本質上是一個特殊的數27。

這個特殊的數字27代表了什么含義呢？

一次偵探之旅開始了…

這像是一個bug

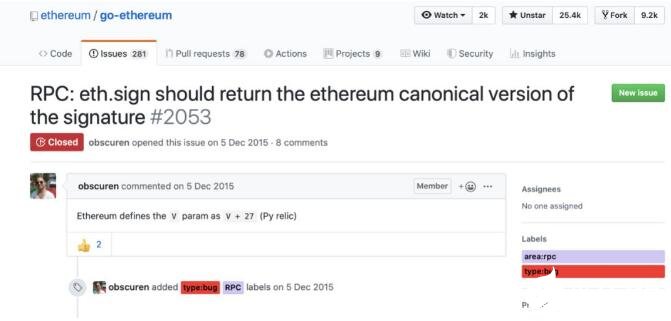
搜索發現此前已有許多關于該問題的討論，其中，Stack Exchange的一篇帖子指出這是一個設計bug。以太坊源碼github上，也有一個相關issue，該issue被打上了「type:bug」的標簽。

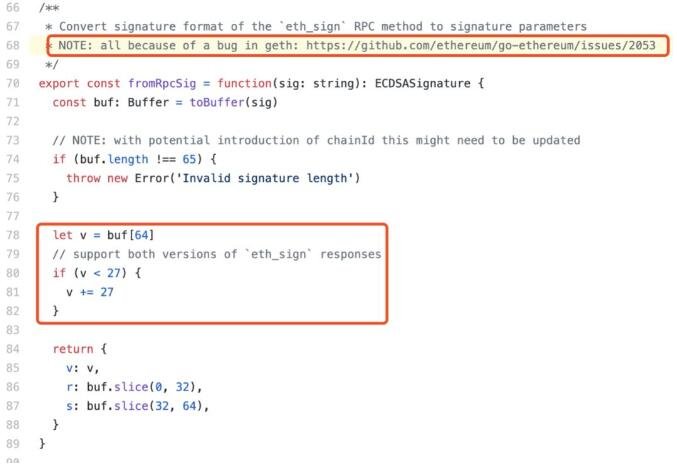
Stack Exchange帖子中有一個鏈接給出了修復該Bug的代碼，請看下面截圖（紅框）。在注釋說明和代碼可見，fromRpcSig函數對27這個魔數進行了特殊處理。從RPC過來的簽名中，v值如果小于27（可能是0-3），則直接加上27作為新v值，fromRpcSig函數通過這個方式兼容ECDSA原始v值（也就是recoveryID）和以太坊v值。

這真是以太坊設計的一個bug嗎？

回到剛才那個fromRpcSig的源代碼文件，詳細看其各接口實現，我們發現有這樣一行代碼「v: chainId ? recovery + (chainId * 2 + 35) : recovery + 27」，這行為v賦值的代碼透露了三個信息，分別是魔數27、魔數35和ChainID。

于是，疑問更多了，魔數35是什么？ChainID又是什么？

這不像是一個Bug

帶著這些疑問，再一次查閱相關設計材料，我們看到，以太坊EIP155中描述了有關ChainID的設計。基于以太坊源碼構建的網絡，實際運行的鏈有很多，為了防止一條鏈的交易被提交上鏈到另一條鏈，造成重放攻擊，引入了ChainID的設計，在塊高2,675,000的位置進行分叉實現。

明白了ChainID的作用，另一個疑問又產生了——以太坊中，有NetworkID來區分不同網絡，為什么還需要ChainID？

這要從NetworkID和ChainID的作用范圍來解釋。NetworkID主要在網絡層面進行鏈的隔離，節點在建立相互連接的時候需要交換NetworkID，擁有一致的NetworkID才能完成握手連接。ChainID是交易層面，防止不同網絡的交易被交叉重復攻擊。

以太坊（ETH）和經典以太坊（ETC）的主網NetworkID都是1，需要通過 ChainID機制才能防止交易在ETH和ETC網絡之間交叉重放，ETH主網的ChainID是1，ETC主網的ChainID是61。

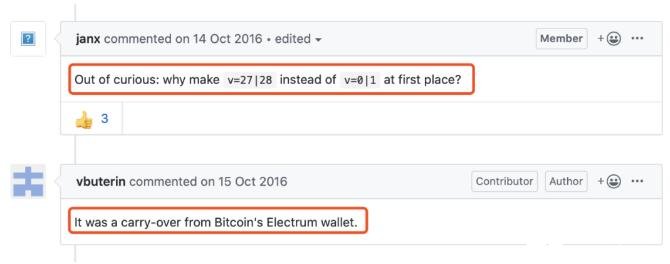
說到這里其實還是沒有搞清楚為什么是27，為什么是35？我們在EIP github的Issue#155中看到Jan和Buterin的交流記錄，看來27是來自比特幣的產物。

順藤摸瓜，打開electrum的github，我們在electrum/electrum/ecc.py中找到如下代碼

從代碼中可見，electrum在簽名時，為原本只有0-3之間的recid（recoveryID）

加上了27，還有一個壓縮標記，如果有壓縮則再加上4，recid的值范圍在27-34。

至此可知，27和35大概來源于此，以太坊繼承比特幣的設計，在比特幣源碼bitcoin/src/key.cpp的CKey::SignCompact函數中也確定了該實現方式，但是比特幣為什么如此設計，仍未可知。

ECDSA才是“bug”

故事到這里，我們對以太坊代碼中那個魔數27的前世今生有大概了解，但這僅僅是故事的開端，由此引發我們進一步思考一個問題：recoveryID是什么？

為了解釋清楚這個問題，我們需要從ECDSA算法著手，從數學角度理解其背后的原理。ECDSA是FISCO BCOS采用的交易簽名算法，由此我們會發現，ECDSA算法有一種Recover機制，它才是真正“bug”級別的功能。

ECDSA（Elliptic Curve Digital Signature Algorithm）是基于橢圓曲線的數字簽名算法。數字簽名算法是采用公私鑰體系實現類似寫在紙上的普通簽名，用于鑒別數字信息的方法，常見的數字簽名算法包括DSA、RSA和ECDSA等。

橢圓曲線密碼（ECC）是基于橢圓曲線數學的公鑰加密算法，建立在橢圓曲線離散對數困難問題之上，常用的協議有ECDH、ECDSA和ECIES等。

橢圓曲線的參數可以有多種配置方式，也就存在多種不同的曲線，例如secp256k1、secp256r1、Curve25519等，不同曲線的安全性存在一些區別，在SafeCurves中有相關對比描述。

ECDSA算法主要包括以下四個關鍵功能：

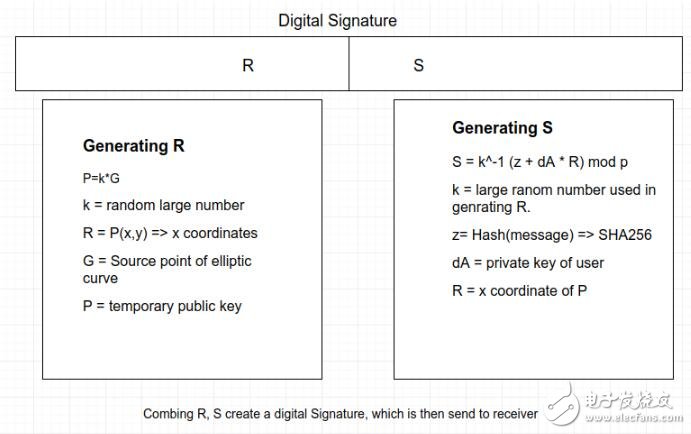
產生密鑰GenKey

· 選擇一條橢圓曲線E_P(a,b)，選擇基點G，G的階數為n

· 選擇隨機數d ∈n為私鑰，計算公鑰Q = d?G

簽名算法Sign

· 對消息m使用消息摘要算法，得到z=hash(m)

· 生成隨機數k∈n，計算點(x, y)=k?G

· 取r=x mod n，若r=0則重新選擇隨機數k

· 計算s = k^?1(z+rd) mod n，若s=0則重新選擇隨機數k

· 上述(r,s)即為ECDSA簽名

驗證算法Verify

使用公鑰Q和消息m，對簽名(r,s)進行驗證。

· 驗證r,s∈n

· 計算z = hash(m)

· 計算u_1 =zs^?1 mod n和u_2 = rs^?1 mod n

· 計算(x, y) = u1?G+u2?Q mod n

· 判斷r == x，若相等則簽名驗證成功

恢復算法Recover

已知消息m和簽名(r,s)，恢復計算出公鑰Q。

· 驗證r, s∈n

· 計算R=(x, y)，其中x=r,r+n,r+2n...，代入橢圓曲線方程計算獲得R

· 計算z = hash(m)

· 計算u_1 = ?zr^?1 mod n和u_2 = sr^?1 mod n

· 計算公鑰Q= (x’, y’)=u_1?G+u_2?R

為了回答recoveryID的問題，我們重點關注「恢復算法Recover」。

在計算R的步驟可以看到，存在多個x的取值可能性，導致存在多個R的可能性，因此計算得到的Q也存在多個可能的結果，需要通過和已知的公鑰對比，確定哪一個Q是正確的。如果遍歷x的所有可能都未找到正確的Q，說明該消息和簽名是不對應的，或者是一個未知的公鑰。

為了確定正確的Q，需要遍歷x的所有可能取值，跑多輪Recover算法，這個時間開銷是比較大的。為了提高Recover的時間效率，采用空間換時間的思路，在簽名中增加一個v值，用于快速確定x，避免遍歷查找試探，這個v值就是recoveryID。

在區塊鏈系統中，客戶端對每筆交易進行簽名，節點對交易簽名進行驗證。

如果采用「驗證算法Verify」，那節點必須首先知道簽發該交易所對應的公鑰，因此需要在每筆交易中攜帶公鑰，這需要消耗很大帶寬和存儲。

如果采用「恢復算法Recover」，并且在生成的簽名中攜帶recoveryID，就可以快速恢復出簽發該交易對應的公鑰，根據公鑰計算出用戶地址，然后在用戶地址空間執行相應操作。

這里潛藏了一個區塊鏈設計哲學，區塊鏈上的資源（資產、合約）都是歸屬某個用戶的，如果能夠構造出符合該用戶地址的簽名，等同于掌握了該用戶的私鑰，因此節點無需事先確定用戶公鑰，僅從簽名恢復出公鑰，進而計算出用戶地址，就可以執行這個用戶地址空間的相應操作。

FISCO BCOS基于這個原理設計實現了交易簽名和驗簽。

recoveryID的計算

關于JavaSDK性能優化的文章（記一次JavaSDK性能從8000提升至30000的過程）中提到一個關鍵優化點——recoveryID的計算，這里仔細展開討論。

ECDSA簽名（r,s），其中r是橢圓曲線上一個點kG (x, y)對應的x mod n，相當于簽名信息中只留下了X軸坐標相關的值，丟棄了Y軸相關的值。在「恢復算法Recover」中嘗試找回Y軸對應的值構造R，進而恢復出公鑰。

由于r = x mod n，因此r,r+n,r+2n…都可能是合法的原始x值，不同的橢圓曲線存在不同數量這樣合法的x值，FISCO BCOS采用的secp256k1曲線存在兩個可能r, r+n。

每一個X軸坐標對應兩個可能的Y坐標，因此FISCO BCOS中具備四種可能的R，(r, y) (r, -y) (r+n, y’) (r+n, -y’)。但是，對于一個r值存在兩個X軸坐標的概率極低，低到幾乎可以忽略，以太坊中就忽略了這兩種小概率事件。

那這個小概率事件的概率具體有多小呢？這要從secp256k1曲線的參數說起，通常描述一個橢圓曲線的點（x,y）的時候，x和y的值是 mod p 的結果，p是曲線的參數，它是一個大素數，之前提到的n也是曲線的參數，等于這條曲線上點的數量（曲線上點的數量為n*h，h也是曲線參數，該曲線h=1），在secp256k1中，n和p的值非常接近，具體可見下圖。

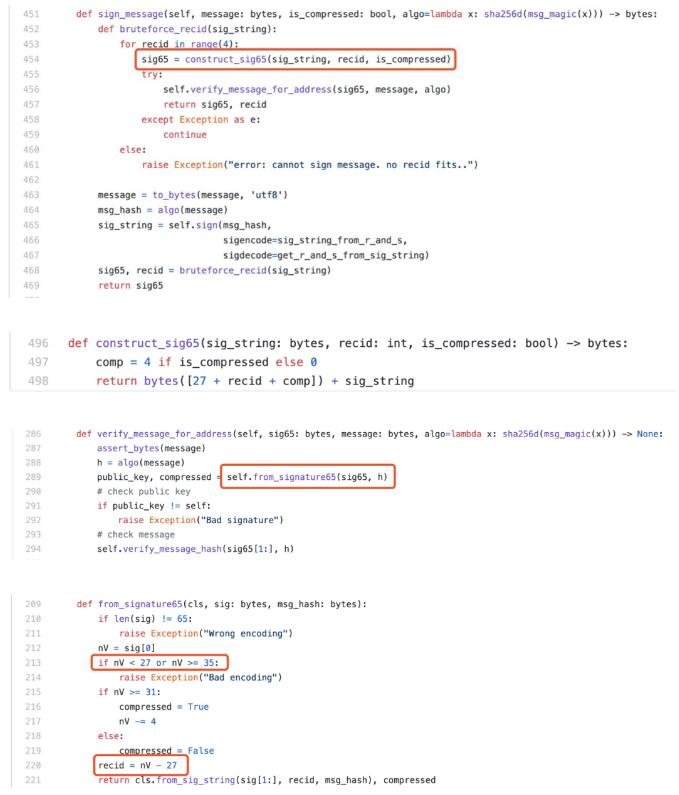
由于r = x mod n，x是mod p的結果，r是mod n的結果，x值的范圍是[0, p-1]，r值的范圍是[0, n-1]。如果r+n也是曲線上的點，則r的值必須小于p-n，概率為 (p-n) / p，大約為3.73*10^-39，這個概率是非常小的。

基于簽名結果（r, s）和簽名過程中生成的隨機點（x, y）的y值，recoveryID的計算方式如下：

1. id = y & 1; //「簽名算法Sign」中kG點的y坐標，根據奇偶性設置id值，因為y是mod p的結果，其奇偶性與坐標軸的正負性是完全對應的

2. id |= (x != r ? 2 : 0); // 小概率事件，如前文解釋

3. if (s > n / 2) id = id ^ 1; // 簽名計算得出的s如果大于n/2就會取n-s作為s值，因此這里做相應轉換，這兩個轉換是同時發生的

JavaSDK性能優化的文章就是基于這個計算公式，將遍歷探尋recoveryID改為計算獲得，大幅提升了性能。

后話

從一個神奇的數字開始，查閱相關資料，了解設計原理，進而闖入ECDSA的世界，在一堆數學公式中迷茫、游蕩，問題一個接著一個。一開始霧里看花，似懂非懂，靠著處女座的潔癖精神，總算把心中疑問一一化解。

精妙絕倫的密碼協議，高深莫測的數學理論，做一個區塊鏈碼農，要學習的東西還很多。唯有苦其心志，勞其筋骨，善待每一個疑點，不放過每一處細節。

總會有一天，那時——撥開云霧見天日，守得云開見月明。
責任編輯；zl