上周三,以太坊創(chuàng)始人Vitalik Buterin在布拉格舉行的Devcon4大會上,公布了以太坊發(fā)展路線(也被稱為以太坊2.0)的最新信息,更新的內(nèi)容包括新鏈將以Serenity為名(之前被稱為Shasper,意指分片和Casper的結(jié)合),其包含了Casper、分片、EWASM以及其他一些協(xié)議,它會是一條新的區(qū)塊鏈,并與當前的以太坊PoW鏈同時存在,且相互連接。
而在第一階段,以太坊開發(fā)者們將交付基礎(chǔ)beacon鏈,第二階段則是推出分片數(shù)據(jù)鏈,第三階段就是啟用狀態(tài)交易(EWASM),最后則是迭代、改進以及添加新技術(shù)。
而在本文當中,我們將探討beacon鏈的Casper共識機制,Casper共識機制其實有兩個大的版本,一個是Casper FFG(Vitalik版),而另一個則是本文要講到的Casper CBC(Vlad版)。
以下內(nèi)容譯自Vitalik最新發(fā)布的帖子《Casper CBC lite via committees》
Casper CBC 的工作流程大致如下:
1.驗證者發(fā)出消息;
2.每則消息指定驗證者正在投票的區(qū)塊,并且還指定了驗證者從其他驗證者處收到的最新消息。
3.驗證者正在投票的區(qū)塊,必須等于或繼承自GHOST分叉選擇規(guī)則的頭部區(qū)塊(使用其他驗證者的最新消息作為輸入)
4.唯一的削減條件是(i)上述規(guī)則,(ii)驗證者不能生成具有相同序列號的兩則消息,(iii)在后面的消息中,驗證者不能引用具有(比早期消息中的驗證者所引用的消息)更早序列號的消息;
5.最終確定性是內(nèi)生的:在某些時候,當有多輪驗證者對X的后代進行投票時,從數(shù)學上講,如果沒有大量驗證者發(fā)出無效消息,頭部就不可能切換到非X塊;而少于這個量的限制,可使用各種啟發(fā)式算法進行檢測和測量。
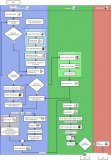
下面是一個GHOST分叉選擇規(guī)則的實例。 字母A,B,C,D,E代表著最近發(fā)生的5次投票。
第一個選擇在綠色和黃色塊之間。最后綠色塊獲勝了,這是因為有三張選票來自綠色塊,而只有兩張選票來自其競爭者黃色塊。第二次選擇是在紅色塊和藍色塊之間。而藍色塊以2:1的比分獲勝,而藍色塊只有一個橙色的子塊,所以橙色塊是獲勝者。
這樣做而導致的效率問題是顯而易見的:每則消息都需要引用它已經(jīng)看到的所有其它消息,這可能會導致O(N^2)的數(shù)據(jù)復雜性;
本文探討了一種緩解數(shù)據(jù)復雜性的特定策略,相較于每個驗證者的投票,都是在每個其他驗證者消息的GHOST分叉選擇規(guī)則進行評估,其中驗證者被明確地分配給m個其他驗證者的私人委員會(可能是32≤m≤256),并且在他們的消息當中,必須包含對這些m個驗證者簽名的引用。
這種引用可以按序列號,或者通過這些簽名已包含在鏈中的位置來完成。削減條件可簡單地檢查這些消息實際上是否代表GHOST分叉選擇評估m(xù)則其他消息,并且計數(shù)器總是遞增的。
更具體地說:
1.對于接受一則消息的鏈,要么 (i) 消息必須對鏈中的區(qū)塊進行投票,要么(ii)該消息投票的鏈外(off-chain)區(qū)塊必須被納入一個叔塊(uncle);
2.對于接受一個叔塊的鏈,這個叔塊的父塊必須 (i)是該鏈的一部分,或者(ii)已經(jīng)被納入了鏈中,并作為一個叔塊;
3.對于一條接受一則消息的鏈,引用其最新集的所有消息,都必須被接受;
4.每則消息都有一個序列號。對于一條接受帶有序列號為n消息的鏈,它必須已接受了來自序列號為0.。..n?1驗證者的消息;
5.驗證者可以對具有相同序列號的兩則消息進行削減處理,或者也可以削減一則投票x的消息,其中消息中包含的證據(jù)不能證明投票x;
如果委員會足夠大,它們將接近整個驗證者集。并且你可以試探性地確定驗證者的數(shù)量。 下面是相關(guān)的代碼:
github.com ethereum/research/blob/659f0b31f9337b3e7ee4bde45cdb93c0ed4fd390/graph_cbc/graph_cbc.py
import random
VALIDATORS = 5000
EDGES = 255
FINALITY = 4000
assert EDGES % 2 == 1
neighbors = list(range(VALIDATORS))
edgelist = neighbors * EDGES
random.shuffle(edgelist)
edges = [edgelist[i*EDGES:i*EDGES+EDGES] for i in range(VALIDATORS)]
last_votes = ‘1’ * FINALITY + ‘0’ * (VALIDATORS - FINALITY)
while 1:
new_zeroes = []
for i in range(VALIDATORS):
votes_for_0 = len([e for e in edges[i] if last_votes[e] == ‘0’])
if votes_for_0 * 2 》 EDGES:
注意,這部分代碼是截取的,完整代碼可訪問:https://github.com/ethereum/research/blob/659f0b31f9337b3e7ee4bde45cdb93c0ed4fd390/graph_cbc/graph_cbc.py
結(jié)果就是m ≈ 256 ,容錯率似乎接近20%,非常接近 Casper CBC兩輪內(nèi)最大的可能值25%。雖然我們失去了幾個百分點的安全性,但我們獲得了一個令人驚訝的簡約協(xié)議表示,否則的話,就可能需要一些相當復雜的數(shù)據(jù)結(jié)構(gòu)。
此外,請注意,這種Casper CBC的風格,基本上與Avalanche(雪崩協(xié)議)的工作方式非常相似,其中每個節(jié)點通過對其他節(jié)點委員會進行調(diào)查而獲得共識。這里的主要區(qū)別在于,委員會是通過協(xié)議選擇的,削減條件會強制執(zhí)行合規(guī)性,而GHOST則被用作分叉選擇規(guī)則,以擴展N元共識鏈,從而有效地實現(xiàn)經(jīng)濟安全。這表明可能存在著一個更為通用的框架,它可以有效地包含Casper CBC以及Avalanche;
進一步的工作:
1.Casper CBC的容錯性,可通過增加的等待回合數(shù),來提高到 (1/3-?)。那么我們是否可以用一種類似的技術(shù),將容錯率提高到20%以上呢?
2.有沒有辦法,在這個設(shè)置當中讓分片自然地發(fā)生呢?一般而言,這種目標,可用某種DAG技術(shù)來替換鏈式機構(gòu)來完成,其中每個區(qū)塊都知道其分片的父級,以及其他分片中的的第十個最新和較舊的區(qū)塊,并且期望驗證者,僅完全驗證尚未被足夠大的驗證者樣本所驗證的區(qū)塊。
 電子發(fā)燒友App
電子發(fā)燒友App



























評論