前言：RSA累加器通過以太坊創(chuàng)始人Vitalik的計算，使用RSA累加器后，原本每年2.5 GB的Plasma子鏈數(shù)據(jù)，可以被壓縮到3.6 MB，壓縮率達到了驚人的99.856%。

然而，這種技術(shù)在其最初的設(shè)計當中，需要用到可信設(shè)置，而來自斯坦福大學(xué)的應(yīng)用密碼學(xué)小組則發(fā)布了一篇題為《用于IOP和無狀態(tài)區(qū)塊鏈的累加器批處理技術(shù)》的論文，論述了一種通過類組（ class group）而無需可信設(shè)置的累加器方法，這些累加器可用于創(chuàng)建無狀態(tài)區(qū)塊鏈（指節(jié)點不需要存儲整個狀態(tài)，以確信哪些區(qū)塊是有效的），以及用于實現(xiàn)高效的UTXO commitment。

在這篇文章中，以太坊區(qū)塊鏈可擴展性和安全研究員Georgios Konstantopoulos對該論文進行了審查，并進行了相關(guān)總結(jié)，以下為譯文：

在這篇文章中，我們將嘗試深入探索RSA累加器，同時回顧一下斯坦福大學(xué)應(yīng)用密碼學(xué)小組最近發(fā)表的論文，這篇非常重要的論文由Benedikt Bunz，Ben Fisch和Dan Boneh共同撰寫，其題目為《用于IOP和無狀態(tài)區(qū)塊鏈的累加器批處理技術(shù)》。

強烈建議大家復(fù)習(xí)下數(shù)學(xué)，以便更好地理解這一技術(shù)。

背景

自1994年以來，累加器便成為了學(xué)術(shù)界非常關(guān)注的一個話題。其類似于默克爾樹（Merkle Tree），并被用于以密碼方式承諾一組數(shù)據(jù)的知識。稍后，可通過發(fā)布證明來證明數(shù)據(jù)集中子集的成員身份。在默克爾樹（Merkle Tree）結(jié)構(gòu)中，證明被稱為默克爾分支（或默克爾證明），并且承諾數(shù)據(jù)的大小是以對數(shù)形式增長的。

另一方面，累加器允許以恒定的大小證明成員身份，以及為多個元素批處理證明（默克爾樹沒有這一特性）。

本文的重點是描述RSA累加器構(gòu)建區(qū)塊、如何構(gòu)建成員和非成員身份的證明，以及如何跨多個區(qū)塊對它們進行批處理。這種特殊的技術(shù)，也在基于UTXO的Plasma中具有應(yīng)用，并由此產(chǎn)生了Plasma原代變異體。設(shè)計一個允許在Plasma中壓縮UTXO集的累加器，需要付出大量的努力。

免責聲明：為了簡單起見，作者模糊處理了這篇文章中的注釋（例如不包括G$中的$U、W\或模塊化算術(shù)的mod N）。

術(shù)語表（來自［1］的定義）：

累加器：“一個密碼學(xué)累加器，其會產(chǎn)生對一組元素的短期約束承諾，以及對集合中任何元素的短期成員身份和非成員身份證明。”

動態(tài)累加器：“支持添加和刪除具有O（1） 成本的元素累加器，其與累積元素數(shù)量無關(guān)。”

通用累加器：“支持成員和非成員身份證明的動態(tài)累加器。”

批處理：批驗證n個證明，要比驗證單個證明要快n倍。

聚合：在一個常量大小的證明中聚合n個成員證明。

未知順序組：組的順序是其集合中元素的數(shù)目。為了保證所提供的證明的安全性，需要生成一組未知順序（否則累加器中使用的模數(shù)有已知的因子分解，并且可以創(chuàng)建偽證明）。生成它可通過多方計算完成，但如果生成方串通檢索生成的數(shù)的階乘，則這是不安全的。它可通過使用類組在沒有可信設(shè)置的情況下生成（注：這點是非常重要的）。

隱序組的簡潔證明

Wesolowski在［2］中提出了指數(shù)方案的知識證明，證明者試圖說服驗證者他們知道一個數(shù)字x，這樣，在已知基數(shù)u下，使得u^x=w成立。

讓我們舉個例子，以2為基數(shù)（u=2），w=16，則得出x=4。我們怎么做？我們把X發(fā)送給驗證者，它們必須執(zhí)行2^4，并對照W檢查結(jié)果。如果匹配，它們便會相信。以下兩個步驟似乎很明顯：

驗證者必須執(zhí)行u^x ：對于大數(shù)字來說，這是一個代價高昂的操作；

將x傳輸?shù)津炞C者：x可能很大，因此傳輸它所需的帶寬可能不小；

讓我們看看有什么協(xié)議可以解決這一挑戰(zhàn)。這些協(xié)議都是交互式的，這意味著驗證者和證明者互相發(fā)送“挑戰(zhàn)”（challenge），這些挑戰(zhàn)在協(xié)議的后續(xù)步驟中會被使用，以確保協(xié)議的安全。

求冪證明（PoE，第3.1節(jié)）

首先，讓我們看看如何讓驗證者信服，而不需要它們實際運行整個求冪運算。

求冪證明（注：當前版本的論文中有一個小錯誤，在第8頁中，作者設(shè)置q=g^q而不是u^q。

“只有當驗證者能夠比計算u^x更快地計算余數(shù)r時，該協(xié)議才有用。它解決了求冪問題，但仍然要求證明者向驗證者傳輸一個潛在的大x，或者x是公開的。”

離散對數(shù)知識證明（PoKE， 第3.3節(jié)）

相比傳輸x，我們可傳輸r。證明變?yōu)椋≦，r），而驗證者必須另外檢查r是否小于l（PoKE*協(xié)議）。當對手可自由地選擇基數(shù)u時，這會是不安全的！

驗證者被證明者愚弄了，他們知道z： u^z=w，而不知道z！

這里破解協(xié)議的細節(jié)在于，證明者選擇了基數(shù)u=g^x，因此x與l是互質(zhì)（co-prime）的。

我們可確定，上述協(xié)議適用于在公共參考字符串（CRS）中編碼和固定的基數(shù)g，簡單來說，各方事先就基數(shù)g達成一致，并且不能被對手任意選擇。

該協(xié)議可通過以下方式進行修復(fù)：

對于固定的g，證明z=g^x離散對數(shù)x的知識；

證明同一x也是基為u，w的離散對數(shù)；

所以最后的協(xié)議（PoKE）是：

證明現(xiàn)在是2組元素Q和Q’。 我們能做得更好嗎？

將證明減少到一個組元素，這可通過添加其它交互步驟來完成：

驗證者需要發(fā)送一個額外的挑戰(zhàn)\alpha，以便證明者無法創(chuàng)建假證明。

從交互式證明，到非交互式證明

在隨機Oracle模型中，通過使用Fiat-Shamir heuristic，任何交互式協(xié)議都可變成非交互式的（假設(shè)我們有一個安全的隨機性生成器，例如一個安全的加密哈希函數(shù)）。

PoKE2需要兩個交互步驟，一個是由驗證者挑選給證明者的生成器g，一個是發(fā)送挑戰(zhàn)值l和a。相反，我們可以哈希當前的“抄本”（transcript），并使用輸出作為這些值。因為我們是在隨機的Oracle模型中操作的，所以如果這些值是由驗證者挑選的（以防證明者作弊，或者它們來自哈希函數(shù)）則沒有什么區(qū)別，因為這兩者在統(tǒng)計上是不可區(qū)分的！

每一方生成挑戰(zhàn)參數(shù)，而不需要交互，每次使用哈希函數(shù)和協(xié)議的當前抄本

上述技術(shù)涉及證明函數(shù)w=f（x）=u^x（標量值）的原像（preimage）知識。

這些技術(shù)也可以擴展到支持同態(tài)原像知識的證明，即證明長度n向量x的知識，使得φ（x）=w。

它們也可以在零知識下執(zhí)行。對于已知g，PoKE需要發(fā)送g^x。在驗證協(xié)議的正確性時，我們假設(shè)存在一個模擬器，該模擬器能夠通過了解驗證內(nèi)容x來模擬g^x。這會泄漏信息，因此不是零知識的！論文作者所使用的技術(shù)包括屏蔽輸入，這些輸入通過使用一種類似Schnorr的協(xié)議和佩德森承諾（Pedersen Commitments）技術(shù)來得到證明。如果你并不熟悉這些術(shù)語，可先訪問一下這些內(nèi)容。

RSA累加器

我們在術(shù)語表中給出了累加器的定義。現(xiàn)在，我們將討論支持批量成員證明和非成員證明的通用累加器的構(gòu)造。

構(gòu)造累加器需要從一組未知順序中選擇一個模數(shù)N，該模數(shù)N可以從RSA組中選擇（例如，如果你信任RSA實驗室，則為RSA-2048），也可以通過可信設(shè)置生成。

RSA累加器的初始狀態(tài)，是從未知順序g組中采樣的生成器，這意味著累加器中的元素列表為空［］。

如［3］所述，累加器必須具有準交換數(shù)學(xué)性質(zhì)。

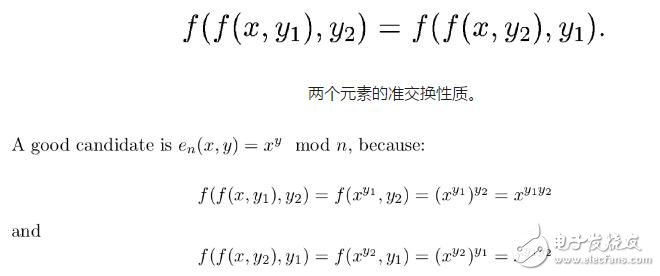
將元素x添加到累加器a，是通過將累加器提升到元素A’ = A^x mod N 來完成的。（為了簡單起見，此處我們省略mod N）

證明成員身份

證明累加器中某個元素的成員身份，需要顯示該元素的值和驗證因子。

驗證因子或共同因子是累加器中所有值的乘積（除了我們正證明的包含值）

（值，驗證因子）對是包含在集合中的證明。

“如果這個值是一個很大的數(shù)字，將其傳遞給驗證者，并且求冪的成本是不可忽略的呢？”

這就是上面的NI-PoKE2協(xié)議的由來。相比發(fā)送上述所述的證明，我們可以證明驗證因子的知識，其會提供一個有效的證明！這似乎不太可能，因為我們的示例很簡單，但我們將在下面的批處理成員證明部分中，看到可能發(fā)生的情況。

證明非成員身份

非成員證明需要計算我們證明的元素的Bezout系數(shù)和集合中元素的乘積。在這里，我們可以找到關(guān)于這個主題的優(yōu)秀指南。

“Vitalik Buterin還提出了一種證明非成員身份的方法，其中他提到的想法是不確定的。（沒有提供其安全性的證明，因此如果你要使用它，可能要小心了！）”

哈希素數(shù)

奇質(zhì)數(shù)（即不帶2的素數(shù)）既需要用于知識證明協(xié)議，也需要用于累加器元素。如果累積的元素不是素數(shù)，那么對手可在元素不在集合中的情況下，愚弄驗證者包含了該元素。

因此，我們必須將累積元素限制為素數(shù)，否則對手可以證明包含累積元素的任何因子（在這種情況下，證明包含3是因為它是6的因子）。

此外，如果NI-PoKE2中的挑戰(zhàn)值l不是素數(shù)，那么我們會得到另一種協(xié)同因子攻擊，其中攻擊者可以計算q，r，從而愚弄驗證者包含了某個元素，這類似于 PoKE*攻擊。

聚合和批處理證明

回憶一下定義：

聚合：將多個證明組合在一個常量大小的證明中；

批處理：一次性驗證多個證明，而不是單次地驗證所有的證明；

聚合和批處理成員證明是是非常簡單的，只需將被證明的值相乘，并為它們提供一個共同因素：

我們可以很快看出，如果我們想要為很多元素創(chuàng)建成員身份的聚合證明，那么值在傳輸時會變大，并且驗證者需要執(zhí)行昂貴的指數(shù)運算。為此，我們使用NI-PoKE2來證明我們知道因子g^65，而不需要向驗證者發(fā)送231，驗證者也不需要進行昂貴的指數(shù)計算（我們實現(xiàn)了批量驗證！）

批處理非成員證明，是通過計算元素 （a’， b’）積的Bezout系數(shù)來完成的，然后具有與以前相同的證明（g^a’，b’）。合并驗證因子的大小，與提供兩個獨立的驗證因子大致相同。

這可以通過將證明設(shè)置為（g^a’， A^b’） 來解決。為了確保安全，證明者還必須提供一個NI-PoKE2，以證明對b‘的了解。

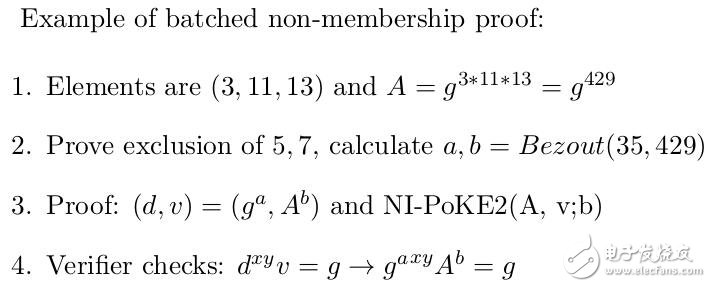
第3步的NI-PoKE2是為了安全考慮，否則對手可能會設(shè)置v = g * d^（-xy），并在不知道b的情況下愚弄驗證者。

這可以通過應(yīng)用NI-PoE來提高效率，這樣驗證者就不需要在最后一步執(zhí)行求冪運算。

在一個恒定大小驗證因子的情況下，目前并沒有有效的算法來聚合非成員證明。

移除可信設(shè)置

所有的指數(shù)運算都關(guān)于模N，這是一個具有未知素數(shù)因子分解的數(shù)字。這是因為提供的所有證明，都在未知順序組的通用組模型中（第2頁），并且需要強RSA假設(shè)和自適應(yīng)根假設(shè)。

在不知道相關(guān)私鑰的情況下生成公鑰是困難的。如論文第2頁中的［2］所述，我們可通過執(zhí)行安全的多方計算來創(chuàng)建所需的數(shù)字，但必須相信參與受信任設(shè)置的各方?jīng)]有串通來找回秘密。Wesolowski在［2］中通過所謂的“類組”（class groups）而提出了另一種選擇：

“一個更好的方法是使用虛二次序（imaginary quadratic order）的類組。事實上，通過選擇一個隨機的判別式，我們可以很容易地生成一個虛二次序，當判別式足夠大時，就無法計算類組的順序。”

目前，Chia正在為有效計算這種“類組”而進行競爭，同時還提供了一份有關(guān)其背后所需理論的綜合性論文。

結(jié)論

如果你能看到這里，那么祝賀你！

我們簡要介紹了RSA累加器的工作原理，以及如何構(gòu)造有效證明累加器中元素的成員身份和非成員身份的方案。原論文作者還提供了構(gòu)造向量承諾的方法，其在不同的索引處有成批的opening，這不是默克爾樹的特征。作者構(gòu)建了第一個能夠?qū)崿F(xiàn)O（1）opening的向量承諾方案（這里的opening指證明在承諾中某一指標上某一要素的價值）。

應(yīng)用例子

這些累加器可用于創(chuàng)建無狀態(tài)區(qū)塊鏈（指節(jié)點不需要存儲整個狀態(tài)，以確信哪些區(qū)塊是有效的）。它們還可用于實現(xiàn)高效的UTXO承諾，允許用戶在不知道整個UTXO集的情況下發(fā)布交易。最后，向量承諾可用于創(chuàng)建簡短的交互式Oracle證明，這一過程比使用默克爾樹（Merkle Tree）結(jié)構(gòu)更為有效。

下一步是什么？

這是一篇非常好的論文，它介紹并形式化了很多可用于區(qū)塊鏈結(jié)構(gòu)擴展性的原語。

特別是，RSA累加器已吸引了Plasma研究社區(qū)成員的關(guān)注，他們正設(shè)法利用它來壓縮Plasma Cash的UTXO歷史。最近，ethresear.ch上已經(jīng)有很多關(guān)于如何構(gòu)造它的文章。因此，在下一篇文章中，我們將對當前的方案、它們的優(yōu)缺點以及哪一個方案最為有效進行盤點。

對于可利用向量承諾的非同質(zhì) Plasma 結(jié)構(gòu)，我也非常感興趣。

誰知道呢，也許已經(jīng)有人在做這個了？

關(guān)于這一話題，接下來的文章題目會是： Plasma中的RSA累加器分類。