FM和FFM原理的探索和應用的經驗
大小:0.4 MB 人氣: 2017-10-12 需要積分:1
前言
在計算廣告領域,點擊率CTR(click-through rate)和轉化率CVR(conversion rate)是衡量廣告流量的兩個關鍵指標。準確的估計CTR、CVR對于提高流量的價值,增加廣告收入有重要的指導作用。預估CTR/CVR,業界常用的方法有人工特征工程 + LR(Logistic Regression)、GBDT(Gradient Boosting Decision Tree) + LR[1][2][3]、FM(Factorization Machine)[2][7]和FFM(Field-aware Factorization Machine)[9]模型。在這些模型中,FM和FFM近年來表現突出,分別在由Criteo和Avazu舉辦的CTR預測競賽中奪得冠軍[4][5]。
考慮到FFM模型在CTR預估比賽中的不俗戰績,美團點評技術團隊在搭建DSP(Demand Side Platform)[6]平臺時,在站內CTR/CVR的預估上使用了該模型,取得了不錯的效果。本文是基于對FFM模型的深度調研和使用經驗,從原理、實現和應用幾個方面對FFM進行探討,希望能夠從原理上解釋FFM模型在點擊率預估上取得優秀效果的原因。因為FFM是在FM的基礎上改進得來的,所以我們首先引入FM模型,本文章節組織方式如下:
首先介紹FM的原理。其次介紹FFM對FM的改進。然后介紹FFM的實現細節。最后介紹模型在DSP場景的應用。
FM原理
FM(Factorization Machine)是由Konstanz大學Steffen Rendle(現任職于Google)于2010年最早提出的,旨在解決稀疏數據下的特征組合問題[7]。下面以一個示例引入FM模型。假設一個廣告分類的問題,根據用戶和廣告位相關的特征,預測用戶是否點擊了廣告。源數據如下[8]
Clicked?
Country
Day
Ad_type
1 USA 26/11/15 Movie
0 China 1/7/14 Game
1 China 19/2/15 Game
“Clicked?”是label,Country、Day、Ad_type是特征。由于三種特征都是categorical類型的,需要經過獨熱編碼(One-Hot Encoding)轉換成數值型特征。
Clicked?
Country=USA
Country=China
Day=26/11/15
Day=1/7/14
Day=19/2/15
Ad_type=Movie
Ad_type=Game
1 1 0 1 0 0 1 0
0 0 1 0 1 0 0 1
1 0 1 0 0 1 0 1
由上表可以看出,經過One-Hot編碼之后,大部分樣本數據特征是比較稀疏的。上面的樣例中,每個樣本有7維特征,但平均僅有3維特征具有非零值。實際上,這種情況并不是此例獨有的,在真實應用場景中這種情況普遍存在。例如,CTR/CVR預測時,用戶的性別、職業、教育水平、品類偏好,商品的品類等,經過One-Hot編碼轉換后都會導致樣本數據的稀疏性。特別是商品品類這種類型的特征,如商品的末級品類約有550個,采用One-Hot編碼生成550個數值特征,但每個樣本的這550個特征,有且僅有一個是有效的(非零)。由此可見,數據稀疏性是實際問題中不可避免的挑戰。
One-Hot編碼的另一個特點就是導致特征空間大。例如,商品品類有550維特征,一個categorical特征轉換為550維數值特征,特征空間劇增。
同時通過觀察大量的樣本數據可以發現,某些特征經過關聯之后,與label之間的相關性就會提高。例如,“USA”與“Thanksgiving”、“China”與“Chinese New Year”這樣的關聯特征,對用戶的點擊有著正向的影響。換句話說,來自“China”的用戶很可能會在“Chinese New Year”有大量的瀏覽、購買行為,而在“Thanksgiving”卻不會有特別的消費行為。這種關聯特征與label的正向相關性在實際問題中是普遍存在的,如“化妝品”類商品與“女”性,“球類運動配件”的商品與“男”性,“電影票”的商品與“電影”品類偏好等。因此,引入兩個特征的組合是非常有意義的。
多項式模型是包含特征組合的最直觀的模型。在多項式模型中,特征 xi 和 xj 的組合采用 xixj 表示,即 xi 和 xj 都非零時,組合特征 xixj 才有意義。從對比的角度,本文只討論二階多項式模型。模型的表達式如下:
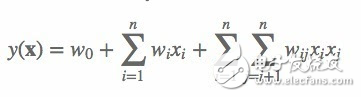
(1)
其中,n 代表樣本的特征數量,xi 是第 i 個特征的值,w0、wi、wij 是模型參數。
從公式(1)可以看出,組合特征的參數一共有 n(n?1)/2 個,任意兩個參數都是獨立的。然而,在數據稀疏性普遍存在的實際應用場景中,二次項參數的訓練是很困難的。其原因是,每個參數 wij 的訓練需要大量 xi 和 xj 都非零的樣本;由于樣本數據本來就比較稀疏,滿足“xi 和 xj 都非零”的樣本將會非常少。訓練樣本的不足,很容易導致參數 wij 不準確,最終將嚴重影響模型的性能。
那么,如何解決二次項參數的訓練問題呢?矩陣分解提供了一種解決思路。在model-based的協同過濾中,一個rating矩陣可以分解為user矩陣和item矩陣,每個user和item都可以采用一個隱向量表示[8]。比如在下圖中的例子中,我們把每個user表示成一個二維向量,同時把每個item表示成一個二維向量,兩個向量的點積就是矩陣中user對item的打分。
非常好我支持^.^
(0) 0%
不好我反對
(0) 0%
