基于水平線搜索算法解矩形件排樣優(yōu)化
大小:1.16 MB 人氣: 2017-10-28 需要積分:1
標簽:水平線搜索(1680)
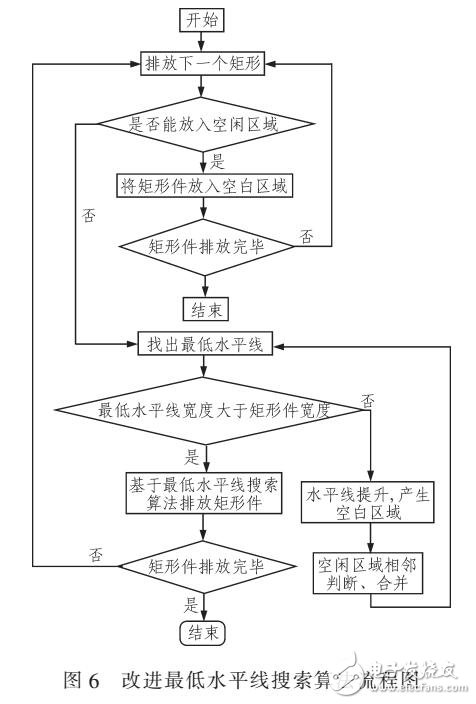
矩形件排樣優(yōu)化的問題是指將不同數(shù)量、大小不一的矩形件按照特定的順序,采取某種排布策略排放到矩形板材上(在本文中,假定矩形板材寬度一定,長度不限),同時滿足特定的約束條件,并且使得板材的利用率能夠最大化2。矩形件排樣優(yōu)化的問題廣泛存在于鈑金下料、造紙工業(yè)、玻璃切割、家具生產(chǎn)等現(xiàn)代制造、加工行業(yè)中。當前社會的發(fā)展對于資源的消耗日益增大,特別對于鋼材等工業(yè)原料的需求越來越大。提高原材料的利用率對于保護生態(tài)環(huán)境,提高企業(yè)的生產(chǎn)率進而獲得更大的經(jīng)濟效益。然而,矩形件排樣優(yōu)化問題屬于NP 完全問題,無法在短時間內(nèi)求得最優(yōu)解。難點主要在于如下兩點:第一矩形件在板材上面進行布局的策略,即排布算法;第二,矩形件的排放順序。目前,通常采用啟發(fā)式算法,例如遺傳算法,模擬退火算法中,蟻群算法,粒子群算法問等,再結(jié)合某種排布規(guī)則,例如BL 算法7,最低水平線算法圖,分層排布算法剛等。文中將分布估計算法與一種改進的最低水平線搜索算法結(jié)合起來求解矩形件排樣優(yōu)化問題。
非常好我支持^.^
(0) 0%
不好我反對
(0) 0%
