閱讀目錄
1. 順序查找
2. 二分查找
3. 插值查找
4. 斐波那契查找
5. 樹表查找
6. 分塊查找
7. 哈希查找
查找是在大量的信息中尋找一個特定的信息元素,在計算機應用中,查找是常用的基本運算,例如編譯程序中符號表的查找。本文簡單概括性的介紹了常見的七種查找算法,說是七種,其實二分查找、插值查找以及斐波那契查找都可以歸為一類——插值查找。插值查找和斐波那契查找是在二分查找的基礎上的優化查找算法。樹表查找和哈希查找會在后續的博文中進行詳細介紹。
查找定義:根據給定的某個值,在查找表中確定一個其關鍵字等于給定值的數據元素(或記錄)。
查找算法分類:
1)靜態查找和動態查找;
注:靜態或者動態都是針對查找表而言的。動態表指查找表中有刪除和插入操作的表。
2)無序查找和有序查找。
無序查找:被查找數列有序無序均可;
有序查找:被查找數列必須為有序數列。
平均查找長度(Average Search Length,ASL):需和指定key進行比較的關鍵字的個數的期望值,稱為查找算法在查找成功時的平均查找長度。
對于含有n個數據元素的查找表,查找成功的平均查找長度為:ASL = Pi*Ci的和。
Pi:查找表中第i個數據元素的概率。
Ci:找到第i個數據元素時已經比較過的次數。
1. 順序查找
說明:順序查找適合于存儲結構為順序存儲或鏈接存儲的線性表。
基本思想:順序查找也稱為線形查找,屬于無序查找算法。從數據結構線形表的一端開始,順序掃描,依次將掃描到的結點關鍵字與給定值k相比較,若相等則表示查找成功;若掃描結束仍沒有找到關鍵字等于k的結點,表示查找失敗。
復雜度分析:
查找成功時的平均查找長度為:(假設每個數據元素的概率相等) ASL = 1/n(1+2+3+…+n) = (n+1)/2 ;
當查找不成功時,需要n+1次比較,時間復雜度為O(n);
所以,順序查找的時間復雜度為O(n)。
C++實現源碼:
//順序查找intSequenceSearch(inta[],intvalue,intn) {inti;for(i=0;i}
2. 二分查找
說明:元素必須是有序的,如果是無序的則要先進行排序操作。
基本思想:也稱為是折半查找,屬于有序查找算法。用給定值k先與中間結點的關鍵字比較,中間結點把線形表分成兩個子表,若相等則查找成功;若不相等,再根據k與該中間結點關鍵字的比較結果確定下一步查找哪個子表,這樣遞歸進行,直到查找到或查找結束發現表中沒有這樣的結點。
復雜度分析:最壞情況下,關鍵詞比較次數為log2(n+1),且期望時間復雜度為O(log2n);
注:折半查找的前提條件是需要有序表順序存儲,對于靜態查找表,一次排序后不再變化,折半查找能得到不錯的效率。但對于需要頻繁執行插入或刪除操作的數據集來說,維護有序的排序會帶來不小的工作量,那就不建議使用。——《大話數據結構》
C++實現源碼://二分查找(折半查找),版本1intBinarySearch1(inta[],intvalue,intn)
{intlow,high,mid; low=0; high=n-1;while(lowvalue) high=mid-1;if(a[mid]value)returnBinarySearch2(a,value,low,mid-1);if(a[mid]}
3. 插值查找
在介紹插值查找之前,首先考慮一個新問題,為什么上述算法一定要是折半,而不是折四分之一或者折更多呢?
打個比方,在英文字典里面查“apple”,你下意識翻開字典是翻前面的書頁還是后面的書頁呢?如果再讓你查“zoo”,你又怎么查?很顯然,這里你絕對不會是從中間開始查起,而是有一定目的的往前或往后翻。
同樣的,比如要在取值范圍1 ~ 10000 之間 100 個元素從小到大均勻分布的數組中查找5, 我們自然會考慮從數組下標較小的開始查找。
經過以上分析,折半查找這種查找方式,不是自適應的(也就是說是傻瓜式的)。二分查找中查找點計算如下:
mid=(low+high)/2, 即mid=low+1/2*(high-low);
通過類比,我們可以將查找的點改進為如下:
mid=low+(key-a[low])/(a[high]-a[low])*(high-low),
也就是將上述的比例參數1/2改進為自適應的,根據關鍵字在整個有序表中所處的位置,讓mid值的變化更靠近關鍵字key,這樣也就間接地減少了比較次數。
基本思想:基于二分查找算法,將查找點的選擇改進為自適應選擇,可以提高查找效率。當然,差值查找也屬于有序查找。
注:對于表長較大,而關鍵字分布又比較均勻的查找表來說,插值查找算法的平均性能比折半查找要好的多。反之,數組中如果分布非常不均勻,那么插值查找未必是很合適的選擇。
復雜度分析:查找成功或者失敗的時間復雜度均為O(log2(log2n))。
C++實現源碼:
//插值查找intInsertionSearch(inta[],intvalue,intlow,inthigh) {intmid=low+(value-a[low])/(a[high]-a[low])*(high-low);if(a[mid]==value)returnmid;if(a[mid]>value)returnInsertionSearch(a,value,low,mid-1);if(a[mid]}
4. 斐波那契查找
在介紹斐波那契查找算法之前,我們先介紹一下很它緊密相連并且大家都熟知的一個概念——黃金分割。
黃金比例又稱黃金分割,是指事物各部分間一定的數學比例關系,即將整體一分為二,較大部分與較小部分之比等于整體與較大部分之比,其比值約為1:0.618或1.618:1。
0.618被公認為最具有審美意義的比例數字,這個數值的作用不僅僅體現在諸如繪畫、雕塑、音樂、建筑等藝術領域,而且在管理、工程設計等方面也有著不可忽視的作用。因此被稱為黃金分割。
大家記不記得斐波那契數列:1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89…….(從第三個數開始,后邊每一個數都是前兩個數的和)。然后我們會發現,隨著斐波那契數列的遞增,前后兩個數的比值會越來越接近0.618,利用這個特性,我們就可以將黃金比例運用到查找技術中。

基本思想:也是二分查找的一種提升算法,通過運用黃金比例的概念在數列中選擇查找點進行查找,提高查找效率。同樣地,斐波那契查找也屬于一種有序查找算法。
相對于折半查找,一般將待比較的key值與第mid=(low+high)/2位置的元素比較,比較結果分三種情況:
1)相等,mid位置的元素即為所求
2)>,low=mid+1;
3)<,high=mid-1。
斐波那契查找與折半查找很相似,他是根據斐波那契序列的特點對有序表進行分割的。他要求開始表中記錄的個數為某個斐波那契數小1,及n=F(k)-1;
開始將k值與第F(k-1)位置的記錄進行比較(及mid=low+F(k-1)-1),比較結果也分為三種
1)相等,mid位置的元素即為所求
2)>,low=mid+1,k-=2;
說明:low=mid+1說明待查找的元素在[mid+1,high]范圍內,k-=2 說明范圍[mid+1,high]內的元素個數為n-(F(k-1))=Fk-1-F(k-1)=Fk-F(k-1)-1=F(k-2)-1個,所以可以遞歸的應用斐波那契查找。
3)<,high=mid-1,k-=1。
說明:low=mid+1說明待查找的元素在[low,mid-1]范圍內,k-=1 說明范圍[low,mid-1]內的元素個數為F(k-1)-1個,所以可以遞歸 的應用斐波那契查找。
復雜度分析:最壞情況下,時間復雜度為O(log2n),且其期望復雜度也為O(log2n)。
C++實現源碼:
//斐波那契查找.cpp#include"stdafx.h"#include#includeusingnamespacestd;constintmax_size=20;//斐波那契數組的長度/*構造一個斐波那契數組*/voidFibonacci(int*F) { F[0]=0; F[1]=1;for(inti=2;iF[k]-1)//計算n位于斐波那契數列的位置 ++k;int*temp;//將數組a擴展到F[k]-1的長度 temp=newint[F[k]-1]; memcpy(temp,a,n*sizeof(int));for(inti=n;itemp[i]=a[n-1]; while(low<=high) {int?mid=low+F[k-1]-1;if(keytemp[mid]) { ?low=mid+1; ?k-=2; }else {?if(mid=n則說明是擴展的數值,返回n-1} } delete?[]?temp;return?-1; }int?main() {int?a[]?=?{0,16,24,35,47,59,62,73,88,99};int?key=100;int?index=FibonacciSearch(a,sizeof(a)/sizeof(int),key); cout<} 5. 樹表查找
5.1 最簡單的樹表查找算法——二叉樹查找算法。
基本思想:二叉查找樹是先對待查找的數據進行生成樹,確保樹的左分支的值小于右分支的值,然后在就行和每個節點的父節點比較大小,查找最適合的范圍。這個算法的查找效率很高,但是如果使用這種查找方法要首先創建樹。
二叉查找樹(BinarySearch Tree,也叫二叉搜索樹,或稱二叉排序樹Binary Sort Tree)或者是一棵空樹,或者是具有下列性質的二叉樹:
1)若任意節點的左子樹不空,則左子樹上所有結點的值均小于它的根結點的值;
2)若任意節點的右子樹不空,則右子樹上所有結點的值均大于它的根結點的值;
3)任意節點的左、右子樹也分別為二叉查找樹。
二叉查找樹性質:對二叉查找樹進行中序遍歷,即可得到有序的數列。
不同形態的二叉查找樹如下圖所示:
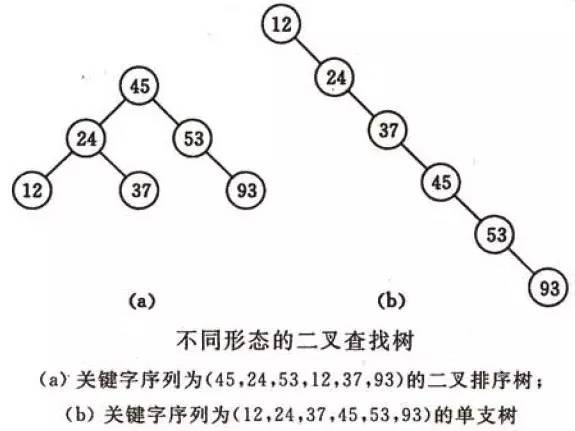
有關二叉查找樹的查找、插入、刪除等操作的詳細講解,請移步淺談算法和數據結構: 七 二叉查找樹。
復雜度分析:它和二分查找一樣,插入和查找的時間復雜度均為O(logn),但是在最壞的情況下仍然會有O(n)的時間復雜度。原因在于插入和刪除元素的時候,樹沒有保持平衡(比如,我們查找上圖(b)中的“93”,我們需要進行n次查找操作)。我們追求的是在最壞的情況下仍然有較好的時間復雜度,這就是平衡查找樹設計的初衷。
下圖為二叉樹查找和順序查找以及二分查找性能的對比圖:
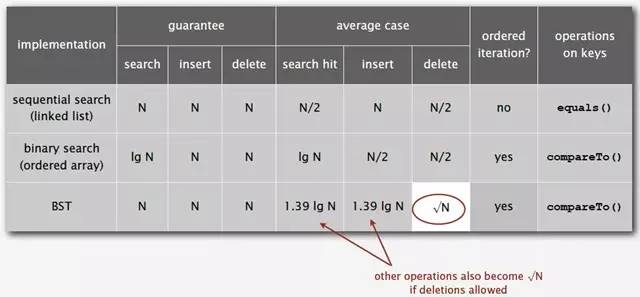
基于二叉查找樹進行優化,進而可以得到其他的樹表查找算法,如平衡樹、紅黑樹等高效算法。
5.2 平衡查找樹之2-3查找樹(2-3 Tree)
2-3查找樹定義:和二叉樹不一樣,2-3樹運行每個節點保存1個或者兩個的值。對于普通的2節點(2-node),他保存1個key和左右兩個自己點。對應3節點(3-node),保存兩個Key,2-3查找樹的定義如下:
1)要么為空,要么:
2)對于2節點,該節點保存一個key及對應value,以及兩個指向左右節點的節點,左節點也是一個2-3節點,所有的值都比key要小,右節點也是一個2-3節點,所有的值比key要大。
3)對于3節點,該節點保存兩個key及對應value,以及三個指向左中右的節點。左節點也是一個2-3節點,所有的值均比兩個key中的最小的key還要小;中間節點也是一個2-3節點,中間節點的key值在兩個跟節點key值之間;右節點也是一個2-3節點,節點的所有key值比兩個key中的最大的key還要大。
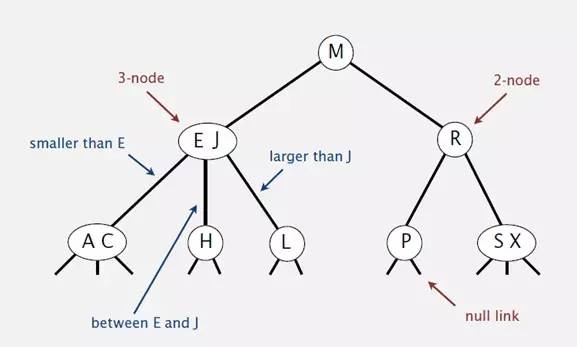
2-3查找樹的性質:
1)如果中序遍歷2-3查找樹,就可以得到排好序的序列;
2)在一個完全平衡的2-3查找樹中,根節點到每一個為空節點的距離都相同。(這也是平衡樹中“平衡”一詞的概念,根節點到葉節點的最長距離對應于查找算法的最壞情況,而平衡樹中根節點到葉節點的距離都一樣,最壞情況也具有對數復雜度。)
性質2)如下圖所示:
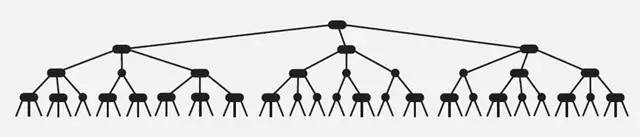
復雜度分析:
2-3樹的查找效率與樹的高度是息息相關的。
在最壞的情況下,也就是所有的節點都是2-node節點,查找效率為lgN
在最好的情況下,所有的節點都是3-node節點,查找效率為log3N約等于0.631lgN
距離來說,對于1百萬個節點的2-3樹,樹的高度為12-20之間,對于10億個節點的2-3樹,樹的高度為18-30之間。
對于插入來說,只需要常數次操作即可完成,因為他只需要修改與該節點關聯的節點即可,不需要檢查其他節點,所以效率和查找類似。下面是2-3查找樹的效率:
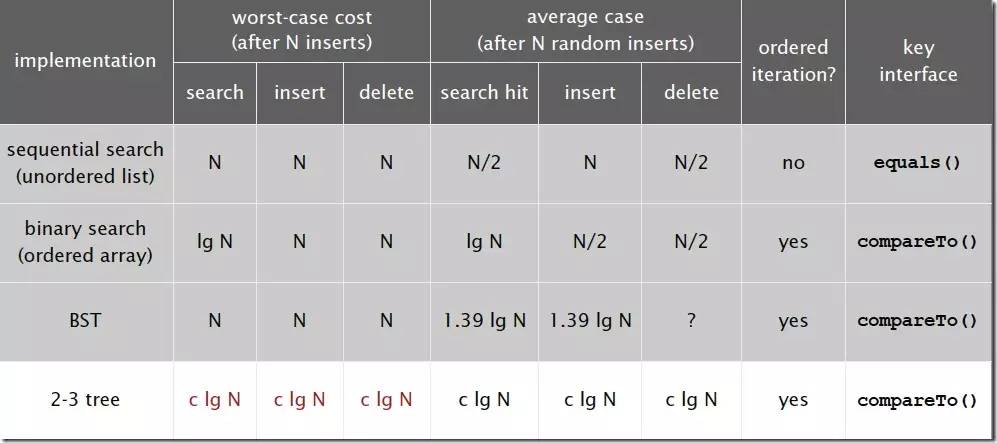
5.3 平衡查找樹之紅黑樹(Red-Black Tree)
2-3查找樹能保證在插入元素之后能保持樹的平衡狀態,最壞情況下即所有的子節點都是2-node,樹的高度為lgn,從而保證了最壞情況下的時間復雜度。但是2-3樹實現起來比較復雜,于是就有了一種簡單實現2-3樹的數據結構,即紅黑樹(Red-Black Tree)。
基本思想:紅黑樹的思想就是對2-3查找樹進行編碼,尤其是對2-3查找樹中的3-nodes節點添加額外的信息。紅黑樹中將節點之間的鏈接分為兩種不同類型,紅色鏈接,他用來鏈接兩個2-nodes節點來表示一個3-nodes節點。黑色鏈接用來鏈接普通的2-3節點。特別的,使用紅色鏈接的兩個2-nodes來表示一個3-nodes節點,并且向左傾斜,即一個2-node是另一個2-node的左子節點。這種做法的好處是查找的時候不用做任何修改,和普通的二叉查找樹相同。
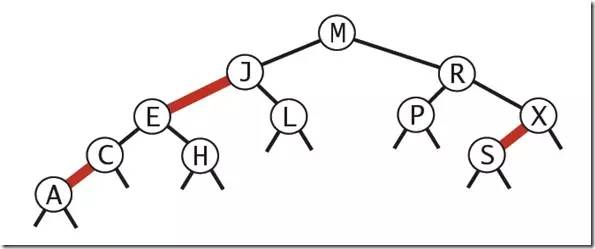
紅黑樹的定義:
紅黑樹是一種具有紅色和黑色鏈接的平衡查找樹,同時滿足:
紅色節點向左傾斜
一個節點不可能有兩個紅色鏈接
整個樹完全黑色平衡,即從根節點到所以葉子結點的路徑上,黑色鏈接的個數都相同。
下圖可以看到紅黑樹其實是2-3樹的另外一種表現形式:如果我們將紅色的連線水平繪制,那么他鏈接的兩個2-node節點就是2-3樹中的一個3-node節點了。
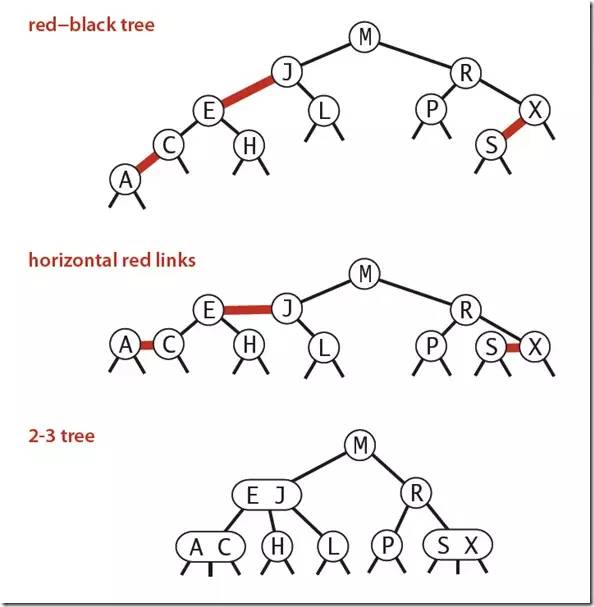
紅黑樹的性質:整個樹完全黑色平衡,即從根節點到所以葉子結點的路徑上,黑色鏈接的個數都相同(2-3樹的第2)性質,從根節點到葉子節點的距離都相等)。
復雜度分析:最壞的情況就是,紅黑樹中除了最左側路徑全部是由3-node節點組成,即紅黑相間的路徑長度是全黑路徑長度的2倍。
下圖是一個典型的紅黑樹,從中可以看到最長的路徑(紅黑相間的路徑)是最短路徑的2倍:
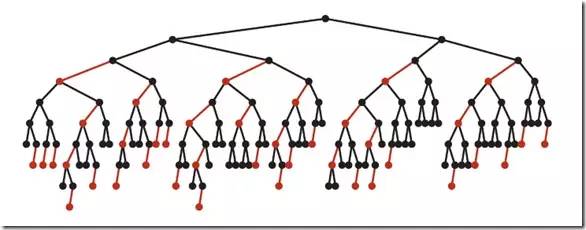
紅黑樹的平均高度大約為logn。
下圖是紅黑樹在各種情況下的時間復雜度,可以看出紅黑樹是2-3查找樹的一種實現,它能保證最壞情況下仍然具有對數的時間復雜度。
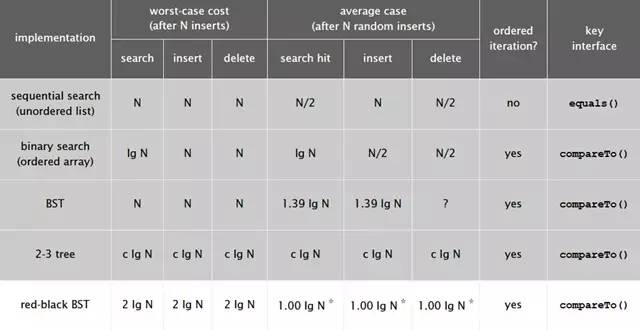
紅黑樹這種數據結構應用十分廣泛,在多種編程語言中被用作符號表的實現,如:
Java中的java.util.TreeMap,java.util.TreeSet;
C++ STL中的:map,multimap,multiset;
.NET中的:SortedDictionary,SortedSet等。
5.4 B樹和B+樹(B Tree/B+ Tree)
平衡查找樹中的2-3樹以及其實現紅黑樹。2-3樹種,一個節點最多有2個key,而紅黑樹則使用染色的方式來標識這兩個key。
維基百科對B樹的定義為“在計算機科學中,B樹(B-tree)是一種樹狀數據結構,它能夠存儲數據、對其進行排序并允許以O(log n)的時間復雜度運行進行查找、順序讀取、插入和刪除的數據結構。B樹,概括來說是一個節點可以擁有多于2個子節點的二叉查找樹。與自平衡二叉查找樹不同,B樹為系統最優化大塊數據的讀和寫操作。B-tree算法減少定位記錄時所經歷的中間過程,從而加快存取速度。普遍運用在數據庫和文件系統。
B樹定義:
B樹可以看作是對2-3查找樹的一種擴展,即他允許每個節點有M-1個子節點。
根節點至少有兩個子節點
每個節點有M-1個key,并且以升序排列
位于M-1和M key的子節點的值位于M-1 和M key對應的Value之間
其它節點至少有M/2個子節點
下圖是一個M=4 階的B樹:
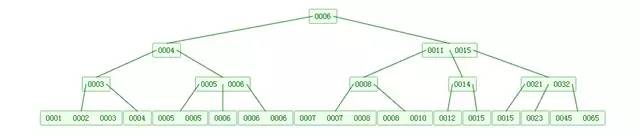
可以看到B樹是2-3樹的一種擴展,他允許一個節點有多于2個的元素。B樹的插入及平衡化操作和2-3樹很相似,這里就不介紹了。下面是往B樹中依次插入
6 10 4 14 5 11 15 3 2 12 1 7 8 8 6 3 6 21 5 15 15 6 32 23 45 65 7 8 6 5 4
B+樹定義:
B+樹是對B樹的一種變形樹,它與B樹的差異在于:
有k個子結點的結點必然有k個關鍵碼;
非葉結點僅具有索引作用,跟記錄有關的信息均存放在葉結點中。
樹的所有葉結點構成一個有序鏈表,可以按照關鍵碼排序的次序遍歷全部記錄。
如下圖,是一個B+樹:
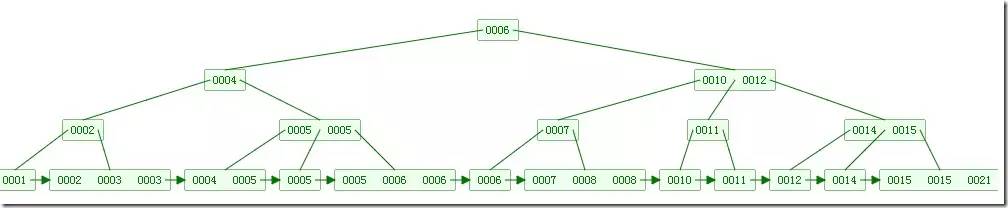
B和B+樹的區別在于,B+樹的非葉子結點只包含導航信息,不包含實際的值,所有的葉子結點和相連的節點使用鏈表相連,便于區間查找和遍歷。
B+ 樹的優點在于:
由于B+樹在內部節點上不好含數據信息,因此在內存頁中能夠存放更多的key。 數據存放的更加緊密,具有更好的空間局部性。因此訪問葉子幾點上關聯的數據也具有更好的緩存命中率。
B+樹的葉子結點都是相鏈的,因此對整棵樹的便利只需要一次線性遍歷葉子結點即可。而且由于數據順序排列并且相連,所以便于區間查找和搜索。而B樹則需要進行每一層的遞歸遍歷。相鄰的元素可能在內存中不相鄰,所以緩存命中性沒有B+樹好。
但是B樹也有優點,其優點在于,由于B樹的每一個節點都包含key和value,因此經常訪問的元素可能離根節點更近,因此訪問也更迅速。
下面是B 樹和B+樹的區別圖:
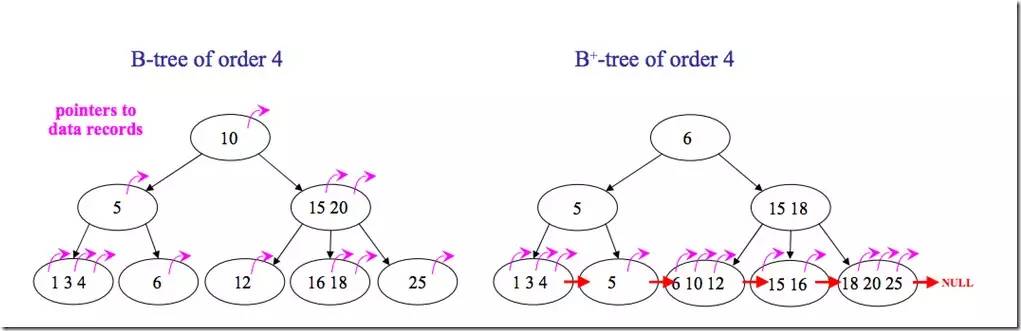
B/B+樹常用于文件系統和數據庫系統中,它通過對每個節點存儲個數的擴展,使得對連續的數據能夠進行較快的定位和訪問,能夠有效減少查找時間,提高存儲的空間局部性從而減少IO操作。它廣泛用于文件系統及數據庫中,如:
Windows:HPFS文件系統;
Mac:HFS,HFS+文件系統;
Linux:ResiserFS,XFS,Ext3FS,JFS文件系統;
數據庫:ORACLE,MYSQL,SQLSERVER等中。
有關B/B+樹在數據庫索引中的應用,請看張洋的MySQL索引背后的數據結構及算法原理這篇文章,這篇文章對MySQL中的如何使用B+樹進行索引有比較詳細的介紹,推薦閱讀。
樹表查找總結:
二叉查找樹平均查找性能不錯,為O(logn),但是最壞情況會退化為O(n)。在二叉查找樹的基礎上進行優化,我們可以使用平衡查找樹。平衡查找樹中的2-3查找樹,這種數據結構在插入之后能夠進行自平衡操作,從而保證了樹的高度在一定的范圍內進而能夠保證最壞情況下的時間復雜度。但是2-3查找樹實現起來比較困難,紅黑樹是2-3樹的一種簡單高效的實現,他巧妙地使用顏色標記來替代2-3樹中比較難處理的3-node節點問題。紅黑樹是一種比較高效的平衡查找樹,應用非常廣泛,很多編程語言的內部實現都或多或少的采用了紅黑樹。
除此之外,2-3查找樹的另一個擴展——B/B+平衡樹,在文件系統和數據庫系統中有著廣泛的應用。
6. 分塊查找
分塊查找又稱索引順序查找,它是順序查找的一種改進方法。 算法思想:將n個數據元素"按塊有序"劃分為m塊(m ≤ n)。每一塊中的結點不必有序,但塊與塊之間必須"按塊有序";即第1塊中任一元素的關鍵字都必須小于第2塊中任一元素的關鍵字;而第2塊中任一元素又都必須小于第3塊中的任一元素,…… 算法流程: step1 先選取各塊中的最大關鍵字構成一個索引表; step2 查找分兩個部分:先對索引表進行二分查找或順序查找,以確定待查記錄在哪一塊中;然后,在已確定的塊中用順序法進行查找。
7. 哈希查找
什么是哈希表(Hash)?
我們使用一個下標范圍比較大的數組來存儲元素。可以設計一個函數(哈希函數, 也叫做散列函數),使得每個元素的關鍵字都與一個函數值(即數組下標)相對應,于是用這個數組單元來存儲這個元素;也可以簡單的理解為,按照關鍵字為每一個元素"分類",然后將這個元素存儲在相應"類"所對應的地方。但是,不能夠保證每個元素的關鍵字與函數值是一一對應的,因此極有可能出現對于不同的元素,卻計算出了相同的函數值,這樣就產生了"沖突",換句話說,就是把不同的元素分在了相同的"類"之中。后面我們將看到一種解決"沖突"的簡便做法。
總的來說,"直接定址"與"解決沖突"是哈希表的兩大特點。
什么是哈希函數?
哈希函數的規則是:通過某種轉換關系,使關鍵字適度的分散到指定大小的的順序結構中,越分散,則以后查找的時間復雜度越小,空間復雜度越高。
算法思想:哈希的思路很簡單,如果所有的鍵都是整數,那么就可以使用一個簡單的無序數組來實現:將鍵作為索引,值即為其對應的值,這樣就可以快速訪問任意鍵的值。這是對于簡單的鍵的情況,我們將其擴展到可以處理更加復雜的類型的鍵。
算法流程:
1)用給定的哈希函數構造哈希表;
2)根據選擇的沖突處理方法解決地址沖突;
常見的解決沖突的方法:拉鏈法和線性探測法。詳細的介紹可以參見:淺談算法和數據結構: 十一 哈希表。
3)在哈希表的基礎上執行哈希查找。
哈希表是一個在時間和空間上做出權衡的經典例子。如果沒有內存限制,那么可以直接將鍵作為數組的索引。那么所有的查找時間復雜度為O(1);如果沒有時間限制,那么我們可以使用無序數組并進行順序查找,這樣只需要很少的內存。哈希表使用了適度的時間和空間來在這兩個極端之間找到了平衡。只需要調整哈希函數算法即可在時間和空間上做出取舍。
復雜度分析:
單純論查找復雜度:對于無沖突的Hash表而言,查找復雜度為O(1)(注意,在查找之前我們需要構建相應的Hash表)。
使用Hash,我們付出了什么? 我們在實際編程中存儲一個大規模的數據,最先想到的存儲結構可能就是map,也就是我們常說的KV pair,經常使用Python的博友可能更有這種體會。使用map的好處就是,我們在后續處理數據處理時,可以根據數據的key快速的查找到對應的value值。map的本質就是Hash表,那我們在獲取了超高查找效率的基礎上,我們付出了什么?
Hash是一種典型以空間換時間的算法,比如原來一個長度為100的數組,對其查找,只需要遍歷且匹配相應記錄即可,從空間復雜度上來看,假如數組存儲的是byte類型數據,那么該數組占用100byte空間。現在我們采用Hash算法,我們前面說的Hash必須有一個規則,約束鍵與存儲位置的關系,那么就需要一個固定長度的hash表,此時,仍然是100byte的數組,假設我們需要的100byte用來記錄鍵與位置的關系,那么總的空間為200byte,而且用于記錄規則的表大小會根據規則,大小可能是不定的。
Hash算法和其他查找算法的性能對比:
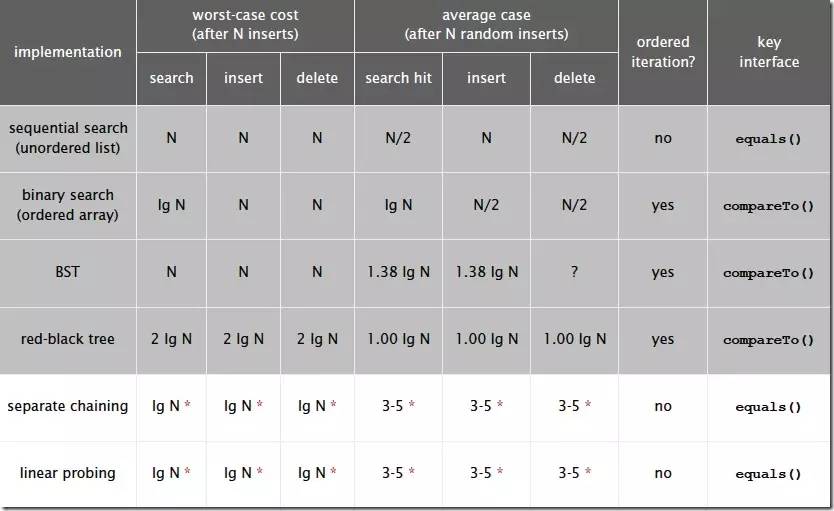
-
算法
+關注
關注
23文章
4615瀏覽量
93000 -
adas
+關注
關注
309文章
2185瀏覽量
208688 -
查找
+關注
關注
0文章
5瀏覽量
8411
發布評論請先 登錄
相關推薦






 詳細介紹ADAS算法
詳細介紹ADAS算法











評論