多級分層分區和實現涉及包含內部物理子分區的分區。換句話說,在這種方法中,對分區本身進行分層分割。考慮SoC分區方案的示例,如圖1所示。級別0對應于整個芯片的單個平面實現,其中唯一被建模的物理接口是與外部世界有關的那個(以藍色顯示)。換句話說,在芯片內部,只有邏輯邊界,沒有物理邊界。

圖1:SoC中典型的多級分層分區方案
跨越核心,APP_SUB_SYSTEM等的內部邏輯交互(以黑色顯示)因此被覆蓋在平面設計本身內。這種類型的方案本身具有最小的接口預算復雜性(在下一節中討論),涉及分區間交互,因為只有一個分區。但是,這種方案不適用于大型設計,主要是由于EDA工具運行時間,內存和機器資源要求的限制。
為了簡化這種設計方案,設計人員可以選擇使用單級分層分區如第1級所示。在這種情況下,設計人員最終會得到4個物理分區或塊,如表1所示。在這種方法中,工程資源方面的設計限制被放寬,但是分區間路徑變得更加復雜,就預算而言,需要特別小心。將0級與1級進行比較,我們觀察到在0級時只有外部接口路徑導致了主要的不確定性,在1級中,幾乎所有的分區間路徑都為我們提供了I/O接口的類似不確定性和復雜性。然而,級別1和級別0(外部接口)的接口路徑的性質或多或少相似,因此可以使用相同的方法和約束來對它們進行建模。級別0和級別1接口路徑之間存在非常重要的差異。 0級接口路徑由協議控制,其中一些協議具有為SoC給出的明確預算。 SoC只能遵守這些預算。另一方面,對于塊間路徑,預算編制位于設計者手中。沒有標準協議來管理交互,預算分配通常是迭代的。
轉向第2級,我們進一步將第1級的分區劃分為更小的子塊。有了這個,我們最終留下了7個獨特的物理分區。這大大有助于減少工具運行時間和資源限制,因為設計已經分解成更小的部分;但是類似于1級,分區間路徑&不確定性也在增加。在級別1的情況下,我們能夠模擬類似于級別0的外部接口的分區接口;第2級帶有更復雜的接口時序和實現,特別是如果涉及的路徑跨越多個分區。此外,優化的好處也顯著降低,因為跨物理邊界的優化不會非常有效。
因此,在改進時序和實現關閉方面,多級分區通常可能是賭博。這種策略的回報取決于接口建模技術的質量以及物理分區本身所涉及的邏輯的成熟度曲線。在下一節中,我們將討論有關多級分區方案的一些獨特挑戰及其可能的解決方案(如果有的話)。
表I:圖1所示設計中各種分區的層次結構級別。
TOP(1)
| 分區級別 | LEVEL 0(實例計數) | LEVEL 1(實例計數) | LEVEL 2(實例計數) |
|
分層 塊 |
TOP_SOG(1) | TOP_SOG(1) | |
| DUAL_CORE_TOP(2) | DUAL_CORE_TOP (2)+核心(4) | ||
| GENERIC I/O CONTROLLER(2) | GENERIC I/O控制器(2)+IO_FIFO(2) | ||
| APP_SUB_SYSTEM(1) | APP_SUB_SYSTEM(1)+APP_CORE(1) | ||
| 總分區計數 | 1個唯一的 | 2唯一+ 2復制 | 3個唯一+4個重復 |
多級分層時序收斂和實施中的挑戰
分層時序收斂固有地存在其缺點,主要是由物理邊界上的界面不確定性和波紋效應驅動。除了計時,物理限制進一步造成了實施周期的其他方面的瓶頸,如平面圖關閉,引腳布局,泄漏減少等。負責這些的主要因素可分為以下幾類:
a)物理不確定性:
物理不確定性反映了由物理隔離引起的關閉不確定性在實現期間的分層分區。物理不確定性通常由于三個因素而產生:
i。跨接口的不可預測的數據路徑分布:
跨分區邊界的數據路徑分布在很大程度上取決于分區的物理成熟度和邏輯成熟度。由于這種不可預測性而出現的最常見挑戰之一是跨接口邊界的輸入/輸出延遲的復雜和迭代預算。除此之外,基于附加階段的放置,CTS和路由跳躍的不確定性進一步使這個簡單的任務更加迭代和依賴于實現。讓我們考慮多級分區APP_SUB_SYSTEM的例子,如圖1所示。我們可以清楚地看到,在TOP_SOG界面,有兩類交互:APP_SUB_SYSTEM與TOP_SOG& APP_CORE與TOP_SOG可以建模如下:
APP_SUB_SYSTEM - TOP_SOG預算公式:
的 的的
Logic_Distribution_Inside_APP_SUB_SYSTEM
+ Stage_Margin_APP_SUB_SYSTEM
+ Stage_Margin_TOP_SOG
APP_CORE - TOP_SOG預算公式:
Logic_Distribution_Inside_APP_CORE
+ Stage_Margin_APP_CORE
+ Stage_Margin_APP_SUB_SYSTEM
+ Logic_Distribution_Inside_APP_SUB_SYSTEM
+ Stage_Margin_TOP_SOG
上面的等式只是建議在為子預算建模時在多級分區設計中,必須考慮所有中間分區的階段余量和邏輯分布(即路徑開始和結束分區除外)。如果預算是從最高層開始的,那么這個預算也必須合理地分成相似的部分,以便正確實施和時間關閉。例如,讓我們假設頂部給出了一個10ns的裕度(時鐘周期的50%)到APP_CORE的IN2REG路徑,時鐘為20ns。現在,假設80%的邏輯位于APP_CORE內,而剩余的20%位于APP_SUB_SYSTEM內作為直通路徑,這意味著在任何階段APP_SUB_SYSTEM內的預算不應超過2ns,對于APP_CORE,它應限制在8ns。除此之外,還必須在此限制內對單個塊階段余量進行建模。
因此,設計人員必須將此路徑建模為:
APP_CORE的I/P最大延遲= 20 - (0.8 * 10)= 12ns
I/P_port_budget + APP_CORE_stage_margin= 12ns
對于APP_SUB_SYSTEM的I/P到O/P最大延遲= 0.2 * 10 = 2ns
I/P_to_O/P_port_budget + APP_SUB_SYSTEM_margin= 2ns
雖然上述計算看起來相當簡單,但問題在設計成熟,邏輯分布以及階段邊距發生變化時開始。因此,在多分區方案中,每個后續分區的數量變量將增加至少2,這通常會迫使設計人員進行多次迭代以使這些預算成熟,以實現正確的收斂時序收斂。
II。分區邊界內外的不常見路徑:
除邏輯分布外,不常見的時鐘路徑是另一個噩夢,在分層關閉的情況下困擾設計者。雖然不常見的路徑不確定性的建模是與預算分布類似的類型的挑戰,但是更加有害的方面來自與不常見路徑相關聯的不匹配的形式。不常見路徑的一些常見后果是:
CPPR或CPPR降級的變化。
輸入延遲的變化以及I/O建模
接口保持違規的大幅增加
由于時間窗口的變化引起的噪聲變化
解決此類不匹配的唯一方法是減少跨越分區的不常見路徑,并嘗試對其進行建模,同時考慮與之相關的所有類型的不確定性。但是,隨著分區級別的增加,不常見路徑的建模和減少都會成為設計人員面臨的主要挑戰。在大多數情況下,由于非常見路徑的余量通常有點悲觀,因此當我們達到最低級別的分區時,通過每個分區級別關聯的次要悲觀傾向于累積到主要塊中。
圖2顯示了一個典型示例,其中可以輕松地看到跨分區層次結構的不常見路徑的變化。對于頂級分區TOP_SOG,非常見路徑在Z之后立即開始,其中進一步進入APP_SUB_SYSTEM的層次結構,APP_CORE分別為Y和X.這意味著與TOP_SOG相比,在APP_CORE上應用時鐘降額的影響要小得多,因此導致時序不匹配,這可能導致跨接口的保持違規大幅增加,并且由于APP_CORE與APP_SUB_SYSTEM不匹配而產生噪聲變化。本身與TOP_SOG不匹配。
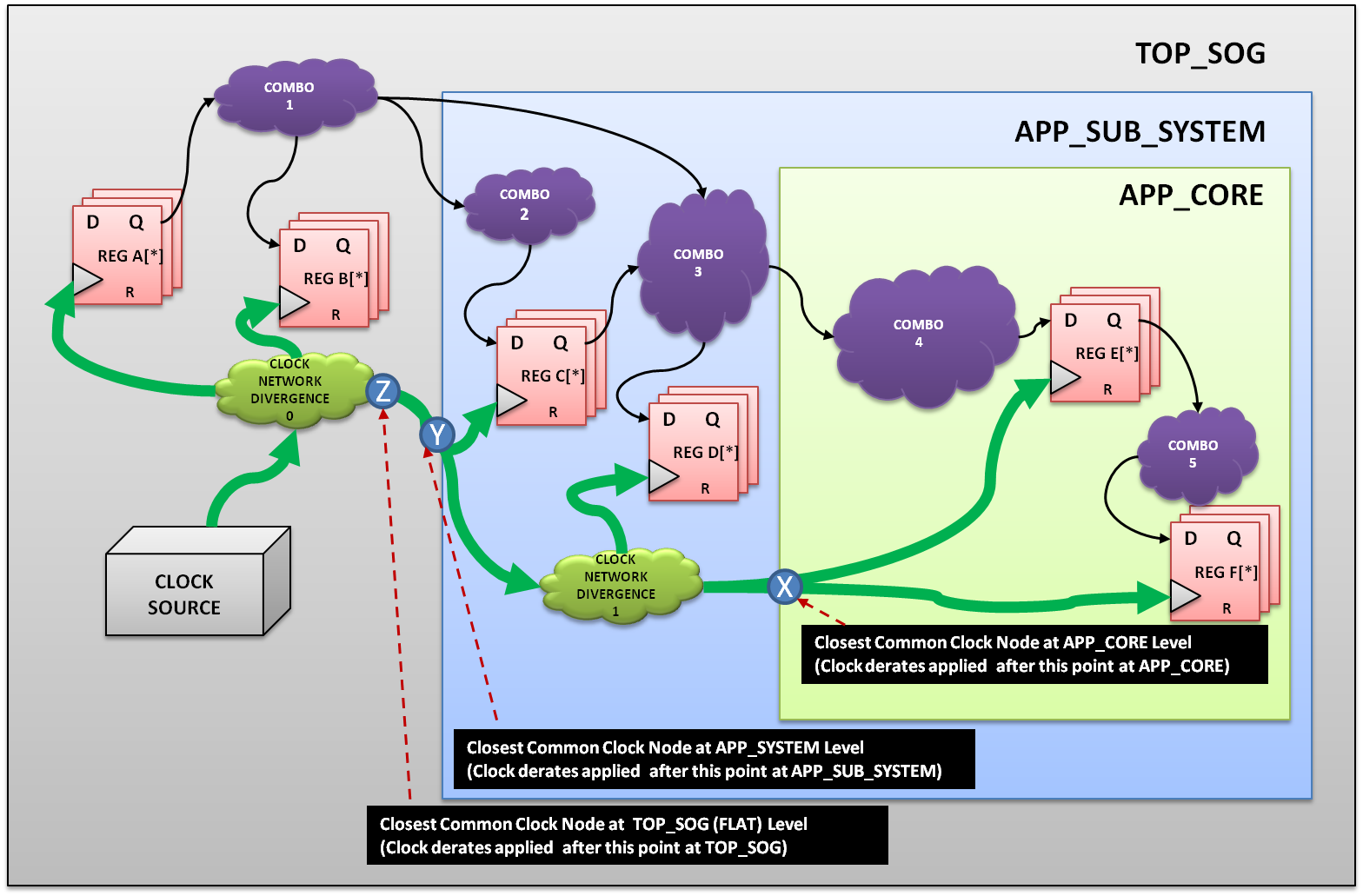
圖2:多級分層設計中不常見和常見路徑的影響。
iii。常見路徑不匹配:
之前我們討論了多級分區設計中不常見路徑的不利影響,但是與外部接口相關的公共路徑也同樣關注,特別是在噪音分析的情況下。公共路徑延遲的簡單改變可以在正常分析中傳遞小的CPPR調整,然而,這種延遲的改變可能在早先沒有貢獻的時序窗口中產生重疊;因此,降低噪聲分布并在甚至REG2REG內部路徑中產生違規,這些路徑早先遇到噪聲。引入更多級別的分區進一步增加了這種不匹配的可能性,因此即使在噪聲之后也會對塊級設計閉合的質量產生懷疑。
考慮REG_REG路徑跨越REG E和REG F在APP_CORE中如圖所示圖2.這是APP_CORE的完全內部路徑,但是由于公共路徑本身(直到X)的變化,從TOP_SOG和APP_SUB_SYSTEM級別看時鐘邊緣到達時延遲的變化會產生完全不同的時序窗口重疊,如圖所示雖然這些路徑可以通過過度優化來修復,以模擬這種不匹配,但仍然在設計執行期間,人們永遠無法確定公共路徑是否保持不變。
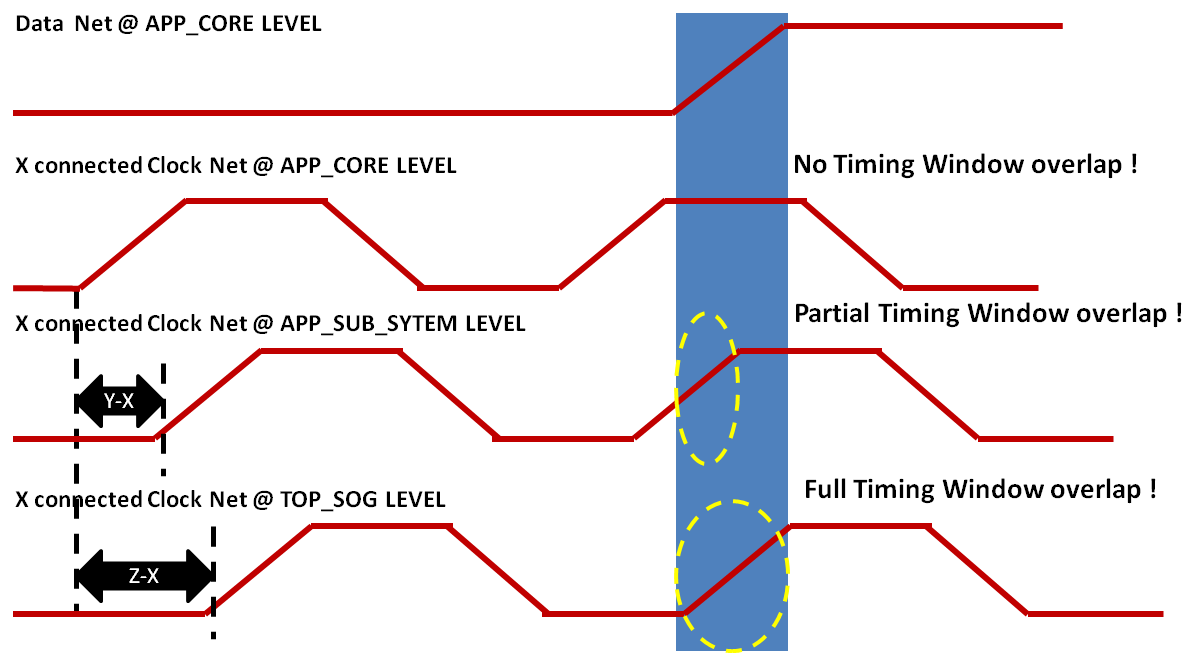
圖3:共用路徑對多級分層設計中SI(噪聲)時序窗口的影響。
b)物理限制:
在多級分區中作為物理分區的數量增加,因為物理限制導致放置問題。物理限制通常反映在有限的端口/引腳/宏放置或建模中。以下是在處理物理挑戰時應考慮的一些關鍵點:
i。塊和子塊的所有相同端口應放置在附近,它們之間的布局邏輯最小。這些端口通常用于為TOP和子塊提供連接,因此應使用最小緩沖區并且應非常小心地處理放置。循環路徑中涉及的端口,宏和邏輯的放置,即in2reg,然后是reg2out,反之亦然,應該通過考慮時間以及DRV和DRC的合理余量來驅動,因為這些很可能是瓶頸。后期設計階段。
iii。子塊可能存在一些時序模型問題。例如,當使用典型的物理實現EDA工具(如Cadence EDI)時,我們通常會為子塊指定接口邏輯模型(ILM)。使用ILM時,有一些端口(復位,掃描啟用等),由于其大小限制,其相關邏輯未被轉儲到ILM內部(復位轉到所有觸發器,因此如果在ILM中保留復位邏輯,則ILM壓縮將為低)。這導致在相同端口之間留下未優化的邏輯,因為它在EDI端不可見,如圖4所示。為解決此類情況,可以使用以下一些替代方案:
在較高層次分區內的此類端口之間設置最大延遲,其預算取決于它們的定時時鐘。在多個時鐘的情況下,我們需要給它們最壞的情況預算,以便信號可以從塊端口到達子塊。
如果有少數端口正在通話并且它們之間具有未優化的邏輯,我們可以手動更改該邏輯,以便它們花費最少的時間并將它們設置為在實現端不接觸。然而,這種方法并不是一個明確的長期解決方案,因為在每次優化之后生成手動定時ECO可能會變得很麻煩。
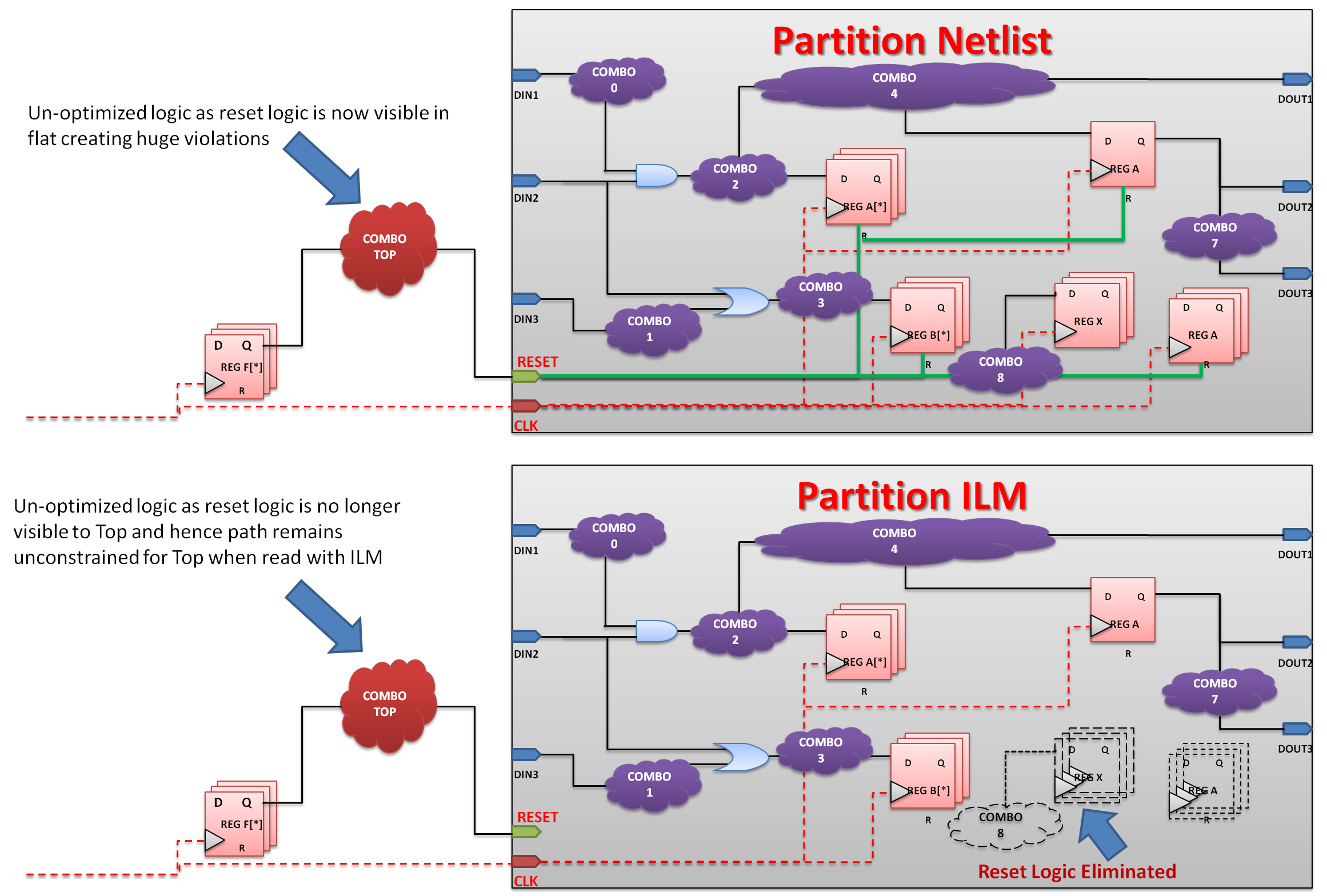
圖4:基于ILM建模的未優化復位路徑。
c)亞優化優化&復制問題:
次優優化是分層設計的主要實現相關限制。隨著硬分區數量的增加,對邊界和接口邏輯的優化也會增加。當大量使用這種分區的復制塊時,這成為一個更令人擔憂的問題。考慮圖1中的 dual_core_top 模塊。與內部邏輯定時相比,兩個復制內核中的接口邏輯仍然沒有那么優化。
因此,如果用戶要離開示波器25mW泄漏減少,對于單個核心似乎是一個小問題,但是將其乘以復制品的數量,在圖1的設計中,用戶現在錯過了相當于4 * 25 = 100mW的泄漏減少平面設計。此外,對于復制的分區,設計人員主要有兩個選項,要么針對最壞情況優化塊,要么針對常見場景對其進行優化。對于前者,設計師很可能最終不會優化設計,而對于后者,設計師可能最終會遇到可能無法輕易解決的問題。
例如,假設a公共存儲器數據總線到達四核頂部分區的4個核心,如圖5所示。現在由于物理位置,核心4的時鐘延遲和總線數據偏差可能比core1高200-250ps。現在對于略微滿足的路徑,這可能會導致最佳角落中最近的core1的額外保持違規,而core4中的設置違規在最壞的角落中最遠,而在core2和core3處不會出現此類違規。因此,如果設計者選擇修復這些違規,盡管沒有核心具有相同的設置以及關鍵路徑,但是由于復制和物理放置,這種情況仍然可能存在。
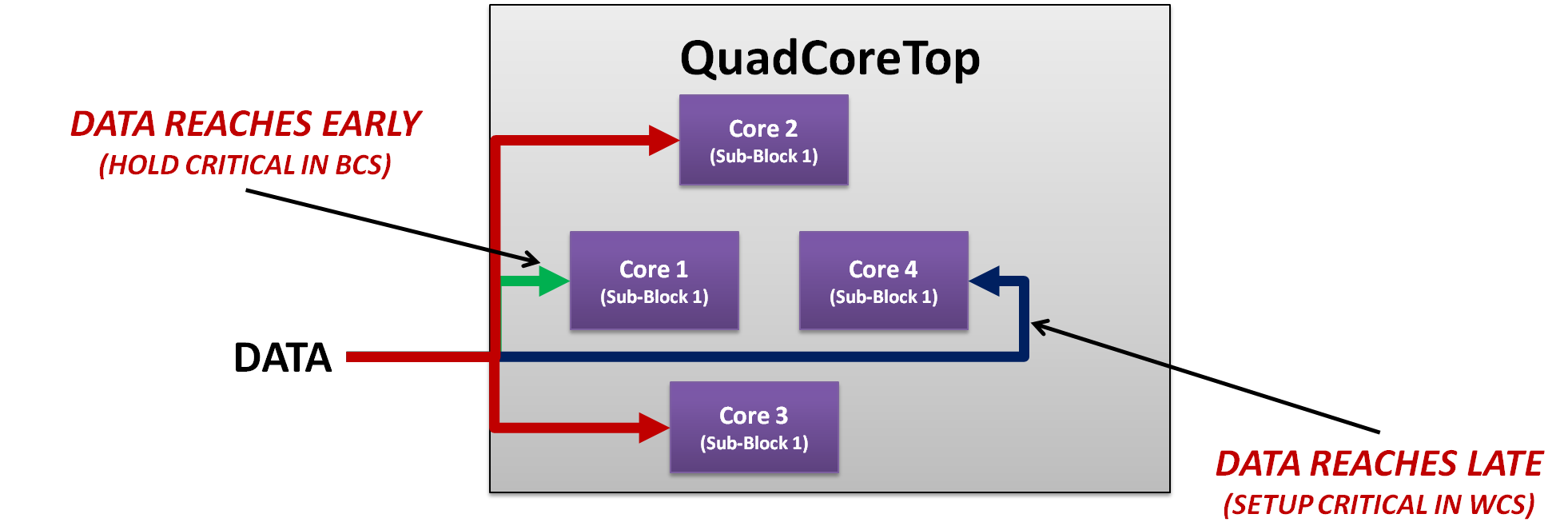
圖5:復制在四核類似塊內的多級分層分區中的影響。
-
PCB打樣
+關注
關注
17文章
2968瀏覽量
21742 -
華強PCB
+關注
關注
8文章
1831瀏覽量
27811 -
華強pcb線路板打樣
+關注
關注
5文章
14629瀏覽量
43087
發布評論請先 登錄
相關推薦
關于功能驗證、時序驗證、形式驗證、時序建模的論文
FPGA學習指南合集:Verilog HDL那些事兒(建模篇,時序篇,整合篇)
多片段時序數據建模預測實踐資料分享
一種分層遞階機制的實時多層建模方法
基于Linux 的兩種分層存儲實現方案
RP Fiber Power中的多級放大器建模方案解析





 多級分層分區和建模方案中涉及的主要時序和實現挑戰
多級分層分區和建模方案中涉及的主要時序和實現挑戰











評論