節點分析

節點分析是一種分析形式，它使用基爾霍夫電流定律（KCL）和節點方程來求解電路電壓值，其中原理圖沒有任何導體路徑交叉。通常用于此目的的術語稱為平面電路。

這用于確定每個節點（或兩個或多個組件的連接點）的電壓尊重參考節點。參考節點通常稱為地，其中地電壓等于零伏。

在查看電壓源或電流源的示意圖時，參考節點通常是當為電流源示出箭頭時，將其分配給電壓源的負端子和相對端。選擇參考節點的另一種方法是在查看所有節點時選擇中間節點。

有兩種電源：1）獨立和2）依賴。

獨立源為連接的電路提供固定的電壓或電流值。獨立的來源是電源和電池。電源提供恒定的固定值，而電池在沒有充電的情況下不會提供恒定的固定值。

從屬源是電壓源或電流源，其值取決于根據電路中其他地方的電壓或電流值。相關源是分析放大器的有用工具。放大器的兩個特性是電壓增益（A V ）和電流增益（Ai）。有四種基本的線性相關來源：

1。輸出為V的電壓控制電壓源，A V 是比例常數（電壓增益），V CD 是被檢測的參數。以下等式與壓控電壓源相關：

$$ V = A_ {V} V_ {CD} $$

2。電流控制電壓源，其中輸出為V，R M 是比例常數（電阻），I C 是被感測的參數。以下等式與電流控制電壓源相關：

$$ V = R_ {M} I_ {C} $$

3。電流控制電流源，其中輸出為I，Ai是比例常數（電流增益），I C 是被感測的參數。以下等式與電流控制電流源相關：

$$ I = A_ {I} I_ {C} $$

4。輸出為I的壓控電流源，GM是比例常數（電導），VCD是被檢測的參數。以下公式與壓控電流源相關：

$$ I =（G_ {M}）（V_ {CD}）$$

如圖1所示，當有兩個直流電壓源和一個直流電流源時，會發生一個依賴源的節點分析。注意，E1的值用未知值表示。 E1 = 2Vx。注意，電阻器R1兩端的電壓表示為Vx。注意，電阻器R3兩端的電壓表示為V0。此信息稍后將用于計算節點電壓。

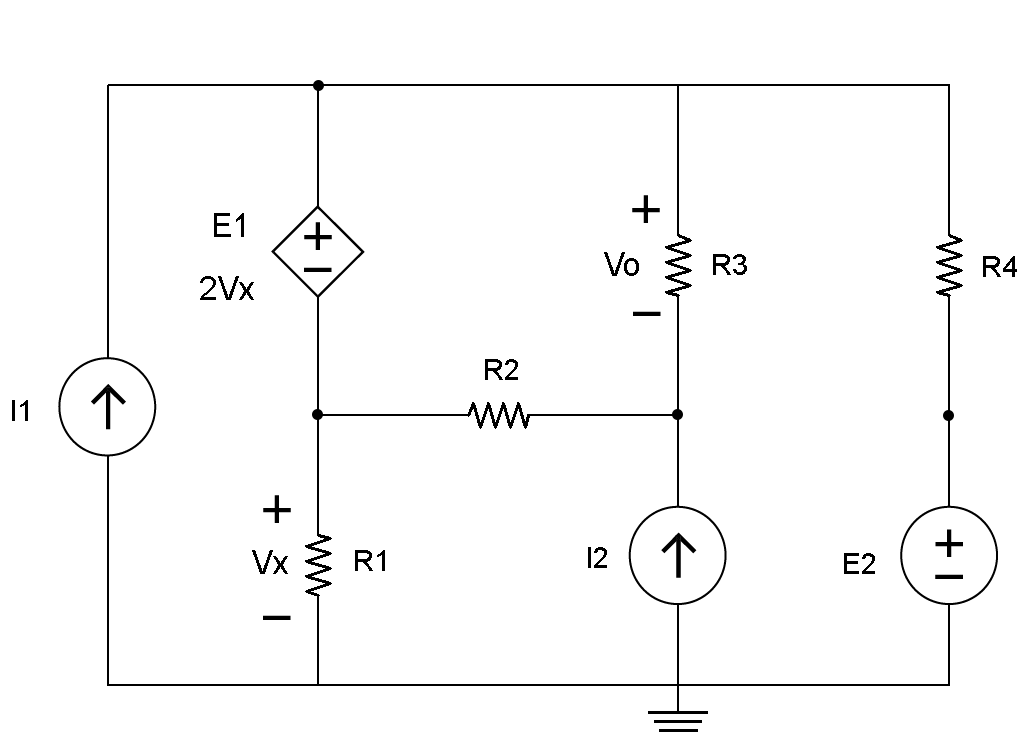
圖1

如果節點或測試點電壓為正，它將讀取電壓表上的正值。如果節點或測試點電壓為負，它將讀取電壓表上的負值。

圖1所示電路的一個示例問題是找到以下內容：

一個。電阻R3兩端的電壓（V0）。

B.電流通過電阻R1（IR1），R2（IR2），R3（IR3）和R4（IR4）。

C.設I1 = 2 mAmps，I2 = 2 mAmps，E1 = 2Vx，E2 = 4 V，R1 = 1 Kilo歐姆，R2 = 2千歐，R3 = 3千歐，R4 = 4千歐。

d。設R1（ER1）上的電壓= Vx，E1 = V1 - V2。

第一步是識別參考節點或地面，然后是所有節點。圖1中顯示了電路。通常任何獨立的源都接地，如圖1所示。

在這個電路中，DC電壓源頂部的節點標記為V1，標記為V1，低于E1在標記為V3的電阻器R3下方，以及在標記為V4的DC源E2上方。這些節點如圖2所示。

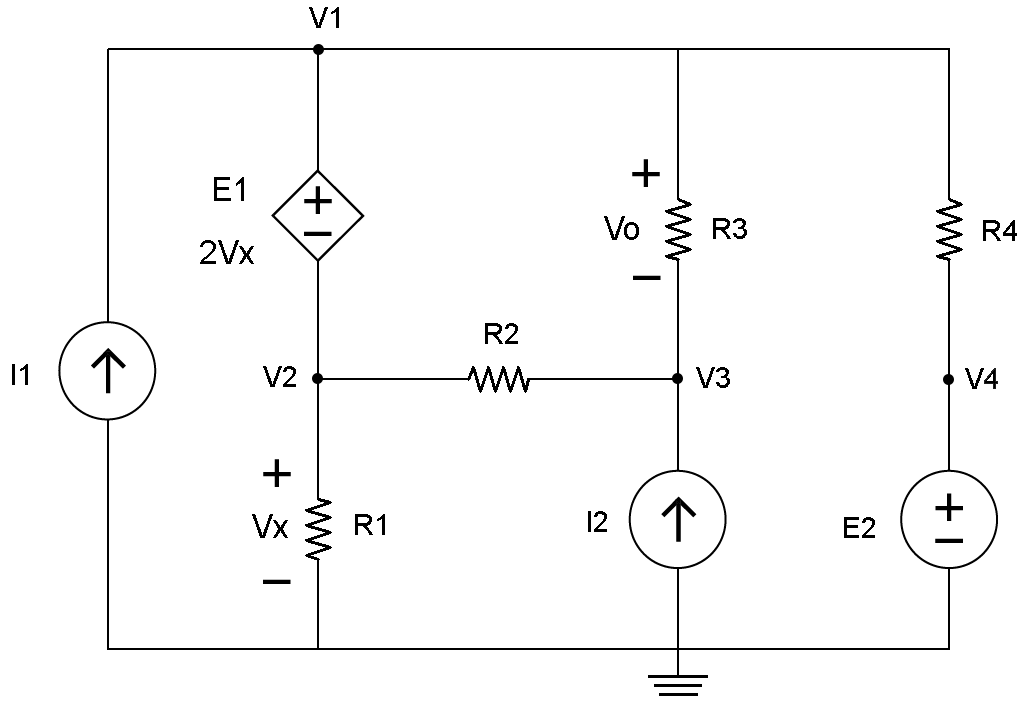
圖。 2

第二步是識別超級節點，該節點的從屬源具有未知的E1值，等于2Vx。在V1和V2周圍繪制一條紅線，其中E1如圖3所示。

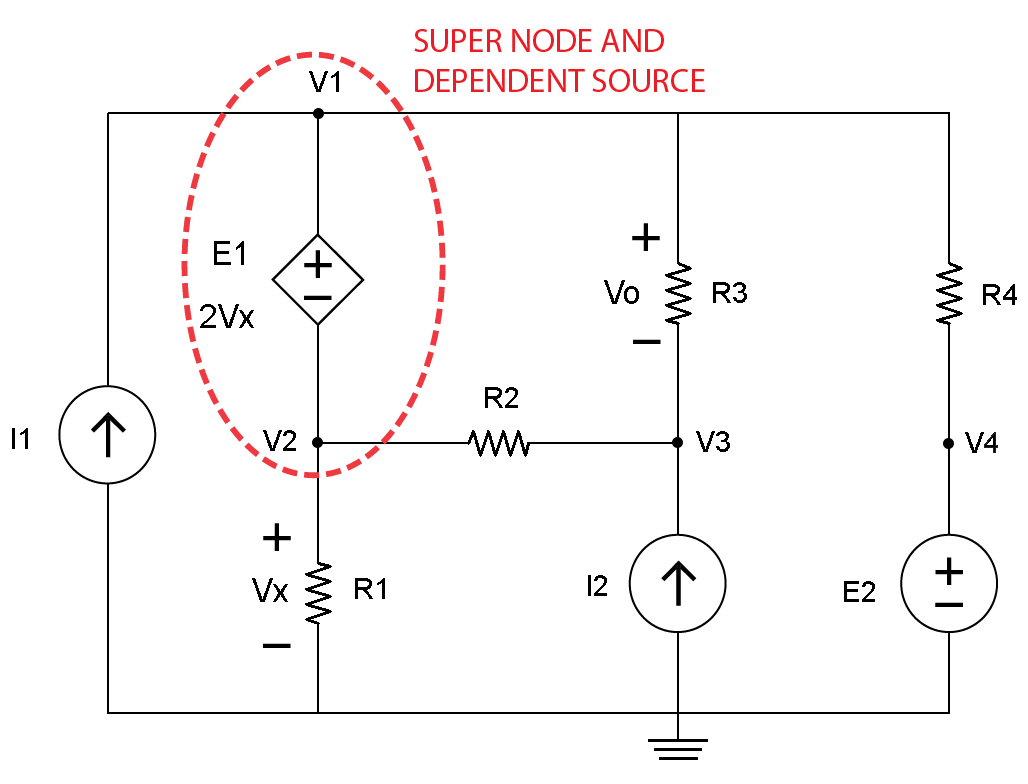
圖。 3

第三步是確定獨立源，即電壓源E2，以及電流源I1和I2。在V4和E2，I1和I2周圍畫一條藍線，如圖4所示。

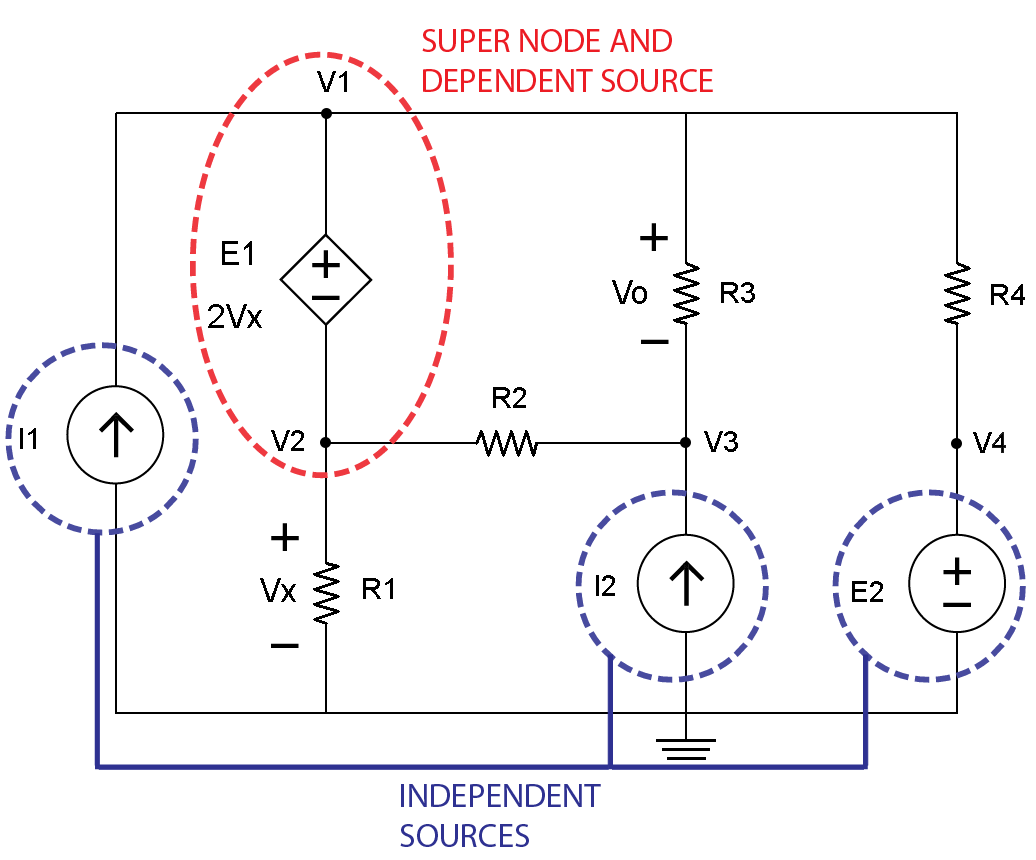
圖。 4

第4步是識別超級節點的電流，藍線和箭頭標記為a，b，c，d和e，如圖5所示。

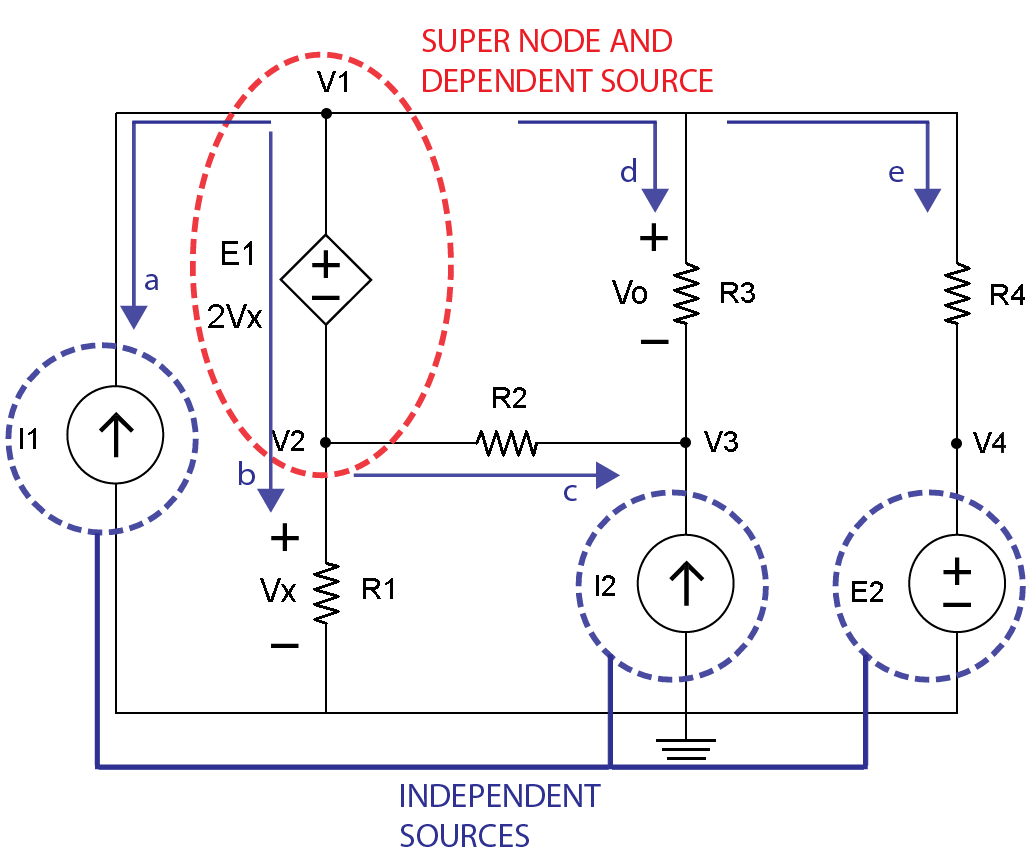
圖5

第五步是識別V3節點的電流，紅線和箭頭標記為f，g和h，如圖6所示。

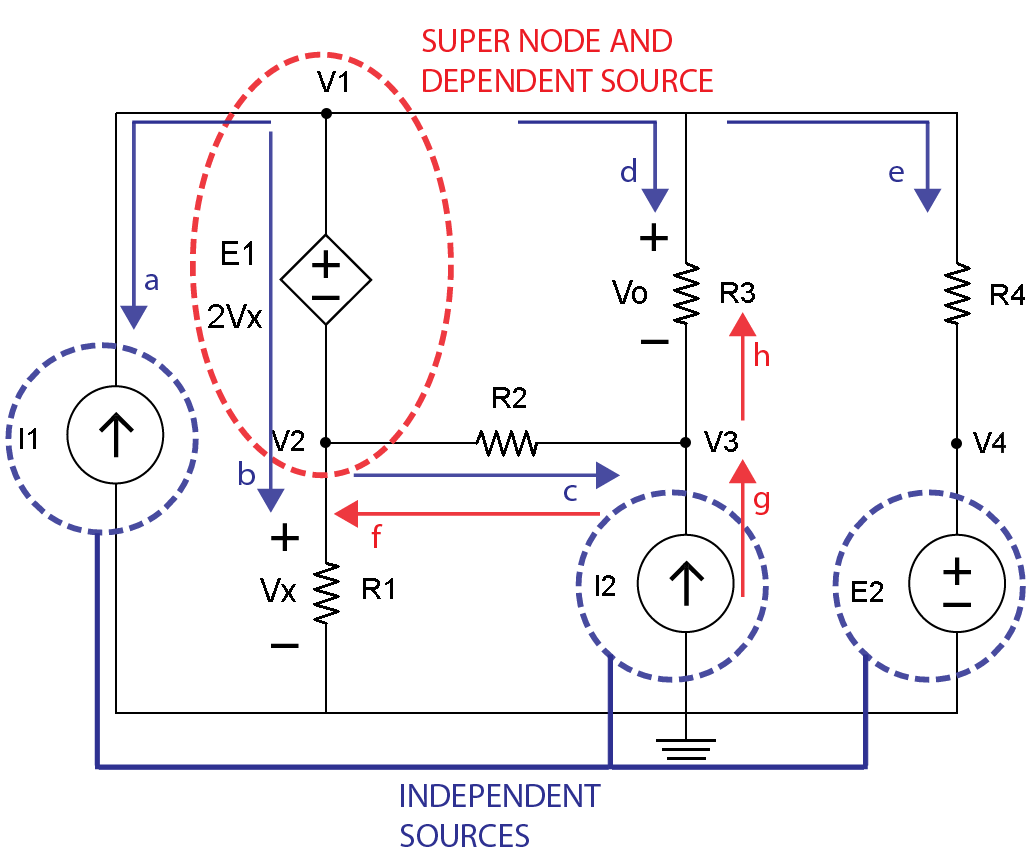
圖6

下一步將利用圖5標識超級節點，以便識別基爾霍夫電流定律（KCL）方程。請記住，基爾霍夫電流定律（KCL）規定進入和離開節點的所有電流的代數和必須等于零。

以下KCL電流方程可以寫入超級節點的藍線和箭頭a，b，c，d和e：

$$ -I_ {1} + I_ {b} + I_ {c} + I_ 5vgeo944t + I_ {e} = 0 $$

請注意：

$$ I_ {b} = \ frac {V_ {2}} {R_ {1}}，I_ {c} = \ frac {V_ {2} - V_ {3}} {R_ {2}}，I_ 5vgeo944t = \ frac {V_ {1} -V_ {3}} {R_ {3}}，I_ {e} = \ frac {V_ {1} - E_ {2}} {R_ {4}} $$

現在，等式變為：

$$ -I_ {1} + \ frac {V_ {2}} {R_ {1}} + \ frac {V_ {2} -V_ {3}} {R_ {2}} + \ frac {V_ {1} -V_ {3}} {R_ {3}} + \ frac {V_ { 1} -E_ {2}} {R_ {4}} = 0 $$

替換電路值：

$$ - （\ text {2 m}）+ \ frac {V_ {2}} {\ text {1 k}} + \ frac {V_ {2} -V_ {3}} {\ text {2k}} + \ frac {V_ {1} -V_ {3}} { \ text {3k}} + \ frac {V_ {1} -E_ {2}} {\ text {4k}} = 0 $$

將兩邊乘以12 k（Least CommonDenominator）：

$$ [ - （\ text {2 m}）+ \ frac {V_ {2}} {\ text {1 k}} + \ frac {V_ {2} -V_ {3}} { \ text {2k}} + \ frac {V_ {1} -V_ {3}} {\ text {3k}} + \ frac {V_ { 1} -E_ {2}} {\ text {4k}} = 0]（\ text {12 k}）$$

展開：

$$ - 24 + 12V_ {2} + 6（V_ {2} - V_ {3}）+ 4（V_ {1} - V_ {3}）+ 3（V_ {1} - 4）= 0 $$

$$ - 24 + 12V_ {2} + 6V_ {2} - 6V_ {3} + 4V_ {1} - 4 V_ {3} + 3V_ {1} - 12 = 0 $$

合并條款：

$$ 7V_ {1} + 18V_ {2} - 10V_ {3} = 36 $$ [等式1]

下一步將利用圖6顯示V3節點處的電流可以為f，g和h的紅線和箭頭寫出方程式。請注意，當查看c和g以及d和h的藍色和紅色線和箭頭時，通過電阻器R2和R3的電流方向是相反的。這在檢查結果后會很重要。

$$ -I_ {2} + \ frac {V_ {3} - V_ {2}} {R_ {2}} + \ frac {V_ { 3} -V_ {1}} {R_ {3}} = 0 $$

替換電路值：

$$ - （\ text {2 m}）+ \ frac {V_ {3} - V_ {2}} {\ text {2 k}} + \ frac {V_ {3} -V_ {1}} {\ text {3 k}} = 0 $$

將兩邊乘以6 k（最小公分母）：

$$ [ - （\ text {2 m}）+ \ frac {V_ {3} - V_ {2}} {\ text {2 k}} + \ frac {V_ {3} -V_ {1}} {\ text {3 k}} = 0]（\ text {6 k}）$$

展開：

$$ - 12 + 3（V_ {3} - V_ {2}）+ 2（V_ {3} - V_ {1}）= 0 $$

$$ - 12 + 3V_ {3} - 3V_ {2} + 2V_ {3} - 2V_ {1} = 0 $$

組合術語：

$$ - 2V_ {1} - 3V_ {2} + 5V_ {3} = 12 $$ [等式2]

有兩個方程和三個未知數。需要另一個等式。當查看圖5中有關直流電壓源E1和節點V2的給定信息以及電阻器R1上的電壓Vx時，可以得到另一個等式。

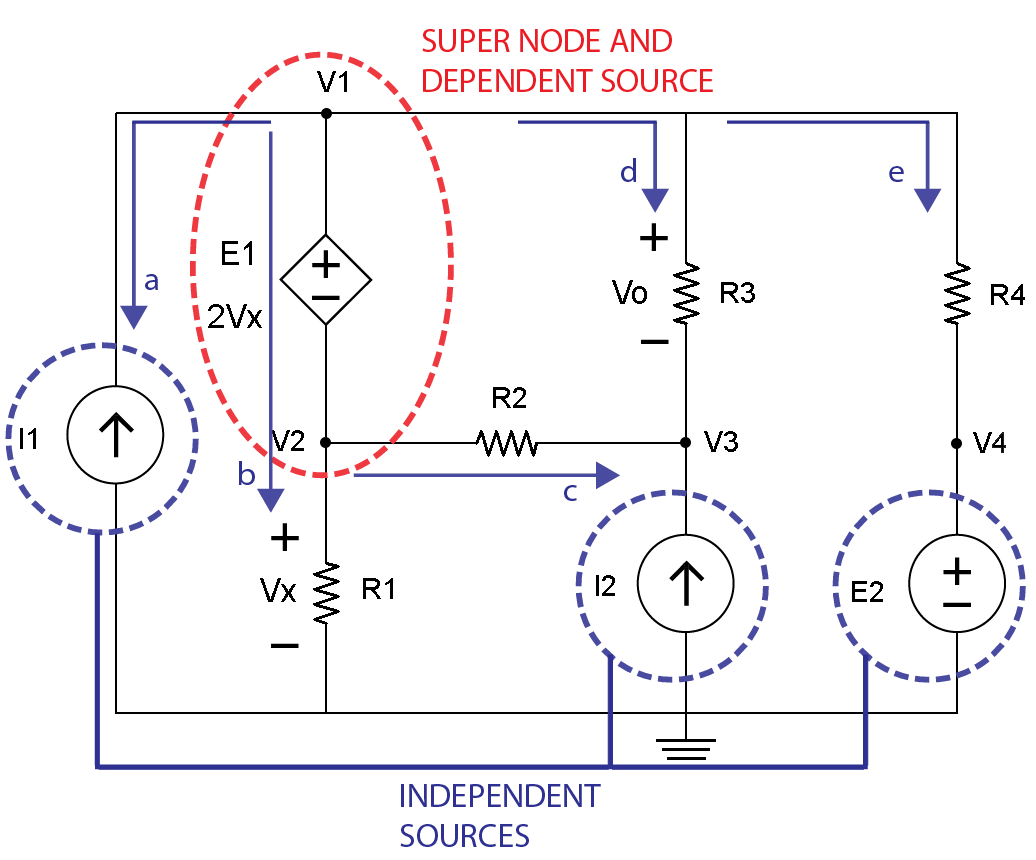
圖。 5

以下信息是已知的：

$$ E_ {1} = V_ {1} - V_ {2} $$

$$ E_ { 1} = 2V_ {X} $$

$$ V_ {1} - V_ {2} = 2V_ {X} $$ [等式A]

$$ V_ {2 } = V_ {X} $$ [公式B]

在公式A中使用公式B，其中V2 = Vx，可以得到V1的另一個公式：

$$ V_ {1 } - V_ {2} = 2V_ {X} $$

$$ V_ {1} - V_ {X} = 2V_ {X} $$

解決V1：

$$ V_ {1} = 2V_ {X} + V_ {X} $$

$$ V_ {1} = 3V_ {X} $$ [等式3]

現在，使用公式A和公式B，公式1和公式2需要以Vx和V3表示V1和V2項：

召回等式1：$$ 7V_ {1} + 18V_ {2} - 10V_ {3} = 36 $$

$$ 7（3V_ {X}）+ 18（V_ {X}） - 10V_ {3} = 36 $$

$$ 21V_ {X} + 18V_ {X} - 10V_ {3} = 36 $$

$$ 39V_ {X} - 10V_ {3} = 36 $$ [等式C]

召回等式2：$$ - 2V_ {1} - 3V_ {2} + 5V_ {3} = 12 $ $

$$ - 2（3V_ {X}） - 3（V_ {X}）+ 5V_ {3} = 12 $$

$$ - 6V_ {X} - 3V_ {X} + 5V_ {3} = 12 $$

$$ - 9V_ {X} + 5V_ {3} = 12 $$ [等式D]

現在有兩個方程和兩個可以求解的未知數。

$$ 39V_ {X} - 10V_ {3} = 36 $$ [方程C]

$$ - 9V_ {X} + 5V_ {3} = 12 $$ [等式D]

當在等式D的兩側乘以2時，兩個等式可以加在一起，導致V3項被取消，留下一個等式為一個未知。

將公式D的兩邊乘以2：

$$（ - 9V_ {X} + 5V_ {3} = 12）（2） $$

展開：

$$ - 18V_ {X} + 10V_ {3} = 24 $$ [公式D]

將新的公式D添加到公式C：

$$ 39V_ {X} - 10V_ {3} = 36 $$ [公式C]

$$ - 18V_ {X } + 10V_ { 3} = 24 $$ [公式D]

$$ 21V_ {X} = 60 $$

解決Vx：

$$ \ underline { V_ {X} = 2.86 \ text {v}} $$

召回：$$ V_ {2} = V_ {X} $$，替換$$ V_ {X} = 2.86 \ text {伏特} $$

$$ \ underline {V_ {2} = 2.86 \ text {v}} $$

召回：$$ V_ {1} = 3V_ {X} $$，替換$$ V_ {X} = 2.86 \ text {volts} $$

$ $ V_ {1} = 3（2.86 \ text {v}）$$

$$ \ underline {V_ {1} = 8.58 \ text {v}} $$

當使用公式1和V1和V2的計算值時，可以計算V3：

召回：$$ 7V_ {1} + 18V_ {2} - 10V_ {3} = 36 $$

替換V1和V2的值：

$$ 7（8.58）+ 18（2.86） - 10V_ {3} = 36 $$

展開：

$$60.06 + 51.48 - 10V_ {3} = 36 $$

結合條款：

$$ 111.54 - 10V_ {3} = 36 $$

解決V3：

$$ - 10V_ {3} = -111.54 + 36 $$

將雙方除以-10：

$$ \ underline {V_ {3} = 7.55 \ text {v}} $$

可以使用圖5計算V0的值：

召回：$$ V_ {0} = V_ {1} - V_ {3} $$

替換V1和V3的值：

$$ V_ {0} = 8.58 \ text {v} - 7.55 \ text {v} $$

$$ \ underline {V_ {0} = 1.03 \ text {v}} $$

既然已知所有節點電壓，可以計算電阻器R1（IR1），R2（IR2），R3（IR3）和電阻器的電流R4（IR4）。

召回：$$ I_ {R_ {1}} = \ frac {V_ {2}} {R_ {1}} $$

$$ I_ {R_ {1}} = \ frac {2.86 \ text {v}} {\ text {1 k} \ Omega} $$

$$ \ underline {I_ {R_ {1}} = 2.86 \ text {mA}} $$

召回：$$ I_ {R_ {2}} = \ frac {V_ {2} - V_ {3}} {R_ { 2}} $$

$$ I_ {R_ {2}} = \ frac {2.86 \ text {v} - 7.55 \ text {v}} {\ text {2k} \ Omega} $$

$$ \ underline {I_ {R_ {2}} = -4.69 \ text {v}} $$

$$ \ underline {I_ {R_ {2}} = -2.35 \ text {mA}} $ $

召回：$$ I_ {R_ {3}} = \ frac {V_ {1} - V_ {3}} {R_ {3}} $$

$$ I_ {R_ {3}} = \ frac {8.58 \ text {v} - 7.55 \ text {v}} {\ text {3 k} \ Omega} $$

$$ I_ {R_ {3}} = \ frac {1.03 \ text {v}} {\ text {3 k} \ Omega} $$

$$ \ underline {I_ {R_ {3 }} = 0.34 \ text {mA}} $$

召回：$$ I_ {R_ {4}} = \ frac {V_ {1} - V_ {4} } {R_ {4}} $$

$$ I_ {R_ {4}} = \ frac {8.58 \ text {v} - 4 \ text {v}} {\ text {4 k} \ Omega} $$

$$ I_ {R_ {4}} = \ frac {4.58 \ text {v}} {\ text {4 k} \ Omega} $$

$$ \ underline {I_ {R_ {4}} = 1.15 \ text {mA}} $$

要確認KCL當前計算，請考慮超級節點上關聯的那些：

$$ - I_ {1} + I_ {R_ {1}} + I_ {R_ {2}} + I_ {R_ {3}} + I_ {R_ {4}} = 0 $$

替代電路值：

$$（ - 2 \ text {mA}）+ 2.86 \ text {mA} - 2.35 \ text {mA} + 0.34 \ text {mA} + 1.15 \ text {mA } = 0 $$

結合條款：

$$ 4.35 \ text {mA} - 4.35 \ text {mA} = 0 $$

確認V3節點的KCL當前計算：

$$ - I_ {2} + I_ {R_ {2}} + I_ {R_ {3}} = 0 $$

注意IR2和IR3是超級節點計算的相反符號

$$（ - 2 \ text {mA}）+ 2.35 \ text {mA} - 0.34 \ text {mA} = 0 $$

組合術語：

$$ （-2.34 \ text {mA}）+ 2.35 \ text {mA} \ approx0 $$

電壓控制電流源是輸出電流（IS）是線性的具有以下關系中的參考電壓（VX）的連通組件的功能：

IS =（A）（IX）其中A是乘數，需要確定IX。

VCCS的下圖如圖1所示。

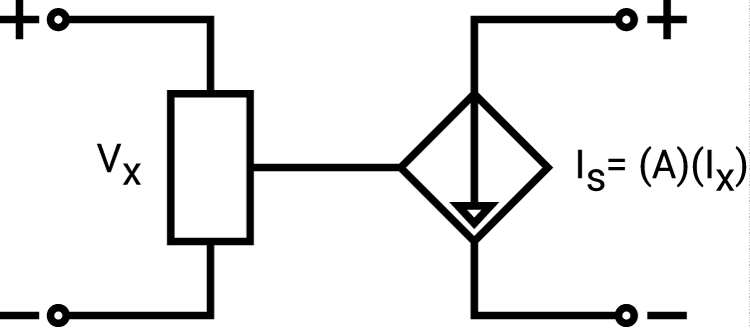
圖1.壓控電流源

考慮以下電路，該電路由依賴電壓源I2組成值（-2mA）（VR1），與電阻R1的連接鏈路，其值為1K歐姆，電壓降為VR1，獨立電壓源V1的值為4伏，獨立電流源I1具有值1 mAmp，如圖2所示。

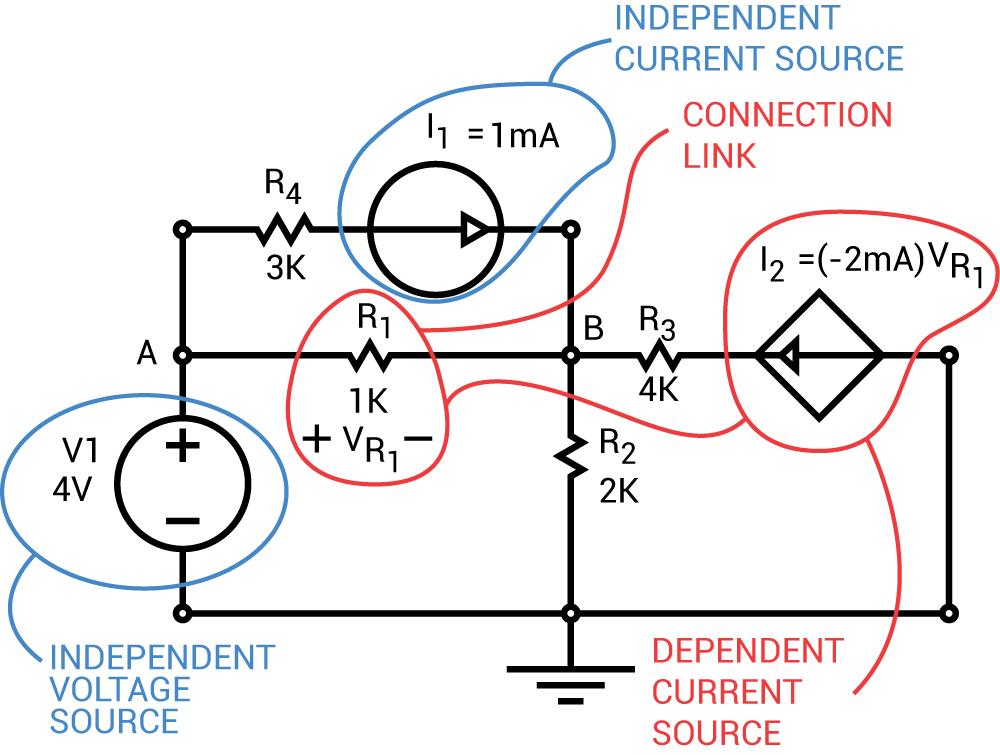
圖2。

在節點B使用基爾霍夫電流定律（KCL）之前，節點A的電壓可以使用4伏的獨立電壓源V1的值來確定：

$$ V_ {A} = V_ {1} = 4 \ text {volts} $$

要確定節點A處的KCL，需要識別電流。電流IA是正的，因為它進入節點而電流IB和IC是負的，因為它們離開節點，如圖3所示。

圖3.

節點VA上所有電流的代數和等于零：

$$ I_ {A} - I_ {B} - I_ {C} = 0 $$

請注意：

$$ I_ {B} = \ frac {V_ {B} - V_ {A}} { R_ {1}} $$

$$ I_ {C} = I_ {1} $$

這樣：

$$ I_ {A} - \ frac {V_ {B} - V_ {A}} {R_ {1}} - I_ {1} = 0 $$

替換電路值：

$$ I_ {A} - \ frac {V_ {B} - 4} {1 \ text {k} \ Omega} - 1 \ text {mA} = 0 $$

將兩邊乘以1k：

$$ [I_ {A} - \ frac {（V_ {B} - 4）} {1 \ text {k} \ Omega} - 1 \ text {mA} = 0]（1 \ text {k} ）$$

展開：

$$（1 \ text {k}）I_ {A} - （V_ {B} - 4） - 1 = 0 $$

$$（1 \ text {k}）I_ {A} - V_ {B} + 4- 1 = 0 $$

組合術語：

$ $（1 \ text {k}）I_ {A} - V_ {B} + 3 = 0 $$

左側未知，右側知道

$$（1 \ text {k}）I_ {A} - V_ {B} = -3 $$ [等式1]

要確定節點B處的KCL，需要識別電流。當前的IA，IB和IC是正的，因為它們進入節點，而當前的IE是負的，因為它離開節點，如圖4所示。

圖4.

節點VB上所有電流的代數和等于零：

$$ I_ {B } + I_ {C} + I_ {D} - I_ {E} = 0 $$

請注意：

$$ I_ {B} = \ frac {V_ {A } -V_ {B}} {R_ {1}} $$

$$ I_ {C} = I_ {1} $$

$$ I_ {D} = I_ {2} $$

$$ I_ {E} = \ frac {V_ {B}} {R_ {2}}

這樣：

$$ \ frac {V_ {A} -V_ {B}} {R_ {1}} + I_ {1} + I_ {2} - \ frac {V_ {B}} {R_ {2}} = 0 $$

替換電路值：

$$ \ frac {4-V_ {B}} {1 \ text {k} \ Omega} + 1 \ text {mA} - （2 \ text {m}）V_ {R_ {1}} - \ frac {V_ {B}} {2 \ text {k} \ Omega} = 0 $$

將兩邊乘以2 k：

$$ [\ frac {4-V_ {B}} {1 \ text {k} \ Omega} + 1 \ text {mA} - （2 \ text {m}）V_ {R_ { 1}} - \ frac {V_ {B}} {2 \ text {k} \ Omega} = 0]（2 \ text {k}）$$

展開：

$$ 2（4 -V_ {B}）+ 2 -4V_ {R_ {1}} -V_ {B} = 0 $$

$$ 8 -2V_ {B} + 2 -4V_ {R_ {1}} -V_ {B} = 0 $$

組合術語：

$$ - 3V_ {B} -4V_ {R_ {1}} + 10 = 0 $$

左邊未知，右邊知道

$$ - 3V_ {B} -4V_ {R_ {1}} = -10 $$ [等式2]

$$ E_ {R_ {4}} = I_ {1} R_ {4} $$

替換電路值：

$$ E_ {R_ {4}} =（1 \ text {mA}）（3 \ text {k} \ Omega）$$

$$ \ underline {E_ {R_ {4}} = 3 \ text {v}} $$

請注意，R4與R1并行。這使得ER4等于VR1。

$$ \ underline {V_ {R_ {1}} = 3 \ text {v}} $$

使用歐姆定律找到IB：

\ [I_ {B} = \ frac {V_ {R1}} {R_ {1}} \]

替換電路值：

$$ I_ {B} = \ frac {3 \ text {v}} {1 \ text {k} \ Omega} $$

$$ \ underline {I_ {B} = 3 \ text {mA}} $$

回憶節點A的電流：

$$ I_ {A} -I_ {B} -I_ {C} = 0 $$

求解IA：

$$ I_ {A} = I_ {B} + I_ {C} $$

替代電路值：

$$ I_ {A} =（3 \ text {mA}）+（1 \ text {mA}）$$

$$ \ underline {I_ {A} = 4 \ text { mA}} $$

請注意，當前ID是當前的I2：

$$ I_ {D} =（ - 2 \ text {m}） （V_ {R_ {1}}）$$

替換電路值：

$$ I_ {D} =（ - 2 \ text {m}）（3 \ text { v}）$$

$$ \ underline {I_ {D} = - 6 \ text {mA}} $$

回憶節點電流B：

$$ I_ {B} + I_ {C} + I_ {D} -I_ {E} = 0 $$

解決IE：

$$ I_ {E} = I_ {B} + I_ {C} + I_ {D} $$

替換電路值：

$$ I_ {E} = （3 \ text {mA}）+（1 \ text {mA}）+（ - 6 \ text {mA}）$$

$$ \ underline {I_ {E} = - 2 \ text {mA}} $$

請注意，VR1可以從節點A和節點B確定：

$$ V_ {R_ {1}} = V_ {A} -V_ {B} $$

解決VB：

$$ V_ {B} = V_ {A} -V_ {R_ {1}} $$

替換電路值：

$$ V_ {B} =（4 \ text {v}） - （3 \ text {v}）$$

$$ \下劃線{V_ {B} = 1 {\ text {v}}} $$

使用與從屬電流源關聯的等式來查找當前的I2：

$$ I_ {2} =（ - 2 \ tex t {m}）（V_ {R_ {1}}）$$

替換電路值：

$$ I_ {2} =（ - 2 \ text {m}）（3 \ text {v}）$$

$$ \下劃線{I_ {2} = - 6 \ text {mA}} $$

使用歐姆定律查找電阻R3上的電壓：

$ $ E_ {R_ {3}} =（I_ {2}）（R_ {3}）$$

替換電路值：

$$ E_ {R_ {3}} =（ - 6 \ text {mA}）（4 \ text {k} \ Omega）$$

$$ \ underline {E_ {R_ {3}} = - 24 \ text {v}} $$

為了確認涉及獨立電壓源V1和電阻器R1和R2的KVL回路，得到以下等式：

$$ V_ {1} = E_ {R_ {1}} + E_ {R_ {2}} $$

替換電路值并注意ER2等于VB

$$（4 \ text {v}） =（3 \ text {v}）+（1 \ text {v}）$$

使用依賴源的節點分析利用Kirchhoff的當代法與代數和歐姆定律來代替節點的未知電壓并找到其他電路值。通過花時間仔細標記節點，通過識別正確的節點電壓和極性，解決問題變得更容易并且可以避免錯誤。