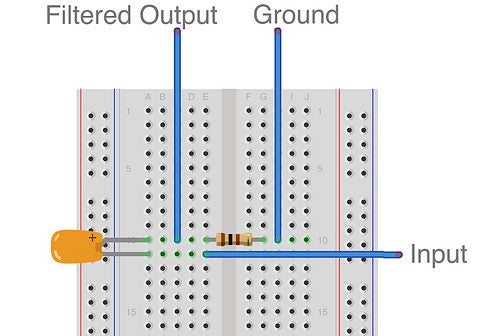
您需要的東西
您要放入電路的東西:
一個電阻為R(在Ω中)。
輸入信號(我們來自函數發生器)。
示波器(用于測試)。
從電路中得到的結果:
經過濾波的輸出信號。
如何構建電路

零件在哪里?
您的輸入信號首先被饋入電容器,該電容器的另一端連接到電阻器,該電阻器的另一端連接到地。您的輸出信號應在電容器和電阻器之間讀取。
進行測試以確保其正常工作。
如果您無法使用函數發生器或示波器,則可以必須相信我們為您正確測試了電路。我們構建了如下所示的電路:
紅色的鱷魚夾夾住了來自函數發生器的輸入信號,黑色的鱷魚夾夾住了地,綠線承載我們的輸出信號,然后將其發送到示波器進行測試。當我們從低頻信號變為高頻信號時,我們在示波器上讀取的結果看起來像這樣:
黃色曲線是我們的輸入信號,藍色曲線是我們的輸出信號(請注意,盡管黃色曲線看起來保持不變,這是因為我們正在改變示波器顯示屏上的頻率縮放比例)。在低頻下,您可以看到整個信號都被濾除,幾乎沒有輸出信號。隨著頻率的增加,輸出信號會變大,直到達到與輸入信號幾乎相同的點為止。這稱為截止頻率,稍后我們將向您展示如何找到它。您還應該注意,輸出信號可以與原始輸入信號相移,這意味著盡管信號具有相同的頻率,但不一定一定是“同步”。
另外,請注意,雖然我們有意一次輸入了一個均勻頻率的信號,但該電路將對復合信號起作用。
截止頻率
計算截止頻率。
截止頻率通常被認為是信號衰減(或濾波)的頻率。這意味著頻率低于截止頻率的任何信號都被視為已濾波,而頻率高于截止頻率的任何信號均被視為“左撇子”或未濾波。那么截止頻率是多少?

其中, R 是電阻的電阻,單位為Ω, C 是電容器的電容,單位是 F 。
信號的截止頻率是什么意思?
如果您看一下在很寬的頻率范圍內輸出信號的幅度與輸入信號的幅度之比,您將得到如下效果

請注意,兩個軸都是對數縮放的。這實際上意味著,如果您從一條淺灰色線向上移動到下一條灰色線,則您的值實際上會增加10倍。這意味著,如果您在沒有對數刻度軸的情況下查看此圖,則實際上會看到截止頻率幾乎垂直下降。但是,頻率高于截止頻率的任何信號或信號成分都未經濾波,可以很好地近似。
輸出信號與輸入信號相移。
前面我們說過,輸入和輸出信號不是“同步”的,而是實際發生了移位。這對于某些應用程序可能很好,但是在其他一些應用程序中這可能很重要。隨著輸入信號頻率的變化,相移也隨增益的變化而變化,并且這種變化的曲線看起來像這樣。

頻率時,輸出信號相移π/2,而在高頻時,相移幾乎為零。截止頻率對于相移很重要,因為它是輸出信號相移恰好是π/2或π/4的一半的頻率。
您如何獲得這些結果? !?!
如果您真的想知道,請查看理論部分,以獲取有關電路工作原理以及我們如何計算增益和相移的更多信息。
TL; DR
高通濾波器可以按以下方式制造:
輸入-電容器-(輸出)-電阻-接地
高通濾波器濾除頻率低于截止頻率(1/2πRC)的信號。
由于截止頻率由R和C嚴格確定,因此請選擇適當的電阻器和電容器來截止您想要的頻率
輸出信號與輸入信號相移。
步驟2:低通濾波器

此部分的內容與“高通濾波器,因此,如果您已經讀過它,那么在那里發現的許多信息也將適用于低通濾波器,除了幾乎所有的東西都翻轉了。
您需要的東西
要放入電路中的東西:
一個電容為C(在 F 中的電容器)。
一個電阻為R(在Ω中)。
輸入信號(我們來自函數發生器)。
示波器(用于測試)。
您將從電路中獲得的收益:
經過濾波的輸出信號。
如何構建電路

零件在哪里?您的輸入信號首先被饋入電阻器,該電阻器的另一端連接到電容器,而電容器的另一端則連接到地。您的輸出信號應該在電阻和電容之間讀取。
進行測試以確保其正常工作。
如果您無法使用函數發生器或示波器,則可以必須相信我們為您正確測試了電路。我們構建了如下所示的電路:
紅色的鱷魚夾夾住了輸入信號(來自函數發生器),黑色的鱷魚夾夾住了地,綠線承載我們的輸出信號,然后將其發送到示波器進行測試。當我們從低頻信號變為高頻信號時,在示波器上讀取的結果如下所示:
黃色曲線是我們的輸入信號,藍色曲線是我們的輸出信號(請注意,盡管黃色曲線看起來保持不變,這是因為我們正在改變示波器顯示屏上的頻率縮放比例)。在低頻下,您會看到幾乎沒有信號被濾波,并且我們的輸出幾乎與我們的輸入相同。當頻率達到截止頻率時,輸出信號開始明顯小于輸入信號。從這里開始,隨著頻率的增加,輸出信號變得越來越小,直到幾乎沒有信號剩下為止。您還應該注意,輸出信號可以與原始輸入信號相移,這意味著盡管信號具有相同的頻率,但不一定一定是“同步”。
另外,請注意,雖然我們有意一次輸入了一個均勻頻率的信號,但該電路將對復合信號起作用。
截止頻率
計算截止頻率。
截止頻率通常被認為是信號衰減(或濾波)的頻率。這意味著,頻率高于截止頻率的任何信號都被視為已濾波,而頻率低于截止頻率的任何信號均被視為“獨立”或未濾波。那么截止頻率是多少?

其中, R 是電阻的電阻,單位為Ω, C 是電容器的電容,單位是 F 。
信號的截止頻率是什么意思?
如果您看一下在很寬的頻率范圍內,輸出信號的幅度與輸入信號的幅度之比,您會得到如下效果

請注意,兩個軸都是對數縮放的。這實際上意味著,如果您從一條淺灰色線向上移動到下一條灰色線,則您的值實際上會增加10倍。這意味著,如果您在沒有對數刻度軸的情況下查看此圖,則實際上會看到截止頻率幾乎垂直下降。但是,頻率低于截止頻率的任何信號或信號成分都未經濾波,可以很好地近似。
輸出信號與輸入信號相移。
前面我們說過,輸入和輸出信號不是“同步”的,而是實際發生了移位。這對于某些應用程序可能很好,但是在其他一些應用程序中這可能很重要。隨著輸入信號頻率的變化,相移也隨增益的變化而變化,并且這種變化的圖看起來像這樣。

在高頻率下,輸出信號相移為零,而在高頻下,相移幾乎為π/2。截止頻率對于相移很重要,因為它是輸出信號相移恰好是π/2或π/4的一半的頻率。
您如何獲得這些結果? !?!
如果您真的想知道,請查看理論部分,以獲取有關電路工作原理以及我們如何計算增益和相移的更多信息。
TL; DR
低通濾波器可按以下方法制造:
輸入-電阻-(輸出)-電容器-接地
低通濾波器濾除頻率超過截止頻率(1/2πRC)的信號。
由于截止頻率由R和C嚴格確定,因此請選擇適當的電阻器和電容器截止頻率。
輸出信號從輸入端移相。
步驟3:帶阻和帶通濾波器

我們將僅簡要討論陷波濾波器和帶通濾波器在這里。這些只是此類過濾器的最基本版本,因此只能滿足最基本的需求。
陷波/陷波/擋帶過濾器
這是什么?
帶阻濾波器是一種電路,可以理想地濾除頻率在一定范圍內的信號。該范圍可能很大,具體取決于電路的固有特性。電路濾波的頻率范圍越小,據說它的 Q 系數就越高。具有高 Q 因子的帶阻濾波器也稱為陷波濾波器。
構建一個簡單的陷波濾波器。
使用電阻器,電容器和電感器,您可以構建一個簡單的陷波濾波器,如下所示:
它可以濾除哪些頻率?
中心頻率,也稱為可以在該電路周圍進行濾波的諧振頻率可以找到

,其中L是 H ,C是 F 中電容器的電容。
帶通濾波器
是什么
帶通濾波器是理想地濾除除特定范圍內的所有頻率之外的所有信號的電路。該范圍可能很大,具體取決于電路的固有特性。電路允許通過的頻率范圍越小,據說它具有的 Q 因子就越高。
構建一個簡單的帶通濾波器。
使用電阻,電容器和電感器,您可以按如下所示構建一個簡單的帶通濾波器:
它允許通過哪些頻率?
可以使電路通過的中心頻率或諧振頻率類似于

,其中L是電感的 H 中的電感,C是 F 中電容器的電容。
步驟4:濾波電路背后的原理
來自xkcd.com的圖像。
此處的此步驟僅是為了沉迷您的科學好奇心和
分壓器
什么是分壓器?
顧名思義,分壓器是吸收電流的電路輸入電壓并輸出等于輸入電壓一部分的輸出電壓。電路本身就是一個電壓源,它與兩個電阻串聯,兩個電阻之間的輸出如下所示。

了解分壓器工作原理的關鍵是知道電流 I 在整個如果在輸出端沒有汲取電流,則兩個電阻器都將輸出。使用歐姆定律( V = IR ,電壓=電流x電阻),我們看到兩個電阻中每個電阻的壓降與電阻成正比。例如,如果電阻具有相同的電阻,則輸入電壓將在兩個電阻之間平均分配。換句話說(實際上得到輸出電壓的公式),讓我們使用歐姆定律根據輸入電壓和總電阻來計算電路的電流。

現在再次使用歐姆定律根據輸出電壓計算電路的電流。

第二個電阻上的壓降為等于輸出電壓。請注意,正如我們之前所說,這兩個電流相等,因此我們可以將兩個方程式設置為相等,并求解輸出電壓。

這表明輸出電壓取決于第二個電阻器的電阻與兩個電阻器的總電阻之比。
一個簡單的例子

電容器的阻抗
您可能已經注意到,我們的高通和低通濾波器只是分壓器,其中一個電阻替換為電容器。因此,我們可以在理論上進行與上述相同的分析,以了解濾波器的工作原理,但是首先我們需要了解阻抗。
您可以將阻抗視為廣義電阻。例如,眾所周知,電阻器的阻抗稱為電阻。電阻器的阻抗僅為R,即電阻值,但是電容器的阻抗是多少?阱電容器的阻抗用復數值1/(jωC)表示,其中C是電容器的電容,ω是通過電容器的信號頻率,以弧度表示(ω=2π f ,其中 f 是頻率(以赫茲為單位),而j只是虛數 i =√-1,(我們使用j代替i,所以我們不會混淆它
注意電容器的阻抗與頻率有關。對于接近零的頻率,電容器的阻抗變為無窮大,但是,對于非常高的頻率,其阻抗變為零。換句話說,電容器的阻抗在低頻下看起來像是一個大電阻,在高頻下就像一條沒有電阻的簡單導線。
了解高通和低通電路
您還記得確定分壓器輸出的方程式

如果將其推廣用于阻抗,我們將得到類似

其中 Z 只是我們電路元件的阻抗,而波浪線或波浪線僅表示我們正在處理復雜的信號數字。對于低通濾波器,我們在頂部有一個電阻,在底部有一個電容,所以

這看起來有點討厭,但是如果我們簡化一下,我們得到

還不錯吧?
最后一個公式是理解為什么低通濾波器僅對高頻進行濾波的關鍵。注意,對于低頻,jωRC近似為零,因此輸出電壓近似等于輸入電壓。現在對于高頻,jωRC近似為無限,因此我們得到輸出電壓幾乎為零。看看這是如何工作的?當我們的復數電壓(由不同頻率的各種波組成)用作濾波器的輸入電壓時,電壓的高頻部分產生的輸出電壓等于零,而低頻部分產生的輸出電壓等于輸入電壓(即我們只獲得信號的低頻部分)。
應用于低通濾波器的相同論點可以用于高通濾波器,只需切換電阻器和電容器的位置。我們仍然使用相同的公式

但是,這次

如果我們簡化,我們應該再次得到

對于高頻,我們基本上得到jωRC≈jωRC+ 1,所以我們應該得到一個等于輸入的輸出電壓電壓。對于低頻,我們得到jωRC≈0,因此輸出電壓幾乎為零。如您所見,正如我們所承諾的那樣,我們跳過了高頻,只濾出了低頻。
截止頻率
如前所述,截止頻率對于高通或低通濾波器電路,要知道一個非常重要的值。我們實際上如何找到它呢?截止頻率定義為輸出電壓精確等于輸入電壓的1/√2的頻率。這是濾波器開始衰減輸入信號的點。如果使用上面的方程式求解該頻率,則會發現

,其中ω=2π f 。如您所見,截止頻率嚴格取決于我們為電阻和電容選擇的值,因此我們可以準確選擇希望電路開始過濾信號的位置。
責任編輯:wv
-
濾波器電路
+關注
關注
2文章
75瀏覽量
24495
發布評論請先 登錄
相關推薦
無源濾波器的影響因素
LC濾波器和RC濾波器有哪些差異
高通濾波器電路屬于直流電路嗎
emi濾波器是什么濾波器
iir濾波器和fir濾波器的優勢和特點
高通濾波器和低通濾波器判別方法
有源濾波器和無源濾波器的原理及區別是什么
低通濾波器電路圖分享




 如何制作多種不同的濾波器電路
如何制作多種不同的濾波器電路











評論