步驟1：了解算法第1部分：定積分及其使用

我假設您對基本演算的背景了解一點積分。積分很重要，因為它們使您可以將值數組乘以 infinitesimal 長度求和；這在金融，數論，物理，化學以及許多其他領域中很有用。但是，該程序僅允許您計算有限間隔內曲線下方的面積，換句話說，它不會評估反導數-要使用更強大的算法，那。如果您需要在針對其他對象指定的較大程序中求值定積分，或者要檢查答案是否需要手工完成，則此算法很有用。

基本定積分表示函數定義的曲線下的面積，例如F（X）。對于確定的積分，我們求兩點之間的面積（分別標記為a和b）。在圖片中，綠松石區域是我所指的區域，并且確定該區域的公式也顯示在該區域中。圖片中顯示的功能是任意的。

步驟2：了解算法第2部分：數值逼近

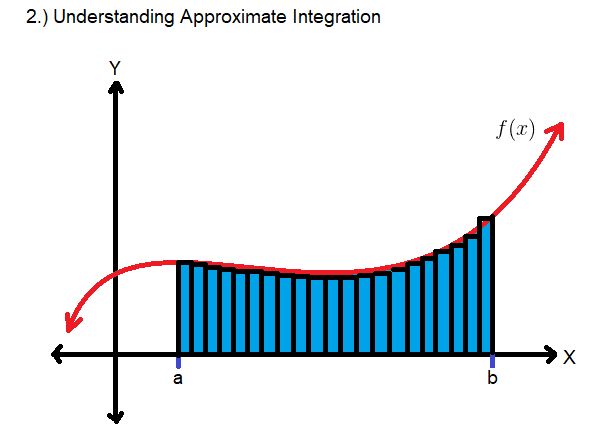
計算機需要大量的指令來計算該面積在可用于任何功能的任意函數下，因此您可能熟悉的分析方法沒有用，因為它們太特殊了。一種計算機可以實際處理的近似計算積分的方法是，用感興趣的區域填充用戶定義的寬度和高度可變的矩形，然后對所有矩形區域求和，從而完成計算。矩形的剛性將使某些總面積保持不變，因此為什么將其視為近似值；但是，您可以在邊界（a和b）之間填充的矩形越多，由于未觸摸的區域變得稀疏，所以近似值越準確。由于計算機將執行此任務，因此可以將所需區域中的矩形數量設置為非常大的數量，從而使逼近非常精確。在支持圖片中，假設指定區域中的每個矩形都具有相等的寬度。我盡了最大努力使它們在Microsoft Paint中具有相等的寬度，但沒有做得最好。

步驟3：了解算法第3部分：中點規則

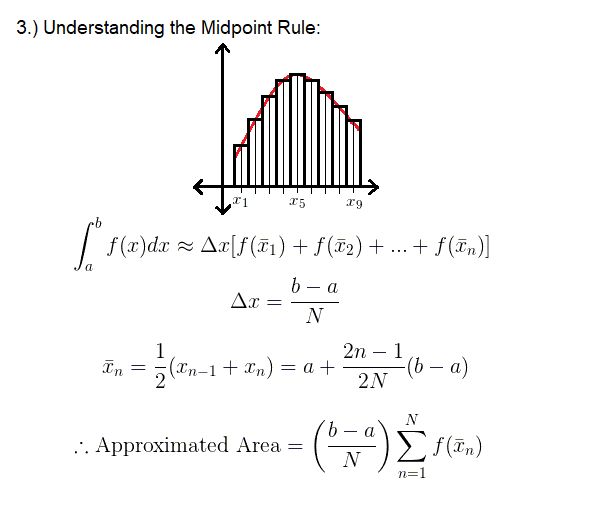
此規則指定如何在矩形中制作和使用矩形近似值。 “ N個”矩形中的每個矩形必須具有相等的寬度Δx，但每個第n個矩形不能完全相同：變化因子是高度，它隨在某個點求值的函數而變化。中點規則之所以得名，是因為您將每個矩形的高度評估為f（x_n），其中“ x_n”是每個矩形的相應中心點，分別位于矩形的左側或右側。使用中點就像實現平均值，比起使用右或左時，將使近似值更準確。此步驟的輔助圖片總結了如何在數學上定義中點規則。

第4步：創建程序第1部分：下載Python編譯器/編輯器

現在，您了解了需要實現的算法，即讓計算機為您執行計算的問題。告訴計算機該怎么做的第一步是獲取執行此操作的工具。該算法可以用任何語言編碼。為簡單起見，該程序將使用Python語言進行編碼。要命令您的計算機執行Python操作，您將需要一個編輯器，該編輯器以該語言編寫指令，然后將其編譯為計算機可以理解的機器語言，從而可以執行您要執行的任務。在當今時代，通常將編輯器和編譯器集成在一起，但是并不總是如此。您可以使用任何您喜歡的編輯器/編譯器，但我將向您展示如何獲取我個人最喜歡的Python：Canopy。如果您已經具有編輯器/編譯器，則可以跳過這些步驟。

轉到https://www.enthought.com/product/canopy/

單擊下載機蓋

單擊與您的操作系統相對應的下載按鈕

下載將自動開始。

啟動后，請按照滴注說明進行操作執行文件

運行程序

從程序主菜單中單擊“編輯器”

在屏幕中央單擊“創建新文件”

從這一點開始，您應該看到一個空白的白色窗口，其光標類似于基本的文字處理文檔。現在您可以開始編碼用于求解定積分的數值積分算法了。后續步驟將提供您要復制的代碼片段，并說明該代碼片段對整個程序的作用。

步驟5：創建程序第2部分：導入函數和定義變量

將代碼復制到圖片中。

對于您可能會發現自己進行編碼的任何程序，都會有變量。變量是給將要操作并且可以更改的值的名稱。在大多數編程語言（如果不是全部）中，您必須先初始化變量，然后程序才能對其進行更改。在此程序中，我將變量命名為“ N”，“ a”和“ b”。這些值分別表示迭代數（矩形的AKA數），下邊界和上邊界。您可以隨意命名這些名稱，但要匹配“理解算法第3部分：中點規則”中給出的公式，最好使其保持不變。請注意，它們不僅設置為特定值。這是因為將它們作為輸入，以便在運行程序時，程序的用戶可以定義值。輸入命令后，引號中的文字會在您運行程序時顯示，告訴您要鍵入哪種類型的值。您還將注意到，在輸入名稱之前使用了“ int”和“ float”。這些術語告訴計算機此值將是什么類型的變量。 “ int”是整數，“ float”是浮點值（即十進制）。應該清楚為什么要這樣指定它們。

在“＃”之后出現的任何文本都是注釋，它使程序員可以以人性化的方式遵循代碼；我已經在您的代碼中做了一些注釋，您將復制這些注釋，但是可以隨意添加任何對您有幫助的注釋。該程序將不會讀取任何帶有“＃”作為命令的內容。

讀取“ from math import *”的代碼部分告訴程序導入一系列可以使用的數學函數無需自己編寫程序。 “ *”僅表示“全部”。將這部分代碼讀為：從數學庫中導入所有函數。這使您可以使用數學函數，例如正弦，余弦，對數，exp等。這些函數可以數學方式集成在代碼中。

第6步：創建程序第3部分：創建集成函數

將代碼復制到前一個下方的圖片中碼。

警告：本部分內容繁瑣，我想清除一些可能引起混淆的內容。在談論編程時，“功能”一詞會彈出很多。當您談論數學時，這個詞也會彈出很多。因此，從這一點開始，當我在編程意義上談論一個函數時，我將寫“ Python函數”，而當我談論數學函數時，我將說“數學函數”。在某些時候，我們將使用Python函數作為所討論數學函數的表示形式。

下一段代碼是程序的核心。在這里，定義了一個Python函數，該函數使用中點規則執行數值積分算法。 “ def Integrate（N，a，b）”的讀法是：定義一個名為“ Integrate”的函數，該函數接受變量“ N”，“ a”和“ b”，并返回曲線下方的面積（數學函數）這也在“集成” Python函數中定義。您可以在進行編碼時以任何方式調用此Python函數，但是將其稱為集成是有意義的，因為它確實集成了數學函數。

在這一點上，值得一提的是Python隔離代碼塊。代碼塊是執行特定任務的整個部分。不同的編程語言將具有指定的方式來區分這些“塊”。對于Python，一個塊通過縮進來區分：每個執行任務的部分都有自己的縮進，并且其他縮進塊中也可以有縮進塊。這代表了任務中的任務，并從根本上告訴了代碼執行的順序。對于已定義的Python函數“集成”，該函數中的所有內容都縮進一個塊，從而區分將在該函數中執行的任務。這個Python函數中的縮進部分也執行自己的任務。內容如下：列出命令（任務），在命令后面加冒號，并在其下方縮進該命令的內容。

在定義“集成” Python函數之后，您將立即定義另一個稱為f（x）的Python函數。這表示將要積分的數學函數。對于要集成的每個不同的數學函數，您都必須轉到此程序行以對其進行更改（與運行程序時定義的變量不同）。每個Python函數都會有一個返回值，這就是當您將其賦值時該函數返回的結果。在這種情況下，拋出的值是“ x”，而這個“ x”項將采用您拋出的值的值，它是一個臨時值。

接下來，是一個for循環充當本教程“理解算法”部分的公式中定義的求和。此求和需要更多幾個變量，其中一個將作為整個“ Integrate” Python函數的返回值。在for循環之前，我已將這些變量指定為“ value”和“ value2”。 for循環的任務是遍歷指定變量的值范圍，該變量可以在for-loop命令中方便地定義；在這種情況下，該變量為“ n”。發生迭代的范圍是1到N + 1。您應該注意到，上述公式中定義的總和范圍僅從1到N。我們用這種方式進行定義，因為Python語言會從0開始對每個迭代值進行計數，因此我們必須從本質上轉移這些值的范圍以適應我們的期望范圍。然后，for循環允許將所有矩形的高度加在一起，并將該值存儲到我稱為“值”的變量中。這在顯示為：value + = f（a +（（n-（1/2））*（（b-a）/N）））的代碼段中可以看到。

從那里開始，下一段代碼使用名為“ value2”的變量，然后將其分配為每個矩形的所有高度的總和乘以每個矩形的標準化寬度。是我們要在程序中顯示的最終答案，因此是“集成” Python函數的返回值。

第7步：創建程序第4部分：顯示答案

將代碼復制到先前代碼下方的圖片中。

現在，可以通過“集成” Python函數獲得答案了，我們希望能夠顯示它。這只是將用戶輸入的值（“ N”，“ a”和“ b”）放入“集成” Python函數并將其打印在屏幕上的問題。該命令顯示在第21行，它實際上是完成該步驟所需的全部操作。第19和20行上的代碼僅用于“修飾”整個程序的輸出。 “ print（” 。..。..。..。..。..。..。..。..。..。..。..。..。“）”將程序的輸入部分與輸出部分分開，然后“ print （“這是您的答案：”），僅表示將在該行文本之后打印答案。

步驟8：運行程序第1部分：按原樣運行程序

如果您不使用Canopy，則您甚至可能根本不需要執行此步驟，并且運行該程序可能需要不同的過程。在Canopy中，您必須先保存它，然后才能運行該程序。 Python程序的文件類型是.py文件-它會自動保存為。選擇要保存文件的位置，然后就可以運行該程序了。

運行程序：

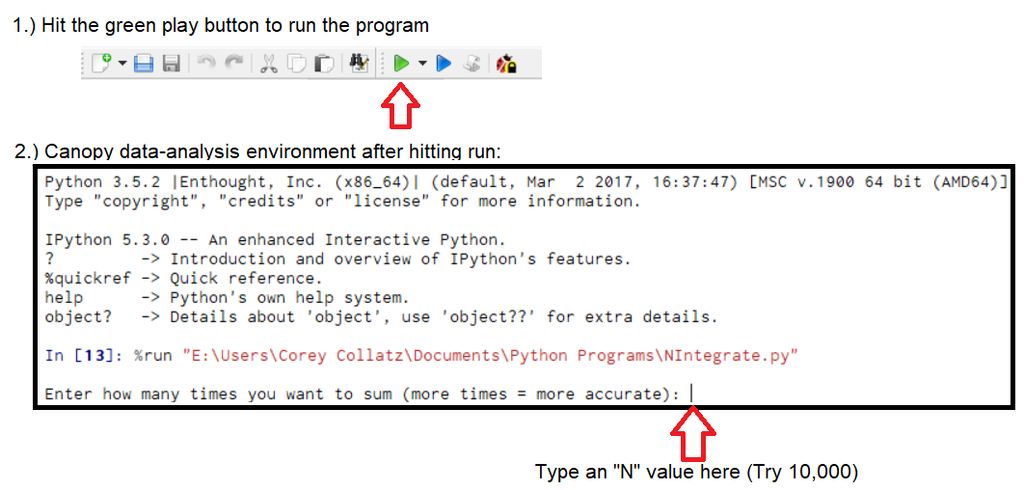
在顯示文件名的工具欄上方，點擊看起來像“播放按鈕”的綠色按鈕（請參閱圖片） ）。

然后該程序將在稱為Canopy數據分析環境的編輯器的底部屏幕中運行。假設您復制了我編寫的提示，則應該在Canopy數據分析環境的底部看到提示：“輸入要累加的次數（更多=更準確）：。”。 （請參閱圖片）

輸入一個值，表示要執行多少次迭代，即10000（要推入您所在區域的矩形數），然后按Enter鍵。

將出現更多的提示，這些提示應該是您在步驟5中編碼到程序中的熟悉的輸入提示。

應該對積分求值，并且應該顯示結果。

如果您如上圖所示對程序進行編碼，則您剛剛積分了f（x） = x ^ 2在一定范圍內。 x ^ 2的積分很容易手動計算，因此您應該檢查并確保程序對手動確定的正確分析值給出了非常接近的答案。當我使用N = 10000，a = 0和b = 10的值運行程序時，得到的答案是333.33333249999964。正確的分析答案是333.333。這是非常準確和快速的。實際上，您已經在x軸上擠壓了10，000個介于0和10之間的矩形，并使用它們來近似計算曲線x ^ 2下的面積！

步驟9：運行程序第2部分：集成其他數學函數

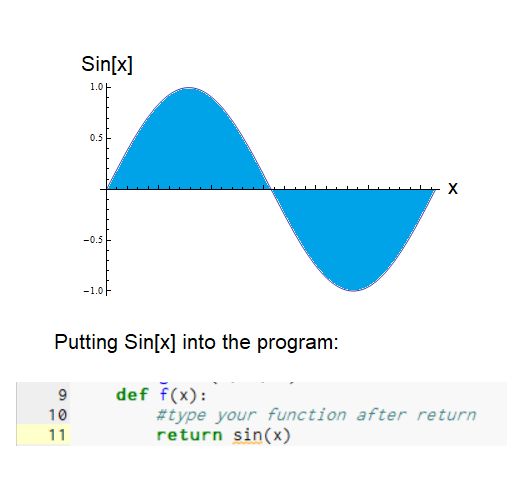
在上一步中，如果您一直在關注忠實地，您對f（x）= x ^ 2進行了積分。這不是該程序可以集成的唯一數學函數。在第5步中，您已經將Python函數的數學庫數組導入程序中。這使您可以使用可以集成的更復雜的數學函數。讓我們試一試。當然，您可以使用任何想要的函數，但是我將通過集成一個特定的數學函數來進一步證明該代碼的準確性，該數學函數在一定范圍內集成時會產生一個眾所周知的值。該函數為f（x）= Sin ［x］。此數學函數顯示在第一張隨附的圖片中，從0到2π進行繪制，并且感興趣的區域以綠松石陰影顯示。在此間隔中，正面積與負面積相等，因此，如果將總面積相加，則應該為零。讓我們看看這是否真的發生：

將數學函數f（x）= Sin ［x］放入程序中：

再次運行程序之前，在注釋下“返回后#type您的函數，”鍵入：sin（x）當前位于x ** 2的位置。 （參考圖片）。

再次點擊綠色的播放按鈕運行程序。

輸入10000作為N值（您希望求和多少次）。

輸入“ 0”作為下邊界。

將6.2832輸入上邊界（大約2π）。

看看您能得到什么價值。

當我這樣做時，最終得到的價值是1.079e-10：這等于.0000000001079，這實際上是接近于零，因此它看起來確實是準確的，并且表明該算法足以處理負區域。

步驟10：運行程序第3部分：擴展程序

至此，您已經完成：您已經在其中編寫了一個有效的確定積分算法可以平穩運行并給出非常準確答案的Python。但是，可以改進此程序。我不是程序員，并且對Python的經驗很少。實際上，我不得不重新學習如何使用Python來完成本教程，但這應該使您相信Python是一種易于學習的語言。我的觀點是，您可以通過提高程序效率來擴展該程序，也許可以實現一些GUI，并使其更加用戶友好。

我對擴展程序的想法：

實現一個圖形用戶界面，使您無需使用Canopy交互式數據分析環境即可運行程序

對其進行設置，以使無需集成要集成的數學函數程序，但可以在程序運行后輸入（我最初是想這樣做，但無法弄清楚）。

定義一個“集成” Python函數，以便將f（x）函數視為在其中定義了f（x）函數的地方。

這些是只是一些需要改進的例子，但我保證還有很多其他可以改進的地方。因此，我將這一步驟作為該程序存在缺陷的一個示例，并作為任何想進一步改進該程序的人的練習。
責任編輯：wv