從今天開始,公眾號陸陸續(xù)續(xù)開始插寫用動(dòng)畫形式展現(xiàn)算法題,如劍指offer、Leedcode里經(jīng)典面試題型,同時(shí)也會(huì)更新數(shù)據(jù)結(jié)構(gòu)與算法基礎(chǔ)、網(wǎng)絡(luò)原理等知識(shí)。
以為無論是面試還是實(shí)際項(xiàng)目,對算法的要求也非常的嚴(yán)格,所以小鹿盡最大努力把算法還原成動(dòng)畫形式來講解,爭取讓每個(gè)人都能看懂算法、學(xué)會(huì)算法。
1
題目
已知前序遍歷為{1,2,4,7,3,5,6,8},中序遍歷為{4,7,2,1,5,3,8,6},它的二叉樹是怎么樣的?
2
基礎(chǔ)鞏固
根據(jù)上述題目所述,我們已知前序遍歷和中序遍歷,回顧一下,什么是前序遍歷?什么是中序遍歷?
2.1 前序遍歷
前序遍歷一顆二叉樹,首先輸出根節(jié)點(diǎn),然后輸出左子節(jié)點(diǎn),最后輸出右子節(jié)點(diǎn)。
比如,遍歷一下二叉樹:
顏色變深表示遍歷,突出表示輸出
2.2 中序遍歷
中序遍歷一棵二叉樹,首先輸出左子節(jié)點(diǎn),然后輸出輸出根節(jié)點(diǎn),最后右子節(jié)點(diǎn)。
以上邊二叉樹為例,通過中序遍歷輸出。
3
解題思路
既然我們知道了二叉樹如何進(jìn)行前序遍歷和中序遍歷了,那么已知前序遍歷和中序遍歷如何反推二叉樹呢?
那么問題來了,只知道前序遍歷能不能反推二叉樹呢?我們就試一下,比如題目中所述,{1,2,4,7,3,5,6,8},根據(jù)前序遍歷,根、左、右,1 肯定是 根節(jié)點(diǎn),那么一下2,4,7.....哪些是左子節(jié)點(diǎn)呢?左子節(jié)點(diǎn)有幾個(gè)呢?很顯然我們是不知道的,由此可以得出,只知道前序遍歷是不可能反推出二叉樹的,中序遍歷也是如此,自己可以嘗試一下。
那么前序遍歷和中序遍歷可不可以?那我們要試一下,我們上邊通過前序遍歷找到第一個(gè)根節(jié)點(diǎn)就是 1,如圖
中序遍歷{4,7,2,1,5,3,8,6}的規(guī)律又是左、根、右,所以 1 結(jié)點(diǎn)在中序遍歷中為根,它的左邊就是所有左子節(jié)點(diǎn)4,7,2,右邊為所有的右子節(jié)點(diǎn)5,3,8,6。
此時(shí)我們已經(jīng)劃分左右子節(jié)點(diǎn)了,但是左邊的子節(jié)點(diǎn)中哪些又是根節(jié)點(diǎn)呢?我們再回到前序遍歷中,根據(jù)前序遍歷的特點(diǎn),根、左、右,在從子節(jié)點(diǎn)進(jìn)行劃分,那么 1 結(jié)點(diǎn)中的子節(jié)點(diǎn)誰為根節(jié)點(diǎn)呢?
我們一眼就能看出來,就是 2 結(jié)點(diǎn),那么剩余的 4,7 左右結(jié)點(diǎn)怎么分呢?我們根據(jù)上述再回到中序遍歷,找到 2 根節(jié)點(diǎn),根據(jù)中序遍歷左、根、右的特點(diǎn),找到 2 結(jié)點(diǎn),那左邊的就是左子節(jié)點(diǎn),右邊的就是右子節(jié)點(diǎn),我們可以看到,左邊有兩個(gè)數(shù),正是 4 和 7 結(jié)點(diǎn)。
右邊只有 1 結(jié)點(diǎn),1 結(jié)點(diǎn)我們剛剛說了,是根節(jié)點(diǎn),所以以 2 為根節(jié)點(diǎn)是沒有右子節(jié)點(diǎn)的,剩下的數(shù)字也是同樣的方式區(qū)分,自己可以試一下,動(dòng)手畫一畫。
我們仔細(xì)發(fā)現(xiàn),其實(shí)整個(gè)層層往下,以及左右,都是相同的解決方式,而且大問題可以分解為小問題,我們下意識(shí)就應(yīng)該想起小鹿之前分享過的知識(shí),那就是遞歸,既然是遞歸,就應(yīng)該有終止條件,終止條件就是當(dāng)子節(jié)點(diǎn)為空時(shí),此時(shí)遞歸結(jié)束。
4
測試用例
我們之前的文章強(qiáng)調(diào)過,手寫代碼之前,一定先把測試用例想好,為了能夠在手寫代碼的時(shí)候考慮到邊界情況,還為了防止你到時(shí)候面試涂涂改改。
4.1 普通測試
完全二叉樹、非完全二叉樹。
4.2 特殊測試
只有左子節(jié)點(diǎn)二叉樹,只有右子節(jié)點(diǎn)、只有一個(gè)結(jié)點(diǎn)的二叉樹 —— 特殊二叉樹測試。
4.3 輸入測試
空樹、空指針null、前序和中序不匹配。
5
代碼實(shí)現(xiàn)
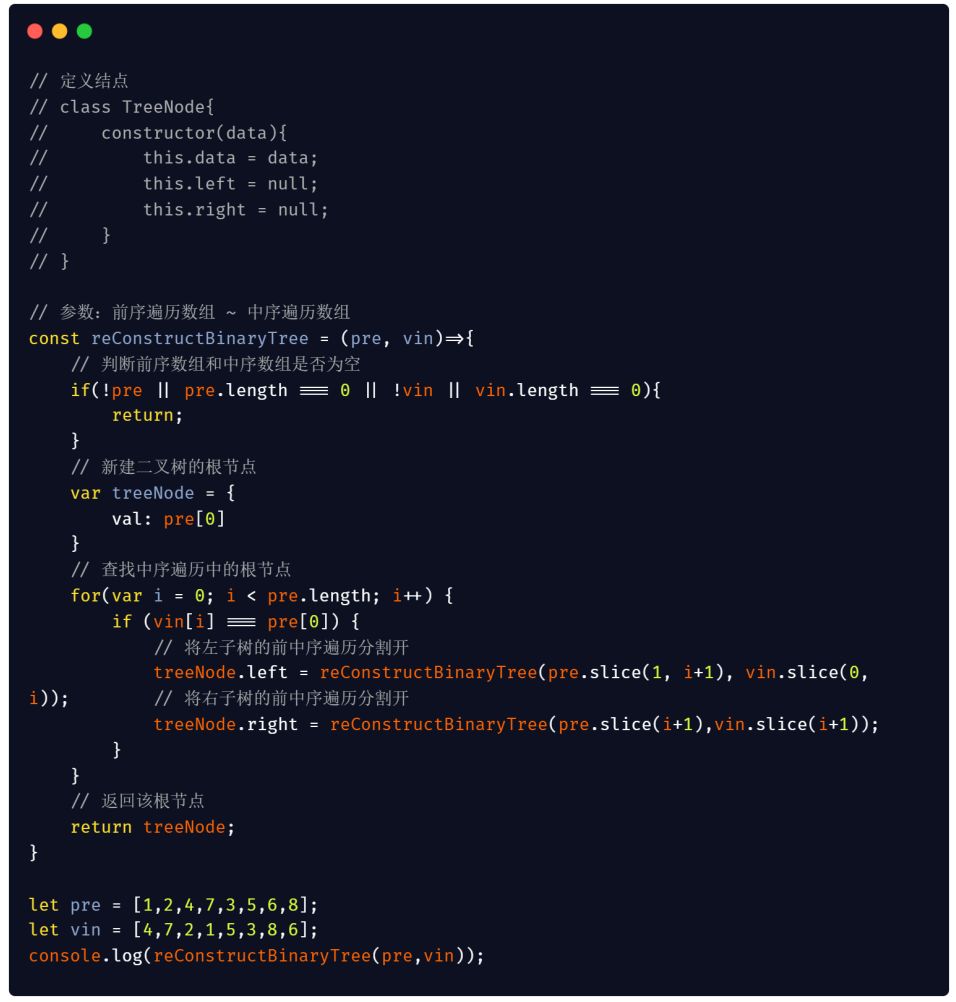
JavaScript 版本
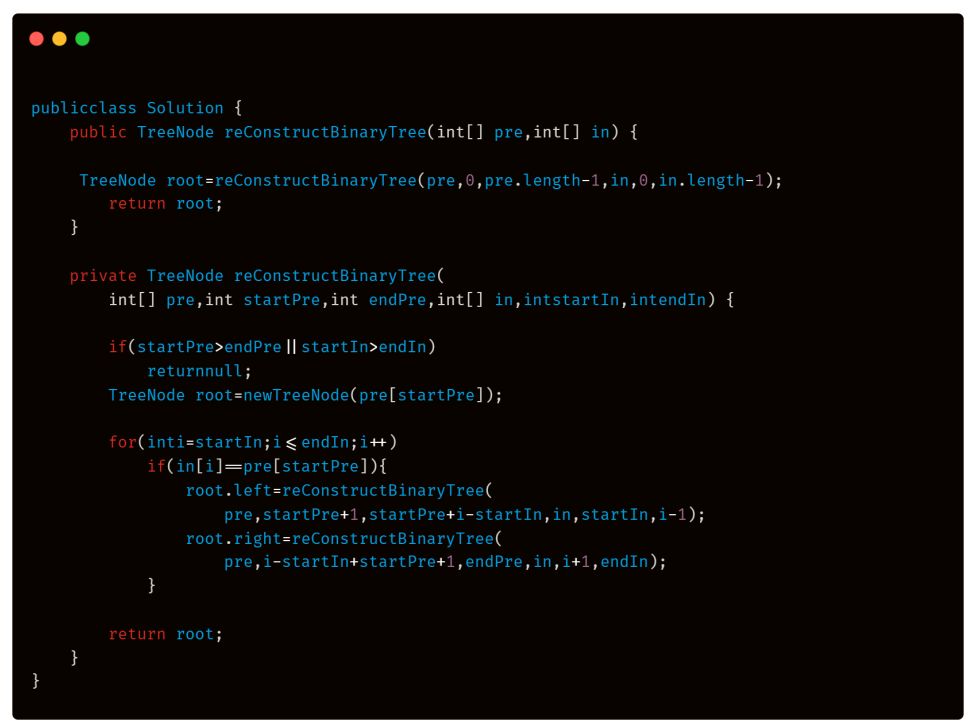
Java 版本
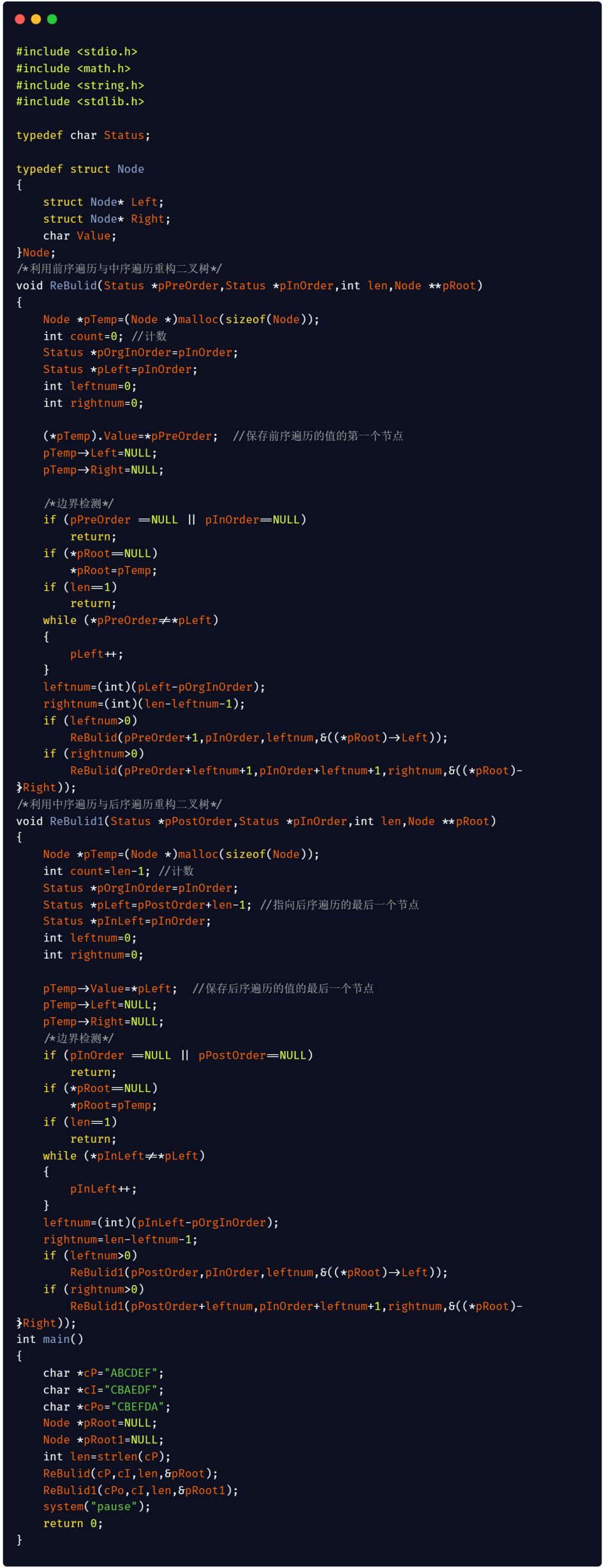
C 語言版本
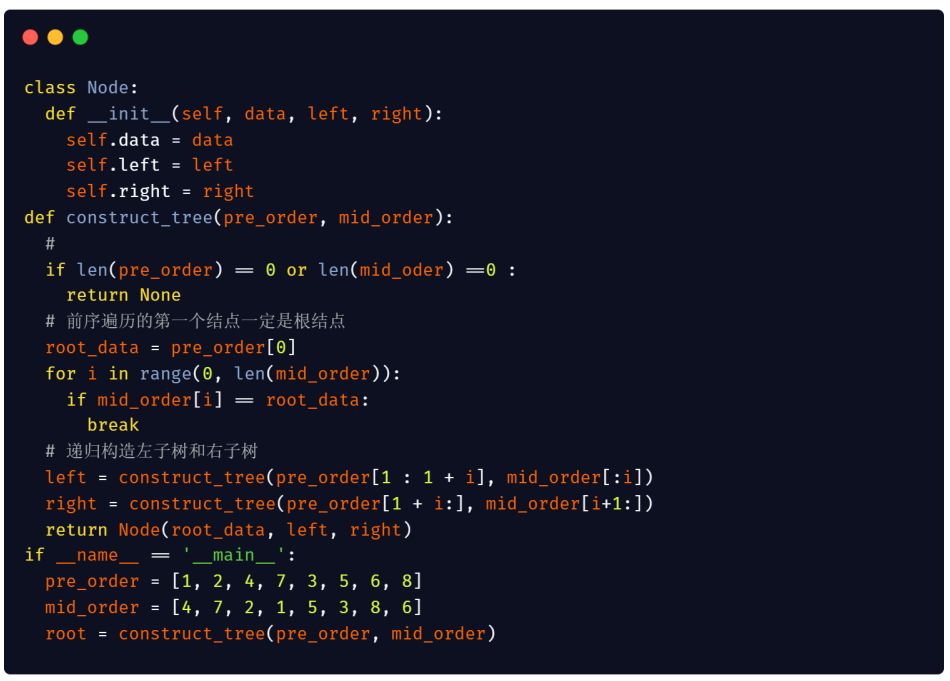
Python 版本
-
算法
+關(guān)注
關(guān)注
23文章
4622瀏覽量
93063 -
二叉樹
+關(guān)注
關(guān)注
0文章
74瀏覽量
12350
原文標(biāo)題:動(dòng)畫:面試算法之重建二叉樹
文章出處:【微信號:TheAlgorithm,微信公眾號:算法與數(shù)據(jù)結(jié)構(gòu)】歡迎添加關(guān)注!文章轉(zhuǎn)載請注明出處。
發(fā)布評論請先 登錄
相關(guān)推薦
嵌入式學(xué)習(xí)-飛凌嵌入式ElfBoard ELF 1板卡-初識(shí)設(shè)備樹之設(shè)備樹組成和結(jié)構(gòu)
飛凌嵌入式ElfBoard ELF 1板卡-初識(shí)設(shè)備樹之設(shè)備樹組成和結(jié)構(gòu)
【面試題】人工智能工程師高頻面試題匯總:機(jī)器學(xué)習(xí)深化篇(題目+答案)
【面試題】人工智能工程師高頻面試題匯總:Transformer篇(題目+答案)
人工智能工程師高頻面試題匯總——機(jī)器學(xué)習(xí)篇

面試嵌入式都會(huì)問那些問題呢?

程序員去面試只需一個(gè)技能征服所有面試官!

什么是默克爾樹(Merkle Tree)?如何計(jì)算默克爾根?
面試嵌入式工作,會(huì)被問什么問題?

叉指電極上覆蓋敏感材料的阻值計(jì)算
多叉指MOSFET器件靜電防護(hù)魯棒性提升技巧
原理圖設(shè)計(jì)里兩顆重要的樹(國產(chǎn)EDA)
康謀分享 | aiSim5仿真場景重建感知置信度評估(三)





 面試算法之重建二叉樹
面試算法之重建二叉樹











評論