在數(shù)字電路中，出于應用的需要，我們可以使用無符號數(shù)，即包括0及整數(shù)的集合；也可以使用有符號數(shù)，即包括0和正負數(shù)的集合。在更加復雜的系統(tǒng)中，也許這兩種類型的數(shù)，我們都會用到。

有符號數(shù)通常以2的補碼形式來表示。圖1列出了4位二進制表示法所對應正負數(shù)。進一步觀察，我們發(fā)現(xiàn)兩種類型數(shù)的加減法是一樣的，做加法和減法就是 在數(shù)輪上按正時鐘轉轉或按反時鐘轉。比方說，1001+0100，意味著從1001按照順時鐘方向移動4個位置，其結果為1101。在無符號數(shù)類型中，它 代表（+9）+（+4）=+13；而在有符號數(shù)類型中，它則代表（-7）+（+4）=-3。從數(shù)輪上看，若是加法所得的結果溢出了，那么也就是穿越了數(shù)輪 的臨界點。注意這個臨界點對于無符號數(shù)和有符號數(shù)來說，是不一樣的：無符號數(shù)，是介于1111和0000之間；有符號數(shù)，則是介于0111和1000之 間。

物理加減法的行為正好和數(shù)輪的移動類似。只要所有的運算子和結果具有相同的位寬，那么有符號數(shù)或無符號數(shù)的形式就可用于相同的電路。比方說，設a、b和sum都是8位信號，表達式

sum = a+ b;

無論這些信號被轉譯成有符號數(shù)或無符號數(shù)，它都會引用相同的硬件且使用相同的二進制表示法。這種現(xiàn)象在其他算術運算中也是正確的（但是它不可用于非算術運算中，比方說有理數(shù)運算或溢出標志位的生成）。

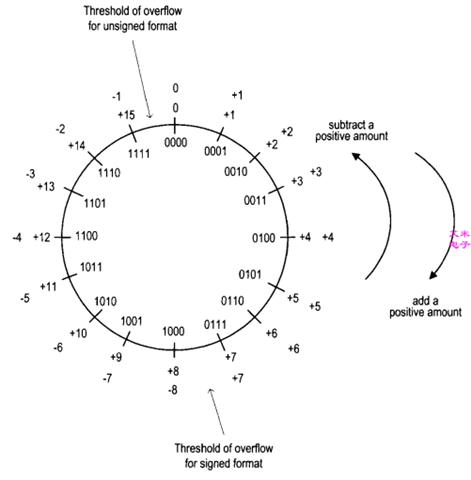
圖1 4位二進制數(shù)輪

此外，當運算子或其結果的位寬不同時，我們需要區(qū)分它究竟使用哪一種符號類型。因為不同的符號類型需要不同的擴展位。對于無符號數(shù)，前置一個0，即 所謂的零擴展位；對于有符號數(shù)來說，需要前置n個所謂的符號擴展位。比方說4位二進制表示的-5為1011；當其擴展成8位時，應該變?yōu)?1111_1011，而不是0000_1011。

舉個例子，設a和sum為8位信號，b為4位信號即b3b2b1b0。

表達式：sum = a + b

需要將b擴展為8位。如果是無符號數(shù)形式，那么b擴展為0000_b3b2b1b0；如果是有符號數(shù)形式，那么b擴展為 b3b3b3b3_b3b2b1b0。上述表達式所引用的硬件包括位寬擴展電路和加法器。因為對于有符號數(shù)和無符號數(shù)來說，擴展電路是不同的；所以上面那 個表達式，對應有符號數(shù)和無符號數(shù)形式，要使用不同的硬件實現(xiàn)。

Verilog-1995中的有符號數(shù)

在Verilog-1995中，只有integer數(shù)據(jù)類型被轉移成有符號數(shù)，而reg和wire數(shù)據(jù)類型則被轉移成無符號數(shù)。由于integer 類型有固定的32位寬，因此它不太靈活。我們通常使用手動加上擴展位來實現(xiàn)有符號數(shù)運算。

下面的代碼片段將描述有符號數(shù)和無符號數(shù)的運算：

01 reg ［7:0］ a， b;

02 reg ［3:0］ c，

03 reg ［7:0］ sum1， sum2， sum3， sum4;

04 。 . 。

05 // same width. can be applied to signed and unsigned

06 sum1 = a + b;

07 // automatica 0 extension

08 sum2 = a + c;

09 // manual 0 extension

10 sum3 = a + {4{ 1‘b0 }， c};

11 // manual sign extension

12 sum4 = a + {4{c［3］}， c};

在第一條語句中，a、b和sum1有相同的位寬，因此無論是轉譯成有符號數(shù)還是無符號數(shù)，它都將引用相同的加法器電路。

在第二條語句中，c的位寬僅為4，在加法運算中，它的位寬會被調整。因為reg類型被作為無符號數(shù)看待，所以c的前面會被自動置入0擴展位。

在第三條語句中，我們給c手動前置4個0，以實現(xiàn)和第二個表達式一樣的效果。

在第四條語句中，我們需要把變量轉譯成有符號數(shù)。為了實現(xiàn)所需的行為，c必須擴展符號位到8位。沒有其他的辦法，只好手動擴展。在代碼中，我們重復復制c的最高位4次（4{c［3］}）來創(chuàng)建具有擴展符號位的8位數(shù)。

Verilog-2001中的有符號數(shù)

在Verilog-2001中，有符號形式也被擴展到reg和wire數(shù)據(jù)類型中。哈哈，新加一個關鍵字，signed，可以按照下面的方式定義：

reg signed ［7:0］ a， b;

使用有符號數(shù)據(jù)類型， 第2節(jié)所述代碼可以被改寫為：

1 reg signed ［7:0］ a， b;

2 reg signed ［3:0］ c;

3 reg signed ［7:0］ sum1， sum4;

4 。 . 。

5 // same width. can be applied to signed and unsigned

6 sum1 = a + b;

7 // automatic sign extension

8 sum4 = a + c;

第一條語句將引用一個常規(guī)的加法器，因為a、b和sum1具有相同的位寬。

第二條語句，所有的右手邊變量都具有signed數(shù)據(jù)類型，c被自動擴展符號位到8位。因此，無需再手動添加符號位。

在小型的數(shù)字系統(tǒng)中，我們通常可以選用有符號數(shù)或者無符號數(shù)。然而，在一些大型的系統(tǒng)中，會包括不同形式的子系統(tǒng)。Verilog是一種弱類型語 言，無符合變量和有符號變量可以在同一表達式中混用。根據(jù)Verilof的標準，只有當所有右手邊的變量具有signed數(shù)據(jù)類型屬性的時候，擴展符號位 才被執(zhí)行。否則，所有的變量都只擴展0。

考慮下面的代碼片段：

1 reg signed ［7:0］ a， sum;

2 reg signed ［3:0］ b;

3 reg ［3:0］ c;

4 。 . 。

5 sum = a + b + c;

由于c不具有signed數(shù)據(jù)類型屬性，因此右手邊的變量b和c的擴展位為0。

Verilog有兩個系統(tǒng)函數(shù)，$signed和$unsigned（），用以將括號內的表達式轉換為signed和unsigned數(shù)據(jù)類型。比方說，我們可以轉換c的數(shù)據(jù)類型，

sum = a + b + $signed（c）;

現(xiàn)在，右手邊的所有變量都具有signed數(shù)據(jù)類型屬性，因此b和c將擴展符號位。

在復雜的表達式中，混用signed和unsigned數(shù)據(jù)類型將引入一些微妙的錯誤，因此應當避免混用。如果真的很有必要，那么表達式需要保持簡單，同時通用轉換函數(shù)，以確保數(shù)據(jù)類型的一致性。