經驗誤差與過擬合
錯誤率為分類錯誤的樣本數占樣本總數的比例,相應的精度=1-錯誤率,模型的實際預測輸出與樣本的真實輸出之間的差異稱為“誤差”,模型在訓練集上的誤差稱為“訓練誤差”,在新樣本上的誤差稱為“泛化誤差”。我們希望得到在新樣本上表現好的學習器,也就是泛化誤差小的學習器,但是并不是泛化誤差越小越好,我們應該盡可能出訓練樣本中學出適用于所有潛在樣本的“普遍規律”,然而模型把訓練樣本學的太好,很可能把訓練完本自身的特點當做所有潛在樣本都具有的一般性質,這樣就導致了泛化性能下降,這種現象稱為“過擬合”,相對立的是“欠擬合”,是指訓練樣本的一般性質尚未學好。欠擬合比較容易克制,例如在決策樹學習中擴展分支、在神經網絡中增加訓練輪數,然而過擬合是無法避免的,我們所能做的就是盡量“緩解”,在現實生活中,我們往往有有多種學習算法可供選擇,對于同一算法,當使用不同參數配置時,也會產生不同的模型。
評估方法
通過“訓練集”訓練出機器學習模型,通過“測試集”來測試模型對新樣本的判別能力,然后以測試集上的“測試誤差”作為泛化誤差近似,當需要注意的是,測試集應該盡可能與測試集互斥,即測試樣本盡量不在訓練樣本中出現、未在訓練過程中使用。解釋為什么(老師出了10道習題供同學們練習,考試時老師又用同樣的這10道題作為考題,這個考試成績是否能反應出同學們真實情況,機器學習的模型是希望得到泛化能力強的模型,獲得舉一反三的能力)。
我們一共包含m個樣例的數據集D={(x1,y1),{x2,y2}...,(xm,ym)}},既要訓練,又要測試,我們通常對D進行適當的處理,從中產出訓練集S和測試集T。
留出法
“留出法”直接將數據集D劃分為兩個互斥的集合,其中一個集合作為訓練集S,另一個作為測試集T,D=S∪T,S∩T=? 需要注意的是,訓練/測試的劃分要盡可能的保持數據的一致性,避免應數據的劃分過程引入額外的偏差而對最終結果產生影響,也就是兩個集合中樣本類別比例要相似,這種保留類別比例的采樣方式稱為“分層采樣”。可即使是這樣,仍然存在多種劃分方式, 例如可以把D中的樣本排序,然后把前350個正例放到訓練集中,也可以把最后350個正例放到訓練集中,.....這不同的劃分將導致不同的訓練/測試集,模型估計必然會有偏差,
因此,單次使用留出法得到的估計結果往往不夠穩定可靠,在使用留出法時,一般要采用若干次隨機劃分、重復實驗取平均值作為留出法的結果。此外我們使用留出法對數據集D進行劃分,會有一個很尷尬的局面,當訓練集S過多,訓練出的模型可能更加接近用D訓練出的結局,但是由于測試集T太少,評估結果不夠穩定精確;若令訓練集T的樣本數過多,這訓練出的模型和用整個數據集D訓練出的模型相差就更加大了,這個問題沒有完美的解決方法,常見做法是將2/3~4/5的樣本用于訓練。
交叉驗證法
“交叉驗證法”先將數據集D劃分為k個大小相似的互斥子集,即 D = D1∪D2....∪Dk, Di∩ Dj= ?(i≠j),每個子集 Di都盡可能保持數據分布的一致性,即從D中通過分層采樣得到。然后,每次用k-1 個子集的并集作為訓練集,其余的那個子集作為測試集;這樣就可獲得k組訓練/測試集,從而可進行k 次訓練和測試,最終返回的是這k 個測試結果的均值。通常把交叉驗證法稱為“k折交叉驗證”。
與留出法類似,k折交叉驗證要隨機使用不同的劃分重復p次,最終的評估結果是這p 次k 折交叉驗證結果的均值。
“留一法”是數據集D包含m個樣本,若令 k=m,得到交叉驗證的一個特例,留一法不收隨機樣本劃分方式的影響,劃分方式為m個子集,每個子集一個樣本,使得訓練集和初始數據集只少一個樣本,所以被訓練出的模型很接近實際的評估模型,但是留一法也有缺點,當數據集m很大的時候,根本無法承受訓練m個模型的計算(m等于一百萬)。
自助法
給定包含m個樣本的數據集D,我們對它進行采樣產生數據集D': 每次隨機從D中挑選一個樣本7,將其拷貝放入D' 然后再將該樣本放回初始數據集D中,使得該樣本在下次采樣時仍有可能被采到,這個過程重復執行m 次后,我們就得到了包含m個樣本的數據集D',這就是自助采樣的結果,顯然,D 中有一部分樣本會在D'中多次出現,而另一部分樣本不出現.可以做一個簡單的估計,樣本在m 次采樣中始終不被采到的概率是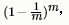 取極限得到
取極限得到
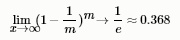
即通過自助來樣,初始數據集D 中約有36.8% 的樣本未出現在采樣數據集D'中.于是我們可將D' 用作訓練集, D\D' 用作測試集;這樣實際評估的模型與期望評估的模型都使用m個訓練樣本,而我們仍有數據總量約1/3 的、沒在訓練集中出現的樣本用于測試.這樣的測試結果,亦稱"包外估計"
自助法在數據集較小、難以有效劃分訓練/測試集是很有用;此外,自助法產生的數據集改變了初始數據集的分布,這會引起估計偏差,因此在數據量足夠大的時候還是留出法和交叉驗證法更常用一些。
調參與最終模型
在進行模型評估與選擇的時候,除了要對使用學習算法進行選擇,還需對算法參數進行設定,這就是常說的“參數調節”簡稱“調參”。對每種參數配置都訓練出模型,然后把最好的模型作為結果,但是對每種參數訓練出模型是不可行的,現實中常用的做法,是對每個參數選定一個范圍和變化步長,例如[0,0.2],步長選定0.05,則實際要評估的參數為5個,但即便是這樣同樣是不可行的,假設一個算法有3個參數,每個參數有5個候選參數,那么一共需要考慮53=125個模型,參數調的不好往往直接影響模型的關鍵性能。
這就需要在計算開銷和性能估計中進行折中考慮。
-
神經網絡
+關注
關注
42文章
4771瀏覽量
100718 -
機器學習
+關注
關注
66文章
8406瀏覽量
132567
發布評論請先 登錄
相關推薦
三種電路仿真軟件比較及器件模型加入方法
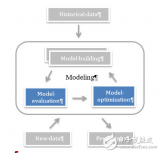
機器學習之模型評估和優化
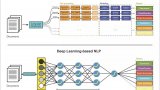
NLP的介紹和如何利用機器學習進行NLP以及三種NLP技術的詳細介紹
深度學習的三種學習模式介紹
靜電放電ESD三種模型及其防護設計





 機器學習模型的三種評估方法
機器學習模型的三種評估方法












評論