我們設計電路圖的時候,器件管腳之間的連線都是理想化的,但在實際的電路板上要通過有一定寬度、長度、厚度的導線進行連接,而且相鄰的導線之間還會由于電磁作用互相影響,實際的走線是有一定的阻抗、感抗、容抗的,導致了PCB上一系列干擾、串擾、信號完整性等問題。要保證PCB達到你設計所預期的性能,就要基于電磁場理論對“傳輸線”進行有效的設計。
相信大家時不時的都會聽到傳輸線(Transmission Line,TL)的概念,在信號完整性分析中占據重要地位。這一期我們就淺顯的學習下其基本概念和特性。 電路系統是器件(Device)和連線(Interconnect)的整體。在電路圖中經常使用的是理想連線。在集成電路中的制造中,連線的實現可能會用到多晶硅,鋁線或者銅線。封裝過程中的bonding wire可能會用到鋁線或者金線。板級pcb走線通常會用到銅線等等。
那么實際的互聯線的等效模型該怎么表示那?圖1給出了簡單的示意圖。理想走線當然不考慮其走線電阻、電容和電感等電氣特性,其特點就是等電勢(無延遲)。當然部分場合可根據需要簡單等效為集總(lumped)的L、R或C。或者使用復雜的RC模型、LC模型。最后可能是更完整的RLGC模型。
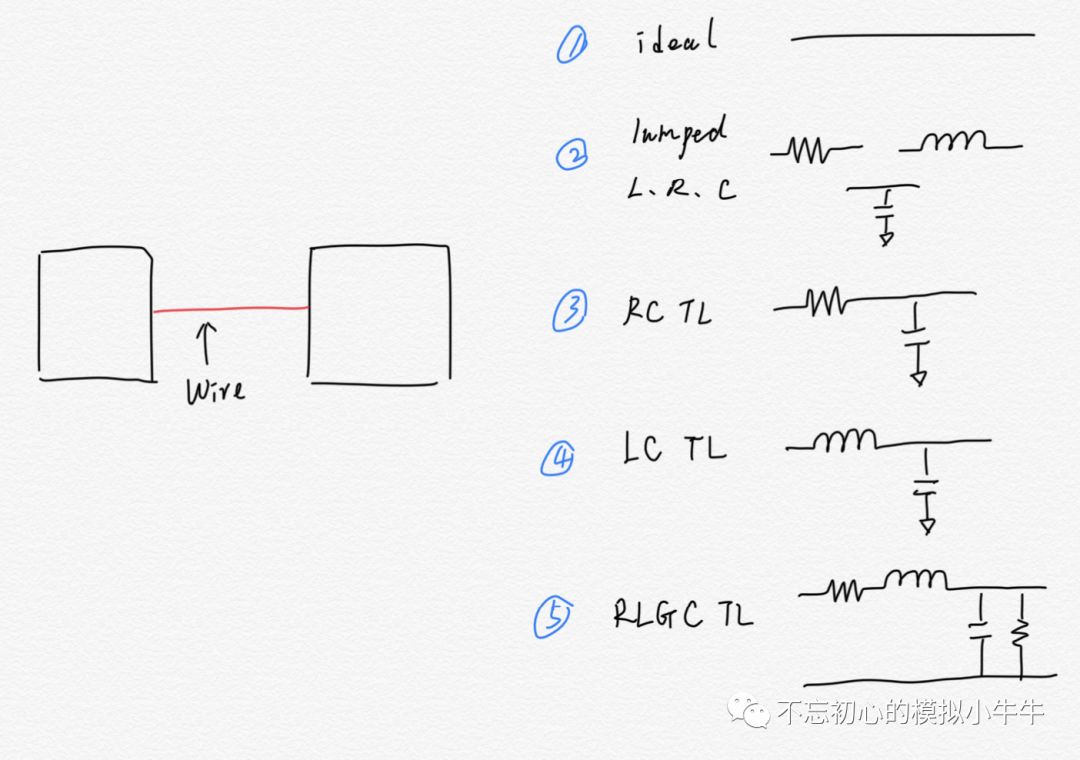
圖1 那么是不是什么時候都需要考慮RLGC模型那,當然不是了,這對于電路中成千上萬的連線也不現實。圖2給出了一些簡單的簡化等效場景。
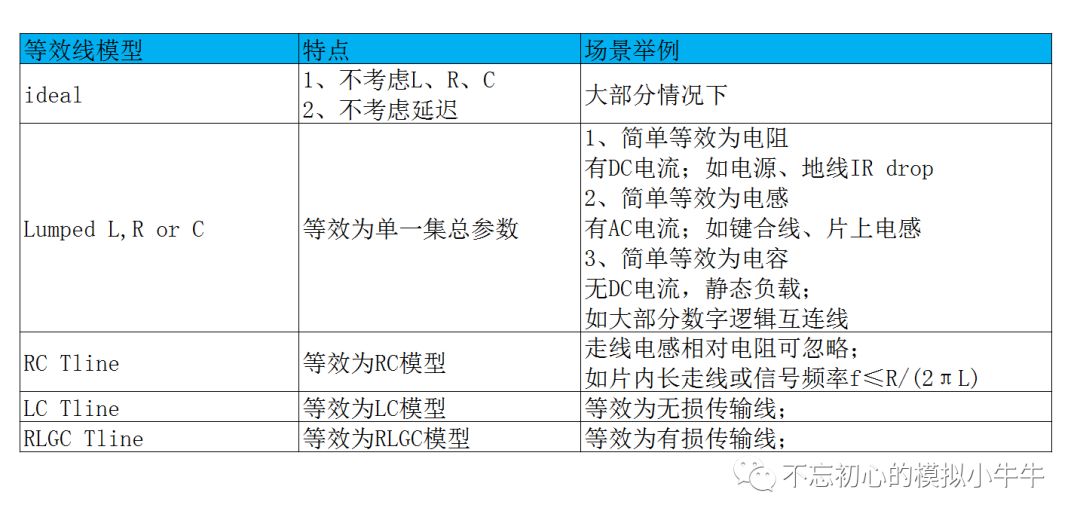
圖2 我們都知道信號在導線中的傳輸,本質上并不是電子的移動,而是電磁場以接近光速進行傳播。實際傳播速度由材質的相對介電常數εr和相對磁導率μr決定。那么如果知道了傳輸線的長度l,就可以得到傳輸線的延遲td=l/v。
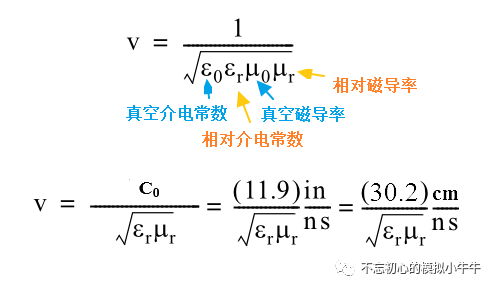
圖3 下面重點分析RLGC模型。既然以有限速度傳播,那么信號的傳播就有先后順序,圖4給出了無限長度傳輸線中某一點x和無限小增量dx的模型。其中R、L、G和C都是傳輸線單位長度的電阻、電感、電導和電容。電壓和電流都是位置x和時間t的函數,偏微分方程中當位置增量dx無限趨近于0時,能夠得到著名的傳輸線方程,也叫電報方程(telegraph equation )。
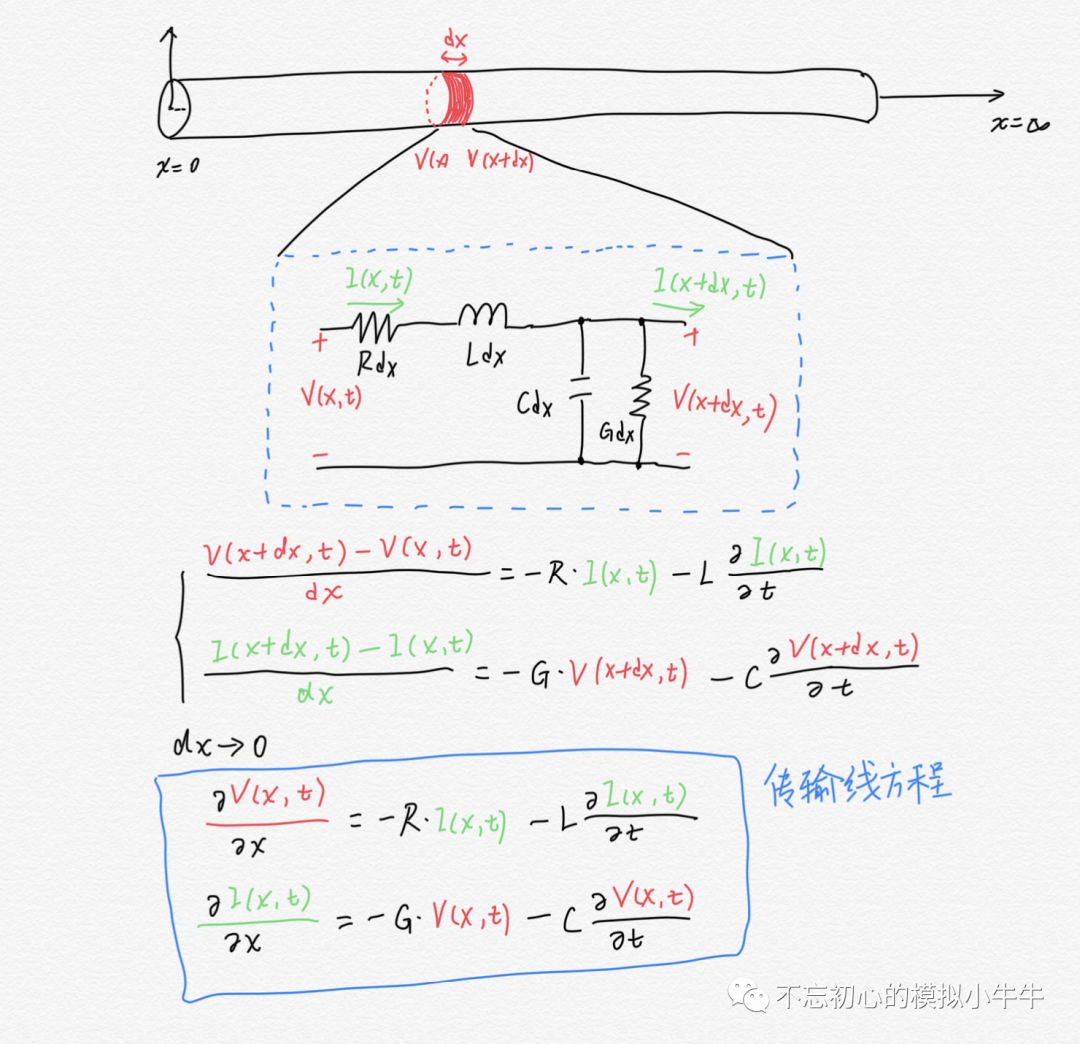
圖4 對傳輸線方程進行拉式變換并求解得到位置為x處的信號和x=0處信號的關系。如圖5中④式。其中γ稱之為傳播常數(propagation constant)。表明信號在傳輸線上傳輸時隨著傳輸距離x和頻率會發生變化。實部α影響單位距離幅度衰減,虛部β影響單位距離相位延遲。

圖5 對于傳輸線的阻抗計算,圖6給出思路,首先假設無限長度傳輸線的輸出阻抗為Z0如圖6(a),那么在(a)的基礎上,再增加無限小長度dx,取極限dx→0,阻抗仍然應該是Z0,如圖5(b)所示。最終我們得到的阻抗Z0的表達式。可以看到這是個和頻率及RLGC有關的量。當然如果不考慮R和G,也就是LC模型,也稱之為無損傳輸線(Lossless TL)模型。其阻抗就和頻率無關,也就是常說的無損傳輸線的特征阻抗(L/C)^0.5。
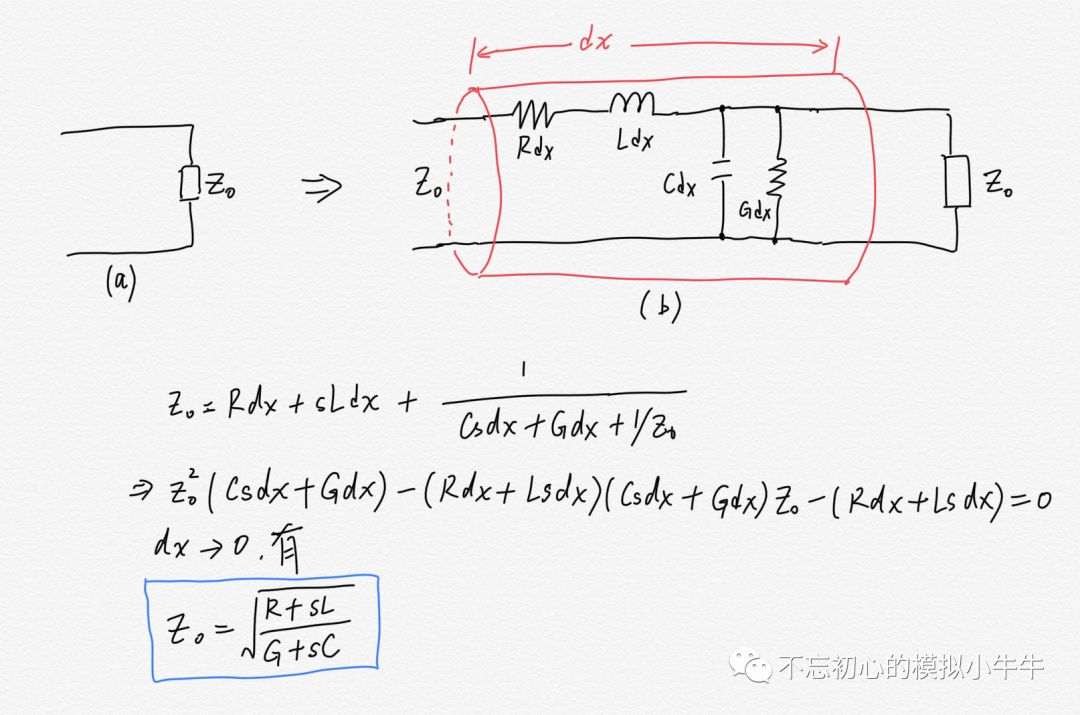
圖6 當然對于實際的的傳輸線為保證其阻抗恒定,避免出現阻抗不連續。需要傳輸線在其整個長度上具有均勻性(uniform)。圖7為一些常見pcb走線(trace)的剖面示意圖。包含了常見的雙絞線、同軸線,微帶線,帶狀線等剖面圖。在需要控制傳輸線的特征阻抗時,需要通過控制走線的寬度、厚度、間距等來設計L和C,從而達到可控阻抗(Controlled Impedance)的目的。比如常見的50歐姆。
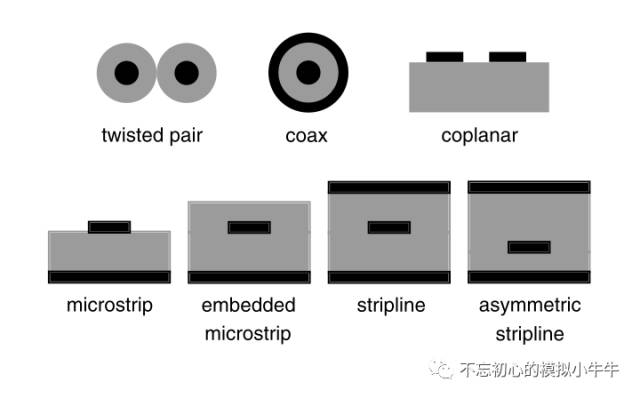
圖7 關于阻抗還可以形象地從信號的角度理解,信號在通過傳輸線的過程中需要對線上電容進行充電,對于一定的輸入信號幅度,瞬時電流的大小反映了瞬時阻抗( instantaneous impedance),如果傳輸線在其傳輸的路徑上是均勻的,信號能"看到"的阻抗就是固定的。如圖8所示。
圖8 之所以要討論傳輸線的特征阻抗,是因為在信號的傳輸過程遇到了阻抗不連續(不相等)就會出現信號的反射(Reflection)現象。也就是部分信號在不連續點繼續前進,部分折返朝源端傳播。對于這種情況有反射系數的定義。如圖9,當傳輸線出現阻抗為Z0和ZT的不連續處,需要通過反射電壓Vr的定義才能滿足邊界條。從而得到反射系數Kr的定義,即反射電壓Vr和入射電壓Vi的比例。
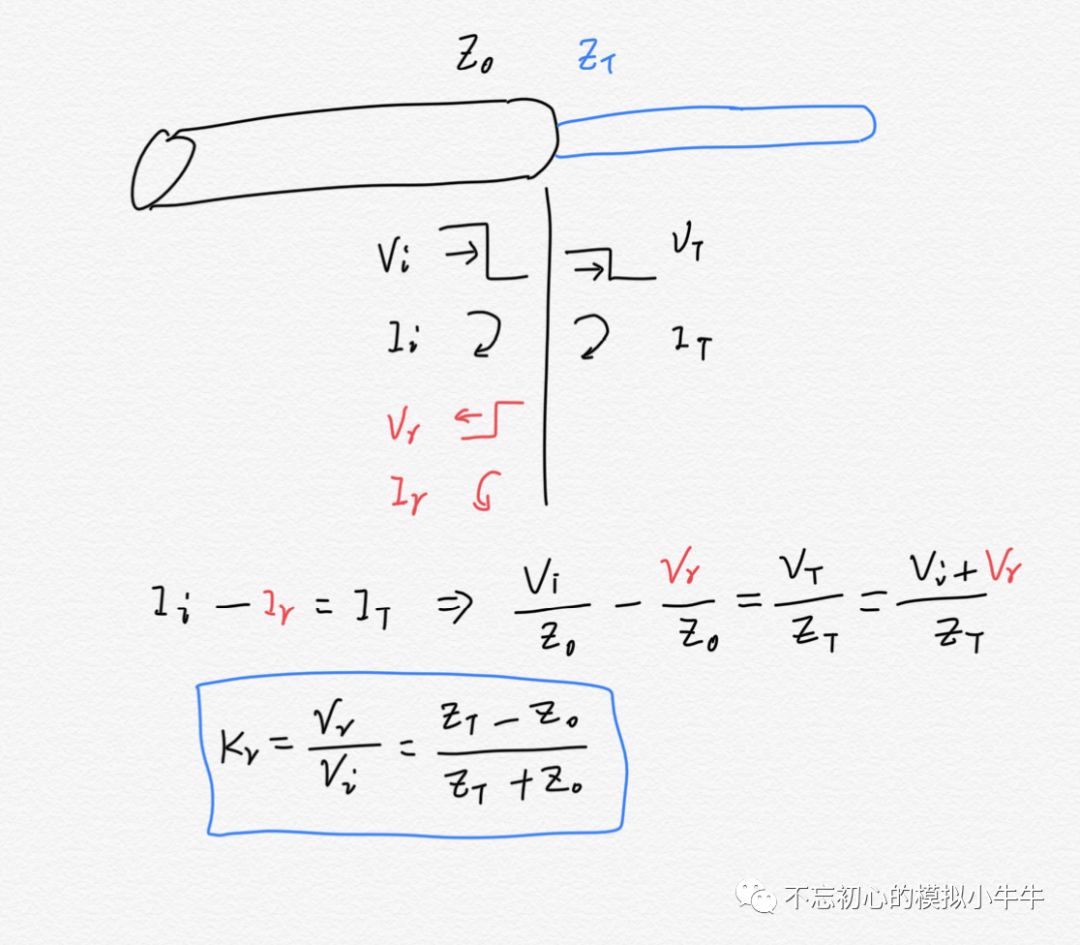
圖9 反射現象會影響到信號完整性,在實際的傳輸線應用中,當傳輸線設計是均勻一致時,為減小和避免反射問題,通常也需要傳輸線兩端的終端匹配的問題,通過端接電阻達到匹配目的,盡可能的使Kr接近0。降低由阻抗不連續引起的反射量。 所以,理想的連線和現實的導線是有差別的。平時遇到的各種坑,不是說理論就這樣,往往需要考慮也實際情況。
-
電路圖
+關注
關注
10349文章
10721瀏覽量
531354 -
電路板
+關注
關注
140文章
4967瀏覽量
98193 -
連線
+關注
關注
0文章
4瀏覽量
8165
發布評論請先 登錄
相關推薦
FPC電路板的優勢與劣勢
LDO穩壓器在電路板上的應用
電路板上vcc正極還是負極
電路板上的熱敏電阻有什么作用
使用探頭測量電路板上的電流的方法
電位器上的電路板的作用
電路板維修用什么儀器檢查
如何檢測電路板上的元件
電路板檢修用什么檔位好
電路板測試是什么工作 電路板測試對身體有害嗎
電路板測試工裝制作原理是什么
電路板測試步驟有哪些 電路板測試儀器有哪些
如何正確檢測電路板上的元件是否正常
閱讀電路板電路原理圖的方法




 電路板上的連線也存在的坑
電路板上的連線也存在的坑










評論