根據(jù)受歡迎程度，線性回歸和邏輯回歸經(jīng)常是我們做預(yù)測模型時(shí)，且第一個學(xué)習(xí)的算法。但是如果認(rèn)為回歸就兩個算法，就大錯特錯了。事實(shí)上我們有許多類型的回歸方法可以去建模。每一個算法都有其重要性和特殊性。

內(nèi)容

1.什么是回歸分析？

2.我們?yōu)槭裁匆褂没貧w分析？

3.回歸有哪些類型 ？

4.線性回歸

5.邏輯回歸

6.多項(xiàng)式回歸

7.逐步回歸

8.嶺回歸

9.Lasso回歸

10.ElasticNet回歸

什么是回歸分析？

回歸分析是研究自變量和因變量之間關(guān)系的一種預(yù)測模型技術(shù)。這些技術(shù)應(yīng)用于預(yù)測，時(shí)間序列模型和找到變量之間關(guān)系。例如可以通過回歸去研究超速與交通事故發(fā)生次數(shù)的關(guān)系。

我們?yōu)槭裁匆没貧w分析？

這里有一些使用回歸分析的好處：它指示出自變量與因變量之間的顯著關(guān)系；它指示出多個自變量對因變量的影響。回歸分析允許我們比較不同尺度的變量，例如：價(jià)格改變的影響和宣傳活動的次數(shù)。這些好處可以幫助市場研究者／數(shù)據(jù)分析師去除和評價(jià)用于建立預(yù)測模型里面的變量。

回歸有哪些類型？

我們有很多種回歸方法用預(yù)測。這些技術(shù)可通過三種方法分類：自變量的個數(shù)、因變量的類型和回歸線的形狀。

1.線性回歸

線性回歸可謂是世界上最知名的建模方法之一，也是應(yīng)該是我們第一個接觸的模型。在模型中，因變量是連續(xù)型的，自變量可以使連續(xù)型或離散型的，回歸線是線性的。

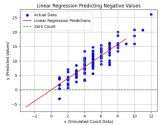
線性回歸用最適直線（回歸線）去建立因變量Y和一個或多個自變量X之間的關(guān)系。可以用公式來表示：

Y=a+b*X+e

a為截距，b為回歸線的斜率，e是誤差項(xiàng)。

簡單線性回歸與多元線性回歸的差別在于：多元線性回歸有多個（》1）自變量，而簡單線性回歸只有一個自變量。到現(xiàn)在我們的問題就是：如何找到那條回歸線？

我們可以通過最小二乘法把這個問題解決。其實(shí)最小二乘法就是線性回歸模型的損失函數(shù)，只要把損失函數(shù)做到最小時(shí)得出的參數(shù)，才是我們最需要的參數(shù)。

我們一般用決定系數(shù)（R方）去評價(jià)模型的表現(xiàn)。

重點(diǎn)：

1.自變量與因變量之間必須要有線性關(guān)系。

2.多重共線性、自相關(guān)和異方差對多元線性回歸的影響很大。

3.線性回歸對異常值非常敏感，其能嚴(yán)重影響回歸線，最終影響預(yù)測值。

4.在多元的自變量中，我們可以通過前進(jìn)法，后退法和逐步法去選擇最顯著的自變量。

2. 邏輯回歸

邏輯回歸是用來找到事件成功或事件失敗的概率。當(dāng)我們的因變量是二分類（0/1，True/False，Yes/No）時(shí)我們應(yīng)該使用邏輯回歸。

重點(diǎn)：

1.在分類問題中使用的非常多。

2.邏輯回歸因其應(yīng)用非線性log轉(zhuǎn)換方法，使得其不需要自變量與因變量之間有線性關(guān)系。

3.為防止過擬合和低擬合，我們應(yīng)該確保每個變量是顯著的。應(yīng)該使用逐步回歸方法去估計(jì)邏輯回歸。

4.邏輯回歸需要大樣本量，因?yàn)樽畲笏迫还烙?jì)在低樣本量的情況下表現(xiàn)不好。

5.要求沒有共線性。

6.如果因變量是序數(shù)型的，則稱為序數(shù)型邏輯回歸。

7.如果因變量有多個，則稱為多項(xiàng)邏輯回歸。

3. 多項(xiàng)式回歸

如果一個回歸，它的自變量指數(shù)超過1，則稱為多項(xiàng)式回歸。可以用公式表示：

y = a + b * x^2

在這個回歸技術(shù)中，最適的線不是一條直線，而是一條曲線。

重點(diǎn)：

① 很多情況下，我們?yōu)榱私档驼`差，經(jīng)常會抵制不了使用多項(xiàng)式回歸的誘惑，但事實(shí)是，我們經(jīng)常會造成過擬合。所以要經(jīng)常的把數(shù)據(jù)可視化，觀察數(shù)據(jù)與模型的擬合程度。

② 特別是要看曲線的結(jié)尾部分，看它的形狀和趨勢是否有意義。高的多項(xiàng)式往往會產(chǎn)生特別古怪的預(yù)測值。

4. 逐步回歸

當(dāng)我們要處理多個自變量時(shí)，我們就需要這個回歸方法。在這個方法中選擇變量都是通過自動過程實(shí)現(xiàn)的，不需要人的干預(yù)。

這個工程是通過觀察統(tǒng)計(jì)值，比如判定系數(shù)，t值和最小信息準(zhǔn)則等去篩選變量。逐步回歸變量一般是基于特定的標(biāo)準(zhǔn)加入或移除變量來擬合回歸模型。

一些常用的逐步回歸方法如下：

1. 標(biāo)準(zhǔn)逐步回歸做兩件事情。只要是需要每一步它都會添加或移除一些變量。

2. 前進(jìn)法是開始于最顯著的變量然后在模型中逐漸增加次顯著變量。

3. 后退法是開始于所有變量，然后逐漸移除一些不顯著變量。

4. 這個模型技術(shù)的目的是為了用最少的變量去最大化模型的預(yù)測能力。它也是一種降維技術(shù)。

5. 嶺回歸

當(dāng)碰到數(shù)據(jù)有多重共線性時(shí)，我們就會用到嶺回歸。所謂多重共線性，簡單的說就是自變量之間有高度相關(guān)關(guān)系。在多重共線性中，即使是最小二乘法是無偏的，它們的方差也會很大。通過在回歸中加入一些偏差，嶺回歸酒會減少標(biāo)準(zhǔn)誤差。

‘嶺回歸是一種專用于共線性數(shù)據(jù)分析的有偏估計(jì)回歸方法，實(shí)質(zhì)上是一種改良的最小二乘估計(jì)法，通過放棄最小二乘法的無偏性，以損失部分信息、降低精度為代價(jià)獲得回歸系數(shù)更為符合實(shí)際、更可靠的回歸方法，對病態(tài)數(shù)據(jù)的擬合要強(qiáng)于最小二乘法。’ －－－百度百科

嶺回歸是通過嶺參數(shù)λ去解決多重共線性的問題。看下面的公式：

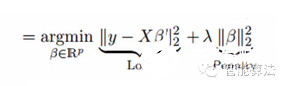
其中l(wèi)oss為損失函數(shù)，penalty為懲罰項(xiàng)。

重點(diǎn)：

1.嶺回歸的假設(shè)與最小二乘法回歸的假設(shè)相同除了假設(shè)正態(tài)性。

2.它把系數(shù)的值收縮了，但是不會為0.

3.正則化方法是使用了l2正則。

6. LASSO回歸

和嶺回歸類似，Lasso（least Absolute Shrinkage and Selection Operator）也是通過懲罰其回歸系數(shù)的絕對值。看下面的公式：

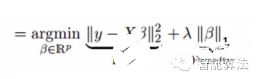
Lasso回歸和嶺回歸不同的是，Lasso回歸在懲罰方程中用的是絕對值，而不是平方。這就使得懲罰后的值可能會變成0.

重點(diǎn)：

1.其假設(shè)與最小二乘回歸相同除了正態(tài)性。

2.其能把系數(shù)收縮到0，使得其能幫助特征選擇。

3.這個正則化方法為l1正則化。

4.如果一組變量是高度相關(guān)的，lasso會選擇其中的一個，然后把其他都變?yōu)?.

7. ElasticNet回歸

ElasticNet回歸是Lasso回歸和嶺回歸的組合。它會事先訓(xùn)練L1和L2作為懲罰項(xiàng)。當(dāng)許多變量是相關(guān)的時(shí)候，Elastic-net是有用的。Lasso一般會隨機(jī)選擇其中一個，而Elastic-net則會選在兩個。

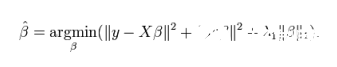
與Lasso和嶺回歸的利弊比較，一個實(shí)用的優(yōu)點(diǎn)就是Elastic-Net會繼承一些嶺回歸的穩(wěn)定性。

重點(diǎn)：

1.在選擇變量的數(shù)量上沒有限制

2.雙重收縮對其有影響

3.除了這7個常用的回歸技術(shù)，你也可以看看貝葉斯回歸、生態(tài)學(xué)回歸和魯棒回歸。

如何選擇回歸模型？

面對如此多的回歸模型，最重要的是根據(jù)自變量因變量的類型、數(shù)據(jù)的維數(shù)和其他數(shù)據(jù)的重要特征去選擇最合適的方法。以下是我們選擇正確回歸模型時(shí)要主要考慮的因素：

1.數(shù)據(jù)探索是建立預(yù)測模型不可或缺的部分。它應(yīng)該是在選擇正確模型之前要做的。

2.為了比較不同模型的擬合程度，我們可以分析不同的度量，比如統(tǒng)計(jì)顯著性參數(shù)、R方、調(diào)整R方、最小信息標(biāo)準(zhǔn)、BIC和誤差準(zhǔn)則。另一個是Mallow‘s Cp準(zhǔn)則。

3.交叉驗(yàn)證是驗(yàn)證預(yù)測模型最好的方法。你把你的數(shù)據(jù)集分成兩組：一組用于訓(xùn)練，一組用于驗(yàn)證。

4.如果你的數(shù)據(jù)集有許多讓你困惑的變量，你就不應(yīng)該用自動模型選擇方法，因?yàn)槟悴幌氚堰@些變量放在模型當(dāng)中。

5.不強(qiáng)大的模型往往容易建立，而強(qiáng)大的模型很難建立。

6.回歸正則方法在高維度和多重共線性的情況下表現(xiàn)的很好。