我們知道,磁感應(yīng)強(qiáng)度是一種矢量,所以在存在多個(gè)磁場(chǎng)的空間區(qū)域內(nèi),復(fù)合磁場(chǎng)的計(jì)算需要用到矢量運(yùn)算的知識(shí)。
我們以一道奧賽真題為例來說明矢量運(yùn)算在磁場(chǎng)中的應(yīng)用。
例空間某區(qū)域內(nèi)存在兩個(gè)勻強(qiáng)磁場(chǎng),其中一個(gè)勻強(qiáng)磁場(chǎng)B1的方向平行紙面向右,磁感應(yīng)強(qiáng)度B1=1T,長L=1m的直導(dǎo)線通有I=1A的恒定電流,當(dāng)導(dǎo)線平行于紙面與B1成60度夾角時(shí),其所受到的安培力為0,而將導(dǎo)線垂直于紙面放置時(shí),測(cè)得其所受到的安培力大小為2N,求另一勻強(qiáng)磁場(chǎng)B2的磁感應(yīng)強(qiáng)度大小。
分析:一般情況下,通電導(dǎo)線在磁場(chǎng)中將受到安培力的作用,那什么時(shí)候受力為0呢?只有在導(dǎo)線與磁感應(yīng)強(qiáng)度的方向平行的時(shí)候才不受力。所以B1與B2的合磁感應(yīng)強(qiáng)度B與導(dǎo)線的夾角應(yīng)該0度或者180度,并且平行于紙面,畫出磁感應(yīng)強(qiáng)度的矢量圖如下。
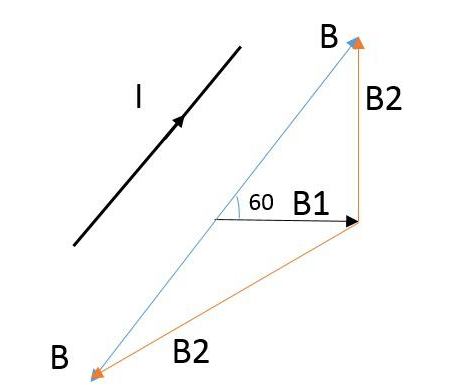
而當(dāng)導(dǎo)線垂直于紙面時(shí)顯然導(dǎo)線也垂直于合磁感應(yīng)強(qiáng)度B,此時(shí)導(dǎo)線所受的安培力
F=BIL=2N,解得B=2T
已知B和B1的兩個(gè)矢量的大小和方向,運(yùn)用矢量加減法的規(guī)則和余弦定理即可求出B2的大小為
B2=√3T或者√7T,方向如圖中紅線標(biāo)示。
考察點(diǎn):
1、安培力方向、磁場(chǎng)方向和電流方向三者之間的關(guān)系(左手定則);
2、矢量合成(矢量相加與矢量相減);
3、三角公式余弦定理的運(yùn)用。
-
磁場(chǎng)
+關(guān)注
關(guān)注
3文章
901瀏覽量
24857 -
矢量運(yùn)算
+關(guān)注
關(guān)注
0文章
3瀏覽量
1481
發(fā)布評(píng)論請(qǐng)先 登錄
矩陣變換器-異步電機(jī)矢量控制系統(tǒng)仿真研究
電機(jī)控制中矢量圖的作用(可下載)
磁場(chǎng)是怎么回事?磁場(chǎng)是怎么形成的?

如何利用磁場(chǎng)相機(jī)實(shí)現(xiàn)先進(jìn)的磁性微結(jié)構(gòu)分析?




















評(píng)論