浮點(diǎn)數(shù),是屬于有理數(shù)中某特定子集的數(shù)的數(shù)字表示,在計(jì)算機(jī)中用以近似表示任意某個(gè)實(shí)數(shù)。具體的說,這個(gè)實(shí)數(shù)由一個(gè)整數(shù)或定點(diǎn)數(shù)(即尾數(shù))乘以某個(gè)基數(shù)(計(jì)算機(jī)中通常是2)的整數(shù)次冪得到,這種表示方法類似于基數(shù)為10的科學(xué)計(jì)數(shù)法。
1 、浮點(diǎn)數(shù)基礎(chǔ)知識(shí)
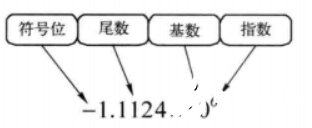
浮點(diǎn)數(shù)由四部分構(gòu)成:符號(hào)位(Sign Bit)、尾數(shù)(Mantissa)、基數(shù)(Radix)和指數(shù)(Exponent)。根據(jù)《IEEE Standard 754 for Binary Floating-Point Arithmetic》的定義–二進(jìn)制標(biāo)準(zhǔn)浮點(diǎn)數(shù),基數(shù)為2。s、m、e分別為符號(hào)數(shù)、尾數(shù)和指數(shù),n為相應(yīng)的浮點(diǎn)數(shù)值。

IEEE-754規(guī)定了三種浮點(diǎn)數(shù):?jiǎn)尉龋╢loat)、雙精度(double)和擴(kuò)展精度。
其中單精度為32bit,其中包含1位符號(hào)位S,8位指數(shù)位E和23位尾數(shù)位M。S、E、M為相應(yīng)的二進(jìn)制序列。
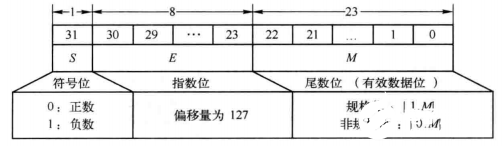
S:
正數(shù) 0.1xxxxxx
負(fù)數(shù) 1.1xxxxxx
M:
表示小數(shù)點(diǎn)之后的二進(jìn)制尾數(shù)。
M為0110表示:二進(jìn)制.0110
E:
規(guī)格化(normalized)
非規(guī)格化(denormalized)
2 、規(guī)格化浮點(diǎn)數(shù)
E表示的二進(jìn)制不全為0也不全為1時(shí)該浮點(diǎn)數(shù)為規(guī)格化浮點(diǎn)數(shù)。

e表示偏置(Biased)
|E|表示E的二進(jìn)制整數(shù)
bias表示偏置
k為指數(shù)位寬
對(duì)于單精度浮點(diǎn)數(shù)來說k為8,所以bias為127。E=“10001000”為例,|E|=136,故e為9。
對(duì)于規(guī)格化浮點(diǎn)數(shù),標(biāo)準(zhǔn)規(guī)定尾數(shù)位小數(shù)點(diǎn)左側(cè)的隱含位為1,所以:
m = |1.M|
例如M=“10010…0”則1.M=“1.10010…0”所以m=1.5625

s=0
m = 1.5625
e =9
n =55.5112
單精度浮點(diǎn)數(shù)的公式可表示為:
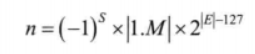
3、非規(guī)格化浮點(diǎn)數(shù)
E的二進(jìn)制位全為0時(shí)該浮點(diǎn)數(shù)為非規(guī)格化浮點(diǎn)數(shù)。
bias=127
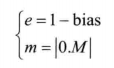
單精度非規(guī)格化浮點(diǎn)數(shù)公式:
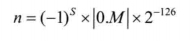
-0.0 符號(hào)位為1,其余位為0.
+0.0全部為0.
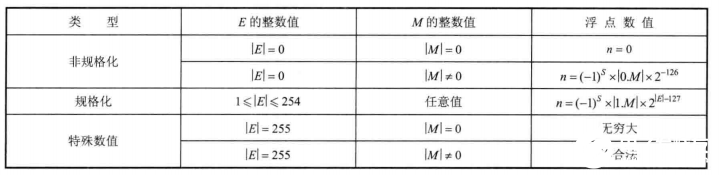
4、特殊數(shù)值
E的二進(jìn)制位全為1時(shí)為特殊數(shù)值。
M全0,n無窮大
M全1,S為1,n負(fù)無窮大
M全1,S為0,n正無窮大
M不全為0和1,n NaN(Not a Number)
5 、雙精度浮點(diǎn)數(shù)
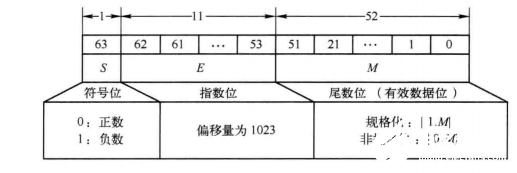
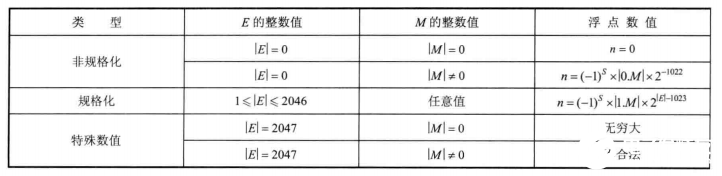
IEEE-754定義雙精度浮點(diǎn)數(shù)共64bit 。1位符號(hào)位S,11位指數(shù)位E和52位尾數(shù)位M。同樣可以劃分為規(guī)格化、非規(guī)格化和特殊數(shù)值。
-
計(jì)算機(jī)
+關(guān)注
關(guān)注
19文章
7688瀏覽量
91156 -
浮點(diǎn)數(shù)
+關(guān)注
關(guān)注
0文章
61瀏覽量
16158
發(fā)布評(píng)論請(qǐng)先 登錄
FPGA定點(diǎn)和浮點(diǎn)數(shù)學(xué)運(yùn)算實(shí)例對(duì)比
想在bsp工程打印浮點(diǎn)數(shù),結(jié)果找不到rt_vsnprintf_full軟件包,怎么解決?
PRINTF函數(shù)無法打印出浮點(diǎn)數(shù)內(nèi)容是為什么?
設(shè)計(jì)了一個(gè)基于浮點(diǎn)數(shù)運(yùn)算的協(xié)處理器,使用C語言編程時(shí)沒法輸入float型數(shù)據(jù),請(qǐng)問有哪些部分需要修改?
labview數(shù)據(jù)類型與PLC 數(shù)據(jù)類型之間的轉(zhuǎn)換(來自于寫入浮點(diǎn)數(shù)到匯川 PLC中的數(shù)據(jù)轉(zhuǎn)換關(guān)鍵的修改)
西門子TIA Portal如何比較兩個(gè)浮點(diǎn)數(shù)相等
ADS1282采集到的數(shù)據(jù)傳到PC上應(yīng)該怎么轉(zhuǎn)為浮點(diǎn)數(shù)?
基于FPGA的數(shù)字信號(hào)處理——浮點(diǎn)數(shù)

TLV320AIC3106音頻芯片怎么發(fā)送、接收浮點(diǎn)數(shù)呢?
labview中浮點(diǎn)數(shù)與十六進(jìn)制字符串相互轉(zhuǎn)化
TMS320C6745浮點(diǎn)數(shù)字信號(hào)處理器技術(shù)簡(jiǎn)介

C9230C100 TMS320C672x浮點(diǎn)數(shù)字信號(hào)處理器ROM




















評(píng)論