圖像卷積概念
圖像卷積操作(convolution),或稱為核操作(kernel),是進行圖像處理的一種常用手段,
圖像卷積操作的目的是利用像素點和其鄰域像素之前的空間關系,通過加權求和的操作,實現模糊(blurring),銳化(sharpening),邊緣檢測(edge detection)等功能。
圖像卷積的計算過程就是卷積核按步長對圖像局部像素塊進行加權求和的過程。
卷積核實質上是一個固定大小的權重數組,該數組中的錨點通常位于中心。
卷積核大小
通常情況下,選取卷積核大小為1x1,3x3,5x5,7x7等
取奇數大小的目的是為了設置卷積核中心為錨點,方便卷積核和圖像的對齊處理
設置卷積核大小對稱的目的是為了在空間域中充分利用像素點和其領域像素間的關系。當然這不是必須的,如果需要針對某一軸進行處理,可以設置1x3或3x1大小。
參考:
Convolution
Kernel (image processing)
圖像卷積數學公式
二維離散卷積公式如下:
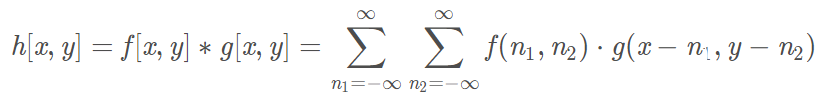
圖像卷積通常使用這個公式,其中g[x,y]g[x,y]g[x,y]為卷積核,符號?ast?表示卷積操作
圖形化表示
以一維離散卷積公式為例:
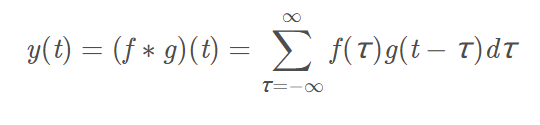
其圖形化公式如下:
首先將函數 g(τ) 反射為 g(?τ) ,相當于 g(τ) 沿yyy軸翻轉
再對函數 g(?τ) 添加一個時間偏移量 t ,它允許函數 g(t?τ) 沿著 τ 軸移動
變量 t 每增加 1,表示函數 g(t?τ) 向左移動一步
計算 t 遍歷 ?∞ 到 ∞ 的過程中,函數 f(τ) 和 g(t?τ) 的重疊面積
舉例
函數 f = [1,2,3,4] ,函數 g = [1,3,2]
將函數 g 逆轉:g(τ) ? g(?τ),值變為[2,3,1]
計算過程如下:
h(0)=[1]?[1]=1?1=1
h(1)=[1,2]?[3,1]=1?3+2?1=3+2=5
h(2)=[1,2,3]?[2,3,1]=1?2+2?3+3?1=2+6+3=11
h(3)=[2,3,4]?[2,3,1]=2?2+3?3+4?1=4+9+4=17
h(4)=[3,4]?[2,3]=3?2+4?3=6+12=18
h(5)=[4]?[2]=4?2=8
h(x)=[1,5,11,17,18,8]
以此類推可知二維離散卷積的計算過程,先對角翻轉卷積核,在逐步向兩個正方向移動,計算重疊面積
flip the mask (horizontally and vertically) only once(水平和垂直翻轉掩模一次)
slide the mask onto the image(在圖像上滑動掩模)
multiply the corresponding elements and then add them(將相應的元素相乘,然后求和)
repeat this procedure until all values of the image has been calculated(重復這一過程,直到所有圖像值均已被計算)
多說一句,關于信號與系統中的LTI(linear time-invariant systems,線性時不變系統)和LSI(linear shift invariant system,線性位移不變系統)的不變性一直沒太理解,圖形化理解就是信號(函數)可以隨著時間/空間移動而不改變它的原先的形狀,就像卷積核一樣。
圖像卷積注意事項
在進行卷積操作時,需要注意兩點
卷積核歸一化
卷積核的大小和值可以根據要求定義,但通常會將整個卷積核進行歸一化操作,其目的是為了保證修改后結果圖像的平均元素值和原始圖像平均元素值一樣。
因為卷積操作滿足齊次性,所以可以卷積計算完成后再除以整個卷積核的值。
數值精度
圖像數值類型通常為uint8,在進行卷積操作時很容易造成數值溢出,所以在進行操作之前可以先轉換成更高精度的數值類型
-
卷積
+關注
關注
0文章
95瀏覽量
18775
發布評論請先 登錄
依托raksmart服務器在多種系統上本地部署deepseek注意事項
EE-276:Blackfin處理器上圖像處理的視頻框架注意事項























評論