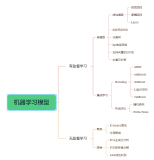
1、類型

主要有兩種類型：數據集變換和聚類。

無監督變換：

降維：接受數據的高維表示，找到新的表示方法，以用較少的特征概括重要特性。

找到“構成”數據的各個組成部分。例如，文本的主題提取。

聚類：

將數據劃分成不同的組，每組包含相似的物項

2、降維

1. 主成分分析（PCA）

一種旋轉數據集的方法，旋轉后的特征在統計上不相關。旋轉后，通常根據新特征對數據集的重要性來選擇它的一個子集。

主成分

方差最大的方向為“成分1”，這是包含包含最多信息的方向。之后找到與“成分1”正交的包含信息最多的方向，得到“成分2”……利用這一過程找到的方向成為主成分。通常，主成分的個數與原始特征相同。

在PCA找到的額旋轉表示中，坐標軸之間 不相關。

應用

高維數據集可視化

特征提取：找到一種數據表示，比給定的原始表示更適合于分析。

對PCA模型的另一種理解：僅適用一些成分對原始數據進行重建。

2. 非負矩陣分解（NMF）

在NMF中，目標是分量和系數均為非負。只能應用于每個特征都是非負的數據，因為非負分量的非負求和不可能得到負值。

與PCA不同，減少分量個數不僅會刪除一些方向，而且會創建一組完全不同的分量。

NMF的分量沒有按任何特定方法排序，所有分量的地位平等。

NMF使用了隨機初始化，根據隨機種子的不同可能會產生不同的結果。

3. t-SNE與流形學習

流形學習算法 ：主要用于可視化，允許進行更復雜的映射。只能變換用于訓練的數據。

t-SNE：找到數據的一個二維表示，盡可能保持數據點之間的距離。試圖保存那些點比較靠近的信息。

3、聚類

聚類：將數據集劃分成組的任務，這些組叫做簇。

1. K均值聚類

原理

試圖找到代表數據特定區域的簇中心。

算法過程

① 將每個數據點分配給最近的簇中心

② 將每個簇中心設置為所分配的所有數據點的平均值，如果簇的分配不再變化，結束；反之，執行步驟1

注：聚類算法與分類算法類似，但不存在真實的標簽，標簽本身沒有先驗意義。

注意

每個簇僅由其中心決定，這意味著每個簇都是凸型的，因此，只能找到相對簡單的形狀。

k均值假設所有簇在某種程度上有相同的直徑，它總是將簇之間的邊界剛好畫在簇中心的中間位置

k均值假設所有方向對每個簇同等重要

特點

優點：

容易理解和實現

運行速度相對較快

擴展到大型數據集比較容易

缺點：

依賴于隨機初始化

對簇形狀的假設的約束性較強

要求制定所要尋找到簇的個數

2. 凝聚聚類

算法首先聲明每個點是自己的簇，然后合并兩個最相似的簇，直到滿足某種停止準則為止。

連接準則：規定如何度量“最相似的簇”。

① ward型：兩個簇合并后，使得所有簇中方差增加最小

② average型：平均距離最小的兩個簇合并

③ complete型：簇中點之間最大距離最小的兩個簇合并

注：凝聚算法不能對新數據點做出預測

凝聚聚類生成了所謂的層次聚類

3. DBSCAN （具有噪聲的基于密度的空間聚類應用）

原理

識別特征空間的“擁擠”區域中的點，這些區域成為密集區域。簇形成數據的密集區域，并由相對較空的區域分隔開。在密集區域中的點成為核心樣本，指定參數eps和min_samples。如果在一個點eps的距離內至少有min_samples個數據點，則為核心樣本。

算法過程

① 任意選取一個點，檢查是否是核心樣本。

② 若不是，標記為噪聲。反之，標記為核心樣本，并分配一個新的簇標簽。然后檢查鄰居，若未被分配，分配簇標簽；如果是核心樣本，依次訪問鄰居。

③ 選取另一個尚未被訪問過的點，重復以上過程。

最后得到三種點：核心點、邊界點、噪聲。

特點

優點：

不需先驗設置簇的個數

可以劃分具有復雜形狀的簇

可以找出不屬于任何簇的點

缺點：

不允許對新的測試數據進行預測

聚類評估

1. 真實值評估

調整rand指數（ARI），歸一化互信息（NMI）

二者都給出了定量的度量，最佳值為1，0表示不相關的聚類。

2. 沒有真實值

輪廓系數 計算一個簇的緊致度，值越大越好，最高分數為1。雖然緊致的簇很好，但不允許復雜的形狀。

聚類小結

k均值

可以用簇的平均值來表示簇。

可被看做是一種分解方法，。每個數據點都由其簇中心表示

DBSCAN

可以檢測噪聲點

可以自動判斷簇的數量

允許簇有復雜的形狀

有時會生成大小差別很大的簇，可能是優點可能是缺點

凝聚聚類

可以提供數據的可能劃分的整個層次結構

可以通過樹狀圖查看