近來，圖神經網絡（GNN）在各個領域廣受關注，比如社交網絡，知識圖譜，推薦系統以及生命科學。GNN在對圖節點之間依賴關系進行建模的強大功能使得與圖分析相關的研究領域取得了突破。 本文旨在介紹圖形神經網絡的基礎知識兩種較高級的算法，DeepWalk和GraphSage。

圖

在我們學習GAN之前，大家先了解一下什么圖。在計算機科學中，圖是一種數據結構，由頂點和邊組成。圖G可以通過頂點集合V和它包含的邊E來進行描述。

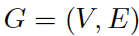
根據頂點之間是否存在方向性，邊可以是有向或無向的。

頂點通常稱為節點。在本文中，這兩個術語是可以互換的。

圖神經網絡

圖神經網絡是一種直接在圖結構上運行的神經網絡。GNN的一個典型應用是節點分類。本質上，圖中的每個節點都與一個標簽相關聯，我們希望預測未標記節點的標簽。本節將介紹論文中描述的算法，GNN的第一個提法，因此通常被視為原始GNN。

在節點分類問題中，每個節點v都可以用其特征x_v表示并且與已標記的標簽t_v相關聯。給定部分標記的圖G，目標是利用這些標記的節點來預測未標記的節點標簽。 它通過學習得到每個節點的d維向量（狀態）表示h_v，同時包含其鄰居的信息。

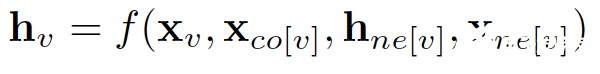
https://arxiv.org/pdf/1812.08434

x_co［v］ 代表連接頂點v的邊的特征，h_ne［v］代表頂點v的鄰居節點的嵌入表示，x_ne［v］代表頂點v的鄰居節點特征。f是將輸入投影到d維空間的轉移函數。由于要求出h_v的唯一解，我們應用Banach不動點理論重寫上述方程進行迭代更新。

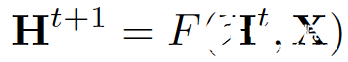
https://arxiv.org/pdf/1812.08434

H和X分別表示所有h和x的連接。

通過將狀態h_v以及特征x_v傳遞給輸出函數g來計算GNN的輸出。

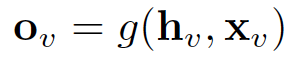
https://arxiv.org/pdf/1812.08434

這里的f和g都可以解釋為全連接前饋神經網絡。 L1損失可以直接表述如下：

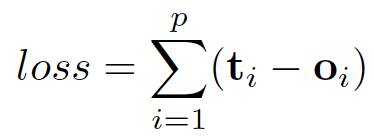
https://arxiv.org/pdf/1812.08434

可以通過梯度下降優化。

但是，本文指出的原始GNN有三個主要局限：

如果放寬了“固定點”的假設，則可以利用多層感知器來學習更穩定的表示，并刪除迭代更新過程。 這是因為，在原始方法中，不同的迭代使用轉移函數f的相同參數，而不同MLP層中的不同參數允許分層特征提取。

它不能處理邊緣信息（例如知識圖譜中的不同邊可能表示節點之間的不同關系）

固定點會限制節點分布的多樣化，因此可能不適合學習節點表示。

已經提出了幾種GNN變體來解決上述問題。 但是，他們不是這篇文章的重點。

DeepWalk

DeepWalk是第一個以無監督學習的節點嵌入算法。 它在訓練過程中類似于詞嵌入。 它的初衷是圖中的兩個節點分布和語料庫中的單詞分布都遵循冪律，如下圖所示：

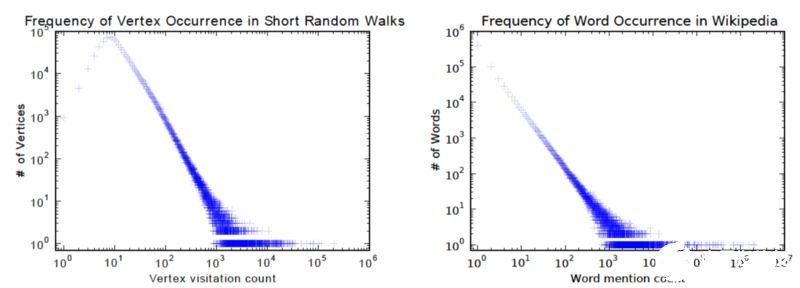
http://www.perozzi.net/publications/14_kdd_deepwalk.pdf

算法包括兩個步驟：

在圖中的節點上執行隨機游走生成節點序列

運行skip-gram，根據步驟1中生成的節點序列學習每個節點的嵌入

在隨機游走過程中，下一個節點是從前一節點的鄰居統一采樣。 然后將每個序列截短為長度為2 | w |+1的子序列，其中w表示skip-gram中的窗口大小。如果您不熟悉skip-gram，我之前的博客文章已經向您介紹它的工作原理。

在論文中，分層softmax用于解決由于節點數量龐大而導致的softmax計算成本過高的問題。為了計算每個單獨輸出元素的softmax值，我們必須為所有元素k計算ek。

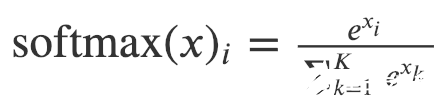
softmax的定義

因此，原始softmax的計算時間是 O（|V|） ，其中其中V表示圖中的頂點集。

多層的softmax利用二叉樹來解決softmax計算成本問題。 在二叉樹中，所有葉子節點（上面所說的圖中的v1，v2，。.. v8）都是圖中的頂點。 在每個內部節點中（除了葉子節點以外的節點，也就是分枝結點），都通過一個二元分類器來決定路徑的選取。 為了計算某個頂點v_k的概率，可以簡單地計算沿著從根節點到葉子節點v_k的路徑中的每個子路徑的概率。 由于每個節點的孩子節點的概率和為1，因此在多層softmax中，所有頂點的概率之和等于1的特性仍然能夠保持。如果n是葉子的數量，二叉樹的最長路徑由O（log（n））限定，因此，元素的計算時間復雜度將減少到O（log | V |）。

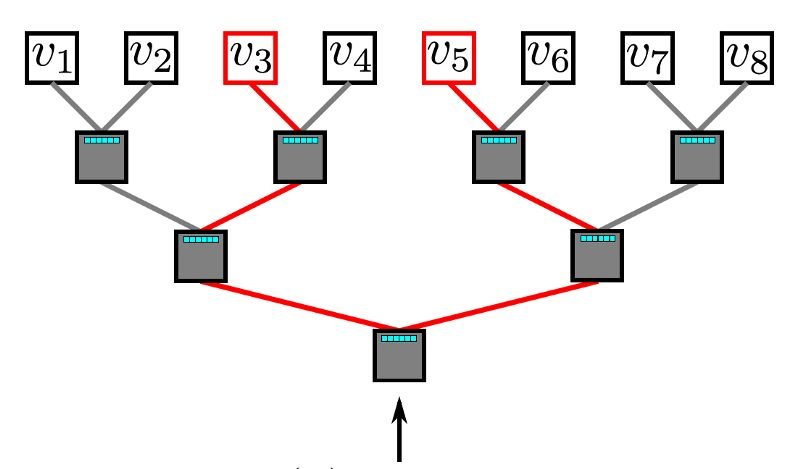
多層softmax

（http://www.perozzi.net/publications/14_kdd_deepwalk.pdf）

在訓練DeepWalk GNN之后，模型已經學習到了了每個節點的良好表示，如下圖所示。 不同的顏色在輸入圖中（圖a）表示不同標簽。 我們可以看到，在輸出圖（每個頂點被嵌入到2維平面）中，具有相同標簽的節點聚集在一起，而具有不同標簽的大多數節點被正確分開。

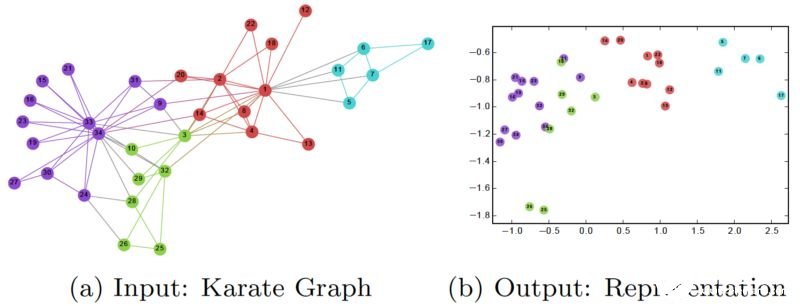
http://www.perozzi.net/publications/14_kdd_deepwalk.pdf

然而，DeepWalk的主要問題是它缺乏泛化能力。 每當有新節點加入到圖中時，它必須重新訓練模型以正確表示該節點（ 直推式學習 ）。 因此，這種GNN不適用于圖中節點不斷變化的動態圖。

GraphSage

GraphSage提供了解決上述問題的解決方案，它以歸納方式學習每個節點的嵌入。 具體來講，它將每個節點用其鄰域的聚合重新表示。 因此，即使在訓練時間期間未出現在圖中新節點，也仍然可以由其相鄰節點正確地表示。 下圖展示了GraphSage的算法過程。

https://www-cs-faculty.stanford.edu/people/jure/pubs/graphsage-nips17.pdf

外層for循環表示更新迭代次數，而 h^k_v 表示節點v 在迭代第 k 次時的本征向量。 在每次迭代時，將通過聚合函數，前一次迭代中 v 和 v 領域的本征向量以及權重矩陣W^k 來更新h^k_v 。這篇論文提出了三種聚合函數：

1.均值聚合器：

均值聚合器取一個節點及其鄰域的本征向量的平均值。

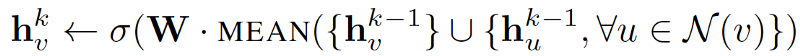
https://www-cs-faculty.stanford.edu/people/jure/pubs/graphsage-nips17.pdf

與原始方程相比，它刪除了上述偽代碼中第5行的連接操作。 這種操作可以被視為“skip-connection” （“跳連接”），這篇論文后面將證明其可以在很大程度上提高模型的性能。

2. LSTM聚合器：

由于圖中的節點沒有任何順序，因此他們通過互換這些節點來隨機分配順序。

3.池聚合器：

此運算符在相鄰頂點集上執行逐元素池化函數。下面顯示了最大池的例子：

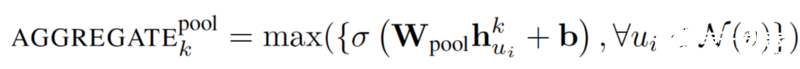
https://www-cs-faculty.stanford.edu/people/jure/pubs/graphsage-nips17.pdf

可以用平均池或任何其他對稱池函數替換這種最大池函數。盡管均值池和最大池聚合器性能相似，但是池聚合器（也就是說采用最大池函數）被實驗證明有最佳的性能。 這篇論文使用max-pooling作為默認聚合函數

損失函數定義如下：

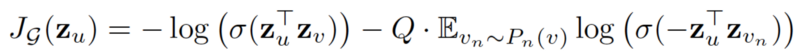
https://www-cs-faculty.stanford.edu/people/jure/pubs/graphsage-nips17.pdf

其中u 和v 共同出現在一定長度的隨機游走中，而 v_n 是不與u共同出現的負樣本。這種損失函數鼓動節點在投影空間中更靠近嵌入距離更近的節點，而與那些相距很遠的節點分離。通過這種方法，節點將獲得越來越多其鄰域的信息。

GraphSage通過聚合其附近的節點，可以為看不見的節點生成可表示的嵌入位置。它讓節點嵌入的方式可以被應用于涉及動態圖的研究領域，這類動態圖的圖的結構是可以不斷變化的。例如，Pinterest采用了GraphSage的擴展版本PinSage作為他們的內容探索系統的核心。

結束語

您已經學習了圖形神經網絡，DeepWalk和GraphSage的基礎知識。 GNN在復雜圖形結構建模中的強大功能確實令人驚訝。鑒于其高效性，我相信GNN將在人工智能的發展中發揮重要作用。如果您覺得我的文章還不錯，請不要忘記在Medium和Twitter上關注我，我經常分享AI，ML和DL的高級發展動態。