一、概述

背包問題是一類比較特殊的動態規劃問題，這篇文章的側重點會在答案的推導過程上，我們還是會使用之前提到的解動態規劃問題的四個步驟來思考這類問題。

在講述背包問題之前，首先提及一下，背包類動態規劃問題和其他的動態規劃問題的不同之處在于，背包類動態規劃問題會選用值來作為動態規劃的狀態，你可以回顧下之前我們討論過的動態規劃問題，基本上都是利用數組或者是字符串的下標來表示動態規劃的狀態。

針對背包類問題，我們依然可以畫表格來輔助我們思考問題，但是背包類問題有基本的雛形，題目特征特別明顯，當你理解了這類問題的解法后，遇到類似問題基本上不需要額外的輔助就可以給出大致的解法，這也就是說，學習背包類問題是一個性價比很高的事情，理解了一個特定問題的解法，基本上一類問題都可以直接套這個解法。

二、問題雛形

首先我們來看看這樣一個問題：

有 N 件物品和一個容量為 V 的背包。第 i 件物品的體積是 C[i]，價值是 W[i]。求解將哪些物品裝入背包可使價值總和最大。求出最大總價值

話不多說，我們還是按之前的分析四步驟來看看這個問題：

問題拆解

我們要求解的問題是 “背包能裝入物品的最大價值”，這個問題的結果受到兩個因素的影響，就是背包的大小，以及物品的屬性（包括大小和價值）。對于物品來說，只有兩種結果，放入背包以及不放入背包，這里我們用一個例子來畫畫表格：

假設背包的大小是 10，有 4 個物品，體積分別是 [2,3,5,7]，價值分別是 [2,5,2,5]。

1、如果我們僅考慮將前一個物品放入背包，只要背包體積大于 2，此時都可以獲得價值為 2 的最大價值：

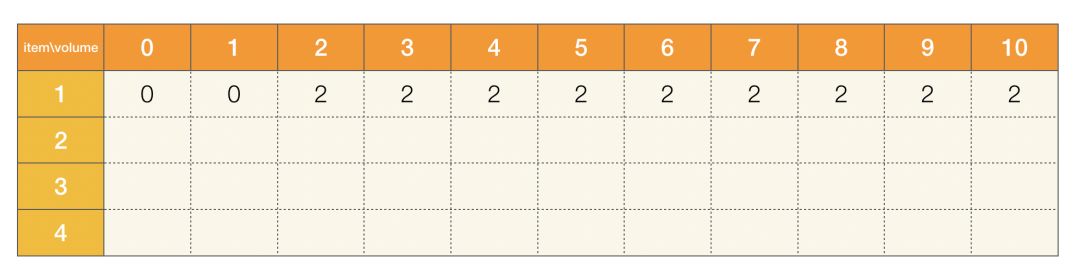
圖一

2、如果我們僅考慮將前兩個物品放入背包，如果背包體積大于或等于 5，表示兩個物體都可放入，此時都可以獲得價值為 2+5=7 的最大價值，如果不能全都放入，那就要選擇體積不超，價值最大的那個：

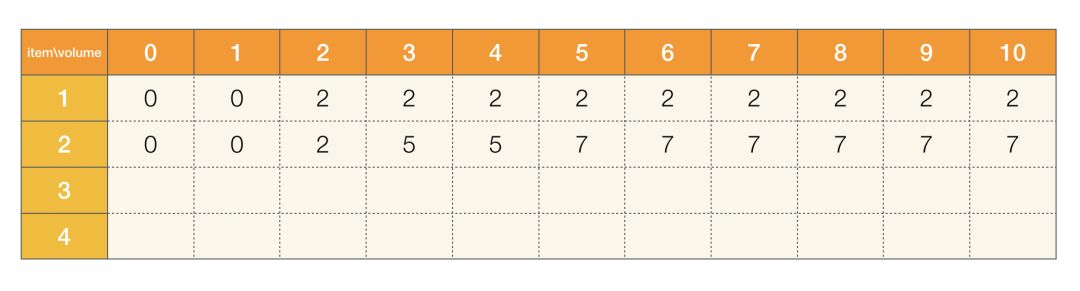
圖二

3、如果我們僅考慮將前三個物品放入背包，如果背包體積大于或等于 10，表示三個物體都可放入，此時都可以獲得價值為 2+5+2=9 的最大價值，如果不能全都放入，那就要選擇體積不超，價值最大的那個方案：

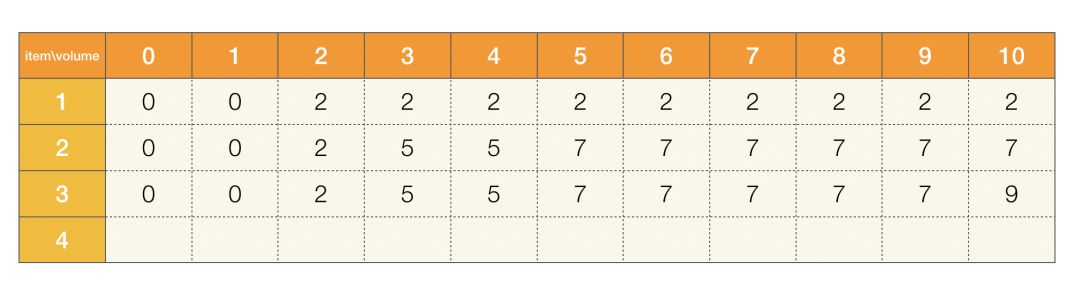
圖三

4、如果我們考慮將所有物品放入背包，我們可以依據前三個物品放入的結果來制定方案：

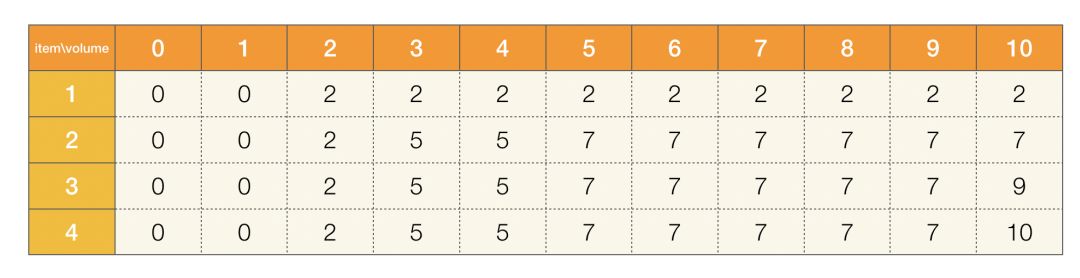
圖四

這樣，我們就根據物品和體積將問題拆分成子問題，也就是 “前 n 個物品在體積 V 處的最大價值” 可以由 “前 n - 1 個物品的情況” 推導得到。

狀態定義

在問題拆解中，我們得知問題其實和背包的體積還有當前考慮的物品有關，因此我們可以定義dp[i][j]表示 “考慮將前 i 個物品放入體積為 j 的背包里所獲得的最大價值”

遞推方程

當我們考慮是否將第 i 個物品放入背包的時候，這里有兩種情況

不放入，也就是不考慮第 i 個物品，那么問題就直接變成了上一個子問題，也就是考慮將 i - 1 個物品放入背包中，這樣當前問題的解就是之前問題的解：

dp[i][j]=dp[i-1][j]

如果背包體積大于第 i 個物品的體積，我們可以考慮將第 i 個物品放入，這個時候我們要和之前的狀態做一個比較，選取最大的方案：

dp[i][j]=Math.max(dp[i-1][j],dp[i-1][j-C[i]]+W[i])

實現

實現這一環節還是主要考慮狀態數組如何初始化，你可以看到，我們每次都要考慮 i - 1，另外還要考慮背包體積為 0 的情況，因此初始化數組時多開一格可以省去不必要的麻煩

publicintzeroOnePack(intV,int[]C,int[]W){ //防止無效輸入 if((V<=?0)?||?(C.length?!=?W.length))?{ ????????return?0; ????} ????int?n?=?C.length; ????//?dp[i][j]:?對于下標為?0～i?的物品，背包容量為?j?時的最大價值 ????int[][]?dp?=?new?int[n?+?1][V?+?1]; ????//?背包空的情況下，價值為?0 ????dp[0][0]?=?0; ????for?(int?i?=?1;?i?<=?n;?++i)?{ ????????for?(int?j?=?1;?j?<=?V;?++j)?{ ????????????//?不選物品?i?的話，當前價值就是取到前一個物品的最大價值，也就是?dp[i?-?1][j] ????????????dp[i][j]?=?dp[i?-?1][j]; ????????????//?如果選擇物品?i?使得當前價值相對不選更大，那就選取?i，更新當前最大價值 ????????????if?((j?>=C[i-1])&&(dp[i][j]

這里還有一個空間上面的優化，如果你回到我們之前畫的表格，考慮前 i 個問題的狀態只會依賴于前 i - 1 個問題的狀態，也就是dp[i][...]只會依賴于dp[i - 1][...]，另外一點就是當前考慮的背包體積只會用到比其小的體積。

基于這些信息，我們狀態數組的維度可以少開一維，但是遍歷的方向上需要從后往前遍歷，從而保證子問題需要用到的數據不被覆蓋，優化版本如下：

publicintzeroOnePackOpt(intV,int[]C,int[]W){ //防止無效輸入 if((V<=?0)?||?(C.length?!=?W.length))?{ ????????return?0; ????} ????int?n?=?C.length; ????int[]?dp?=?new?int[V?+?1]; ????//?背包空的情況下，價值為?0 ????dp[0]?=?0; ????for?(int?i?=?0;?i?=C[i];--j){ dp[j]=Math.max(dp[j],dp[j-C[i]]+W[i]); } } returndp[V]; }

這里，因為物品只能被選中 1 次，或者被選中 0 次，因此我們稱這種背包問題為01 背包問題。

還有一類背包問題，物品可以被選多次或者 0 次，這類問題我們稱為完全背包問題，這類背包問題和 01 背包問題很類似，略微的不同在于，在完全背包問題中，狀態dp[i][j]依賴的是dp[i - 1][j]以及dp[i][k] k < j，你可以看看下面的實現代碼：

publicintcompletePack(intV,int[]C,int[]W){ //防止無效輸入 if(V==0||C.length!=W.length){ return0; } intn=C.length; //dp[i][j]:對于下標為0～i的物品，背包容量為j時的最大價值 int[][]dp=newint[n+1][V+1]; //背包空的情況下，價值為0 dp[0][0]=0; for(inti=1;i<=?n;?++i)?{ ????????for?(int?j?=?1;?j?<=?V;?++j)?{ ????????????//?不取該物品 ????????????dp[i][j]?=?dp[i?-?1][j]; ????????????//?取該物品，但是是在考慮過或者取過該物品的基礎之上(dp[i][...])取 ????????????//?0-1背包則是在還沒有考慮過該物品的基礎之上(dp[i?-?1][...])取 ????????????if?((j?>=C[i-1])&&(dp[i][j-C[i-1]]+W[i-1]>dp[i][j])){ dp[i][j]=dp[i][j-C[i-1]]+W[i-1]; } } } //返回，對于所有物品（0～N），背包容量為V時的最大價值 returndp[n][V]; }

類似的，我們還是可以對狀態數組進行空間優化，依據我們之前討論的狀態之間的依賴關系，完全背包的空間優化我們直接把狀態數組少開一維即可，遍歷方式都不需要改變：

publicintcompletePackOpt(intV,int[]C,int[]W){ if(V==0||C.length!=W.length){ return0; } intn=C.length; int[]dp=newint[V+1]; for(inti=0;i

下面，我們就根據這兩類背包問題，看看遇到類似的問題我們是否可以套用上面我們介紹的解法。

三、相關題目實戰

LeetCode 第 416 號問題：分割等和子集。

題目來源：https://leetcode-cn.com/problems/partition-equal-subset-sum/

題目描述

給定一個只包含正整數的非空數組。是否可以將這個數組分割成兩個子集，使得兩個子集的元素和相等。

注意:

每個數組中的元素不會超過 100

數組的大小不會超過 200

示例 1:

輸入:[1,5,11,5] 輸出:true 解釋:數組可以分割成[1,5,5]和[11].

示例 2:

輸入:[1,2,3,5] 輸出:false 解釋:數組不能分割成兩個元素和相等的子集.

題目分析

題目給定一個數組，問是否可以將數組拆分成兩份，并且兩份的值相等，這里并不是說分成兩個子數組，而是分成兩個子集。

直觀的想法是直接遍歷一遍數組，這樣我們可以得到數組中所有元素的和，這個和必須是偶數，不然沒法分，其實很自然地就可以想到，我們要從數組中挑出一些元素，使這些元素的和等于原數組中元素總和的一半，“從數組中找出一些元素讓它們的和等于一個固定的值”，這么一個信息能否讓你想到背包類動態規劃呢？

如果你能想到這個地方，再配上我們之前講的01 背包問題的解法，那么這道題目就可以直接套解法了，這里我就不具體分析了。

參考代碼

publicbooleancanPartition(int[]nums){ if(nums==null||nums.length==0){ returnfalse; } intsum=0; intn=nums.length; for(inti=0;i=nums[i];--j){ dp[j]|=dp[j-nums[i]]; } } returndp[target]; }

LeetCode 第 322 號問題：零錢兌換。

題目來源：https://leetcode-cn.com/problems/coin-change

題目描述

給定不同面額的硬幣coins和一個總金額amount。編寫一個函數來計算可以湊成總金額所需的最少的硬幣個數。如果沒有任何一種硬幣組合能組成總金額，返回-1。

示例 1:

輸入:coins=[1,2,5],amount=11 輸出:3 解釋:11=5+5+1

示例 2:

輸入:coins=[2],amount=3 輸出:-1

說明:
你可以認為每種硬幣的數量是無限的。

題目分析

題目給定一個數組和一個整數，數組里面的值表示的是每個硬幣的價值，整數表示的是一個價值，問最少選擇多少個硬幣能夠組成這個價值，硬幣可以重復選擇。

雖然這里只有一個輸入數組，但是我們還是可以看到背包的影子，這里的整數就可以看作是背包的體積，然后數組里面的值可以看作是物品的體積，那物品的價值呢？

在這里，你可以形象地認為每個物品的價值是 1，最后我們要求的是填滿背包的最小價值，因為這里物品是可以重復選擇多次的，因此可以歸類于完全背包問題，套用之前的解法就可以解題，唯一要注意的一點是，這里我們不在求最大價值，而求的是最小價值，因此我們需要先將狀態數組初始化成無窮大。

參考代碼

publicintcoinChange(int[]coins,intamount){ int[]dp=newint[amount+1]; Arrays.fill(dp,Integer.MAX_VALUE); dp[0]=0; for(inti=0;i

輔助動畫

LeetCode 第 518 號問題：零錢兌換II。

題目來源：https://leetcode-cn.com/problems/coin-change-2/

題目描述

給定不同面額的硬幣和一個總金額。寫出函數來計算可以湊成總金額的硬幣組合數。假設每一種面額的硬幣有無限個。

示例 1:

輸入:amount=5,coins=[1,2,5] 輸出:4 解釋:有四種方式可以湊成總金額: 5=5 5=2+2+1 5=2+1+1+1 5=1+1+1+1+1

示例 2:

輸入:amount=3,coins=[2] 輸出:0 解釋:只用面額2的硬幣不能湊成總金額3。

示例 3:

輸入:amount=10,coins=[10] 輸出:1

注意:

你可以假設：

0 <= amount (總金額) <= 5000

1 <= coin (硬幣面額) <= 5000

硬幣種類不超過 500 種

結果符合 32 位符號整數

題目分析

這道題目是上一道題目的變形，題目的輸入參數還是不變，變的是最后的問題，這里需要求的是 “有多少種組合方式能夠填滿背包”，我們還是可以套用完全背包的解法，只是最后求解的東西變了，那我們動態規劃狀態數組中記錄的東西相應的改變即可，在這道題中，狀態數組中記錄組合成該價值的方案的個數即可。

參考代碼

publicintchange(intamount,int[]coins){ int[]dp=newint[amount+1]; dp[0]=1; for(inti=0;i

K Sum。

題目描述

給定一個輸入數組 array，還有兩個整數 k 和 target，在數組 array 中找出 k 個元素，使得這 k 個元素相加等于 target，問有多少種組合方式，輸出組合方式的個數。

注：在一種組合方式中，一個元素不能夠被重復選擇

題目分析

我們之前講過 Two Sum，也提到過 3 Sum，還有 4 Sum，那這道題是否可以套用之前的解法呢？

這里有一個細節不知道你是否發現，就是這道題目僅僅是讓你輸出所有組合方式的個數，并沒有讓你輸出所有的組合方式，這是決定是否使用動態規劃很重要的一點。

如果沒有這個 k，我相信你會很直接地想到使用01 背包問題的解法，那我們可以思考一下，基于原來的解法，如果增加了 k 這個限制，我們需要額外做些什么事情呢？

因為 k 會決定問題的狀態，因此我們的狀態數組中也要考慮 k，在考慮將第 k 個元素放入背包中，我們需要看的是背包中存放 k - 1 個元素的情況，這么看來，其實相比普通的01 背包問題，這道題目僅僅是增加了一維狀態，沒有其他的變化。

參考代碼

publicintkSum(int[]array,intk,inttarget){ int[][]dp=newint[target+1][k+1]; dp[0][0]=1; for(inti=0;i=array[i];--j){ //和普通01背包問題相比，僅僅是多了一層狀態需要考慮 //這層狀態記錄的是背包里面元素的個數 //我們放入第r個元素的時候，必須確保背包里面已經有r-1個元素 for(intr=1;r<=?k;?++r)?{ ????????????????dp[j][r]?+=?dp[j?-?array[i]][r?-?1]; ????????????} ????????} ????} ????return?dp[target][k]; }

四、總結

背包類的動態規劃問題我們就先講到這里，我們介紹了兩類比較基礎的背包問題，01 背包問題和完全背包問題，解這類問題有既定的模版和思路可以參照，理解了模版問題，也就理解了一類問題，算是學習性價比很高的一類動態規劃問題。

往往背包類問題可以很好地根據題目的描述判斷出來，這類問題狀態的定義也比較特殊，就是用值來作為動態規劃的狀態，我們也用了一些習題來練習了一番，相信你對背包問題有了大致的了解，也對動態規劃有了更廣的認識。