半個世紀前固體能帶理論的提出,讓人們認識到材料為什么可以分為金屬、絕緣體或者半導體,并促進了半導體產業的迅猛發展。現在人們認識到,系統的能帶還可以根據對稱性和空間維度,進行詳細的拓撲分類。例如,考慮時間反演對稱性、粒子-空穴對稱性、手征對稱性,以及不同的空間維度(d),絕緣態系統可以衍生出種類豐富的拓撲物態(見下表)。
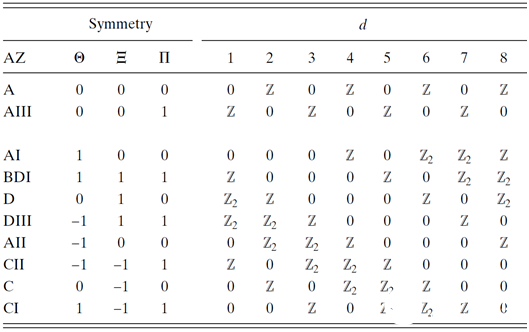
按照對稱性和空間維度可對具有能隙的物態進行拓撲分類
拓撲材料具有拓撲保護的物理性質,不受雜質、缺陷等因素的影響,因而在低能耗、高速響應器件,量子計算等領域中具有巨大的潛在應用,在近十多年來受到了非常廣泛的研究。人們已經在天然材料和人工材料中提出和驗證了多種一維到三維的拓撲物態。例如,在破缺時間反演對稱性(表中A類)的二維系統中,克勞斯·馮·克利青發現了整數量子霍爾態;在具備時間反演對稱性的費米子系統中(表中AII類),人們發現了二維或者三維的拓撲絕緣態;考慮粒子-空穴對稱性后可以出現一維到三維的拓撲超導態等。
我們生活的世界是三維空間,難以制備維度高于三維的材料系統,因此目前對高維度拓撲物態的研究還非常匱乏。
相比于天然材料,人工系統,特別是電路系統,具有若干優點。例如,系統的能帶可以被精確設計和調控;系統具有自由的格點連通性,可以用來模擬任意維度的連接。因此,電路系統為實現有趣的高維拓撲物態提供了理想的實驗平臺。
近期,武漢大學余睿、南京大學趙宇心和斯圖加特馬克斯-普朗克研究所的Andreas Schnyder利用電路連接自由度高、不受空間維度制約的特性,用電容和電感器件構建了一個具有四維連接性質、滿足經典時間反演對稱的電路網絡(如下圖)。
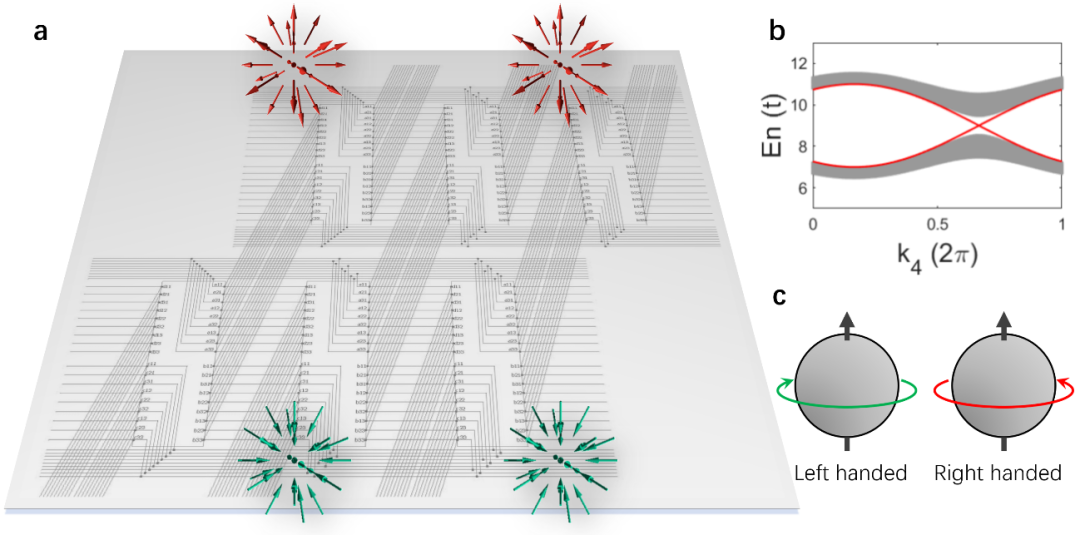
(a)四維電路投影到二維電路板上。其三維邊界上可以存在一對手性相同的外爾點。(b)三維邊界上體態(灰色部分)和外爾點的色散(紅色部分)。(c) 外爾點手性示意圖。
通過理論分析,研究者證明此系統屬于上表中AI分類的四維拓撲絕緣態。拓撲絕緣體是一種很特殊的材料:系統體內絕緣,但表面因為存在拓撲保護的、無能隙的表面態而具備高度導電性。類似的,對于具有四維拓撲絕緣態性質的電路網絡,其體內頻譜具有能隙,但其三維表面上存在一對符合三維Weyl態特征的能隙閉合點(上圖b)。
更重要的是,這種特殊的表面態起源于四維空間的拓撲數——第二陳數。拓撲數確定了Weyl態必須成對出現在邊界上且具有相同的手征(上圖a),即它們的內稟旋轉自由度和傳播方向遵循相同的左手或右手定則(上圖c)。這些性質和低維材料中的表面態性質有很大不同。
研究人員通過電路仿真指出,這種四維拓撲態能夠在電路板或集成電路晶圓上實現;系統表面的三維Weyl態的性質可通過電路節點電壓表征和操控。
上述設計方案具有普適性,可用于實現任意維度的其它類型的拓撲物態,且這種方案具有實現簡單、重構性強、可靈活控制等優點。研究人員期望該方案能夠在拓撲相變、非線性效應、高維物態、非平衡現象以及開放量子系統(非厄密系統)的研究中起到重要作用。
該研究得到了科技部科研項目和國家自然科學基金的資助,相關成果發表于《國家科學評論》(National Science Review)。
責任編輯:pj
-
拓撲
+關注
關注
4文章
346瀏覽量
29979 -
絕緣
+關注
關注
1文章
450瀏覽量
22289
發布評論請先 登錄
通過交互式對稱性校驗提升集成電路設計流程
以低噪聲實現降壓-升壓電壓轉換
風華貼片電感的標準分類體系

一文講清楚芯片的分類-多個維度
一種分段氣隙的CLLC變換器平面變壓器設計
半導體新發現:拓撲激子密度波量子物態

激光自身空間維度加工系統綜述

如何使用ddc進行數據分類
飛虹MOS管FHP1906V在全橋拓撲電路中的應用




















評論