一種基于 Bayer 型圖像數據的自適應非局部均值濾波算法
針對非局部均值降噪算法在 Bayer 型圖像數據上的應用優化,提出一種自適應平滑系數優化算法。基于當前局部均方差以及均值的比值確定噪聲系數,根據噪聲系數確定劃分區域,自適應調整非局部均值降噪的平滑系數,提高紋理區域的細節表現。同時融合 LOG 變換之后的降噪優化數據,提高圖像中暗部區域的降噪表現。此優化算法較傳統的非局部均值算法在主觀體驗上有較大的改善。
一種基于Bayer型圖像數據的自適應非局部均值濾波算法。集成電路應用, 2020, 37(04): 13-15.
An Adaptive Non-local Mean Filtering Algorithm
Based on Bayer Image Data
WANG Yong, LI Yunsheng
Abstract — In order to optimize the application of non-local means denoising algorithm in Bayer image data, propose an adaptive smoothing coefficient optimization algorithm.Based on the ratio of the local mean square deviation and the mean value to determine the noise coefficient and the partition area determined by the noise coefficient, the smoothing coefficient of non-local mean noise reduction is adaptively adjusted to improve the detail performance of the texture region.At the same time, the optimized data of noise reduction after log transform is fused to improve the performance of noise reduction in the dark area of the image.Compared with the traditional non-local mean algorithm, this optimization algorithm has a greater improvement in subjective experience.
Index Terms — image denoising, bayer image data, non-local mean, adaptive.
圖像降噪技術是數字圖像處理領域的基礎技術之一。在整個圖像信號處理(Image Signal Processing,ISP)流程中,在后端處理降噪,圖像噪聲的性質會變得更加復雜,增加更多的結構性、彩色噪聲以及給噪聲帶來非線性的變化,所以越來越傾向于在 ISP 前端進行降噪處理。經典的降噪方法包含:均值濾波、中值濾波、高斯濾波、維納濾波等,傳統的空域去噪算法是基于單個像素的相似性例如雙邊濾波,不能很好地保留邊緣和紋理細節,后來 2005 年 Buades 等根據圖像局部的相似性,提出了 NLM 降噪算法(Non-local Means Denoising Algorithm),相對于單個像素更好的表達了圖像的結構。之后學者們還有提出基于圖像塊的相似性匹配然后進行 3D 濾波概念的 BM3D 算法(Block-Matching and 3D filtering),但是由于 BM3D 算法所需要的資源特別龐大,在實時處理上會有一定的難度,所以在視頻流的 Bayer 型圖像數據降噪處理上還是以 NLM 算法為主。
NLM 算法雖然取得了不錯的降噪效果,但是在參數h的設定上不明確,當噪聲水平較強時,對于同一參數 h 可能會存在某些部分過于模糊的情況,對于 ISP 后期的處理帶來不便。本文根據圖像局部的噪聲系數,并結合噪聲域非局部均值算法中濾波參數的關系,自適應地獲取濾波參數,同時與 LOG 域算法相結合,提高了算法效果。
1 非局部圖像算法
假定噪聲圖像為式(1)。
F={ F(i)│i∈A } (1)
其中,A 為區域,F(i)為當前圖像的像素值,f(i)為濾波后的像素值,NLM 算法表示為式(2)~式(4)。
其中,a 為高斯核函數的標準差;N(i)為以 i 為中心的圖像;d(i,j) 為以 i 為中心和以 j 為中心兩個圖像塊的相似距離,一般是表示為歐氏距離;w(i,j) 為兩個圖像塊之間的融合權重,表示兩個圖像塊之間的相似程度;I 代表以 i 為中心的搜索范圍; h 為平滑參數,控制降噪程度的系數;h 越大,越平滑。
2 改進的非局部均值濾波算法
針對非局部均值濾波算法的不足,本文提出一種自適應的且與 LOG 域算法相結合的非局部均值濾波算法。首先圖像轉化為 LOG 域,根據搜索框內的局部方差判斷出原始圖像以及 LOG 變換后圖像的降噪系數h的選擇范圍,同時對 h 有所限制。然后調整完之后根據降噪的平滑程度來進行原始圖像降噪以及 LOG 變換后降噪的權重融合,此方法能夠有效地改善圖像質量。
2.1 LOG 變換
LOG 變換主要用于將圖像的低灰度值部分擴展,將其高灰度值部分壓縮,以達到強調圖像低灰度部分的目的,如式(5)。
s=log(1+F(i))/z(5)
這里的 F(i) 代表的是 Bayer 型圖像數據的像素值,如果是 12 bit 像素位寬,則 F(i)∈[0,4 095];z 是歸一化系數,對于 12 bit 數據,z 的值為8.3178。
將原始 Bayer 型圖像 LOG 變換之后能夠凸顯暗部的噪聲,再進行降噪處理后,與原始 Bayer 型圖像融合的同時能夠兼顧暗部的噪聲水平以及紋理表現。
2.2 平滑參數h的自適應變化
平滑參數的自適應變化主要依據局部的噪聲系數來確定。
局部的噪聲系數主要是依靠局部的均方差與均值的比值確定,注意局部評估是不區分 Bayer R/G/B 通道情況,整體評估,如式(6)。
CoefNoise 是噪聲系數,I 是領域搜索框,Num 是搜索框中的參與的數目個數。F(j)是位置為 j 的點的像素值,a 是噪聲系數的調整幅度。
根據文獻[6]可以得到平滑系數 h=3.3×σ2,σ是圖像的標準差。在 Bayer 域因為噪聲的表現與圖像的亮度相關,所以 CoefNoise 的大小是用局部的均方差以及亮度均值的比值來確定,劃分出平緩區域,過渡區域以及高頻區域,如式(7)。
sigmaMax 以及 sigmaMin 是給自適應平滑系數規定的最大與最小值;sigmaMax 大于等于sigmaMin;sigmaMax 是影響高頻部分清晰度,sigmaMax 增大,高頻部分越平滑;sigmaMin 是影響平坦區域的降噪程度,sigmaMin 增大,平坦區域降噪程度越高。當 sigmaMax 以及 sigmaMin 為固定值時,a 影響整體降噪強度,a 增大,高頻區域增多, a 減小,高頻區域減少。
2.3 融合系數
LOG 域變換降噪之后需要與原始 Bayer 型圖像進行融合,由于 LOG 變化之后主要對暗部區域進行處理,對于亮部區域的經過 LOG 變換之后像素區域都接近飽和,局部標準差比較小,所以只有 LOG 變換之后只有在條件 CofNoise>beta×sigmaMax 下才進行融合,beta 作為確定暗部區域的系數,一般選取 0.95。融合過程為式(8)。
其中,output(i) 是輸出像素值,betaMix 是融合系數,一般是 0.5;f(i) 是正常 Bayer 圖像降噪之后的像素值,flog(i) 是經過 LOG 變換之后降噪的像素值。
3 實驗結果與分析
實驗過程中,由于考慮到在實際應用上運算量的問題,采用相似窗大小為 9×9,搜索框大小 3×3。實驗中選取的測試圖片為采集得到的真實帶噪聲的 Bayer 數據圖片,圖像大小為 496×728。由于 NLM 是業內公認效果較好的降噪算法,所以對比的圖像測試效果是與常規 NLM 以及優化后的算法效果對比。
為原始 Bayer 型圖像帶噪聲數據與經過 Demosaic/AWB/Gamma 之后的 RGB 圖像, 為原始 Bayer 型圖像 GroudTruth 數據(不帶噪聲)與 為經過Demosaic/AWB/Gamma之后的RGB圖像。為了更直觀地展現效果,接著的圖片是展現經過 Demosaic/AWB/Gamma 之后的效果。
3.1 去噪效果對比的主觀表現
為場景一的主觀效果圖, 為場景二的主觀效果圖。優化后的算法較之前常規 NLM 的算法有較好的視覺效果,在暗部區域以及紋理區域能夠較好地保持細節,為了能夠更好地展示效果,以及 把局部細節放大后顯示。
由于優化后的算法根據局部的噪聲系數確定不同區間的平滑參數,通過最小噪聲系數限制平滑區域的降噪強度,避免平滑區域雖然噪聲較多,但是噪聲系數仍然較低降噪不完全的情況;通過最大噪聲系數限制強邊緣區域的降噪強度,避免強邊緣區域降噪強度過高,過渡區域(最小噪聲系數和最大噪聲系數之間)能夠自適應調節平滑系數。同時由于 Bayer 數據像素亮度較低,通過 LOG 變換后的降噪處理與變換前的降噪處理數據融合,能夠優化暗部區域的噪聲水平,為后端的 Gamma 變換/色調映射等算法提供支持。從以及 可以看出平坦區域和強邊緣區域基本保持一致,從 中能夠明顯看出細節部分有明顯的增強,符合在 Bayer 型圖像數據降噪的時候保持住足夠的紋理信息,為后端算法處理留有空間的目的。
3.2 去噪效果對比的數據表現(峰值信噪比 PSNR 與信噪比 SNR)
為了進一步確認優化后算法優勢,本文增加兩組數據的峰值信噪比(PSNR)和信噪比(SNR)對比來說明去噪效果,即采集同一場景的 60 幀數據,取平均合成了 GroundTruth 圖片作為無噪聲圖像,進行對比。
可以看出,優化后的算法在 PSNR、SNR 上都優于經典的 NLM 算法。由于主要的優化區域是噪聲系數過渡區域(最小噪聲系數和最大噪聲系數之間)以及暗部區域,SNR 以及 PSNR 是整幅圖像對比計算,所以在主觀上有明顯優化,但是從 SNR 以及 PSNR 的數值上不是很明顯。
4 結語
本文提出對于 Bayer 型圖像數據 NLM 降噪算法優化方法,將原來固定的平滑系數值自適應化,結合局部的均方差以及亮度信息,以及 LOG 變換之后對于暗部區域的調整,能夠在原有 NLM 算法基礎上提高細節結構的表現。通過根據真實噪聲的降噪效果展示,優化后的 NLM 降噪算法在細節紋理上有明顯的提升。
責任編輯:pj
-
數據
+關注
關注
8文章
7080瀏覽量
89175 -
圖像降噪
+關注
關注
0文章
7瀏覽量
6700 -
Bayer圖像
+關注
關注
0文章
2瀏覽量
6072
發布評論請先 登錄
相關推薦
傅立葉變換在圖像處理中的作用
AIC3106的底噪如何消除?
求助,請問TLV320AIC3254是否有這樣的抗噪效果?
AIC3104環境底噪是要通過設置寄存器的參數來消除嗎?
TLV320AIC3254輸出聲音的底噪很大是什么原因導致的?
tlv320aic3106底噪過大要如何解決?
運放的反饋電阻習慣性并聯上一個反饋電容,主要目的就是去噪,為什么會起到這種作用?
PGA280噪底很大是為什么?
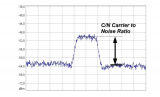
頻譜儀測載噪比怎么測
示波器如何測量底噪?示波器測量底噪的步驟
載噪比和信噪比有什么區別




 去噪效果對比的主觀表現
去噪效果對比的主觀表現










評論