啥是傅立葉級數(shù)？在數(shù)學(xué)中，傅里葉級數(shù)（Fourier series）是把類似波的函數(shù)表示成簡單正弦波的方式。更正式地說法是，它能將任何周期性函數(shù)或周期信號分解成一個（可能由無窮個元素組成的）簡單振蕩函數(shù)的集合，即正弦函數(shù)和余弦函數(shù)（或者，等價地使用復(fù)指數(shù)），從數(shù)學(xué)的定義來看，是這樣地：

設(shè)x（t）是一周期信號，其周期為T。若x（t）在一個周期的能量是有限的，有即

則，可以將x（t）展開為傅立葉級數(shù)。怎么展開呢？計算如下：

公式中的k表示第k次諧波，這是個什么概念呢？不容易理解，看下對于一個方波的前4次諧波合成動圖就比較好理解了。這里的合成的概念是時域上的疊加的概念

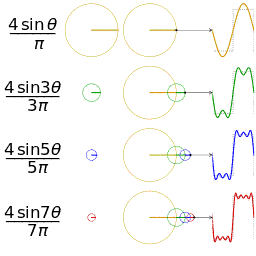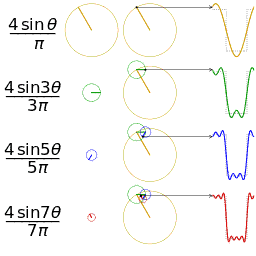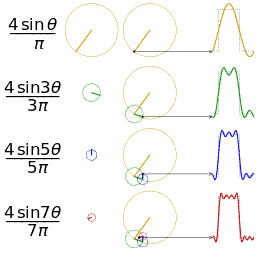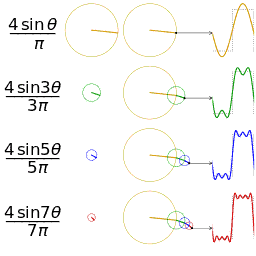
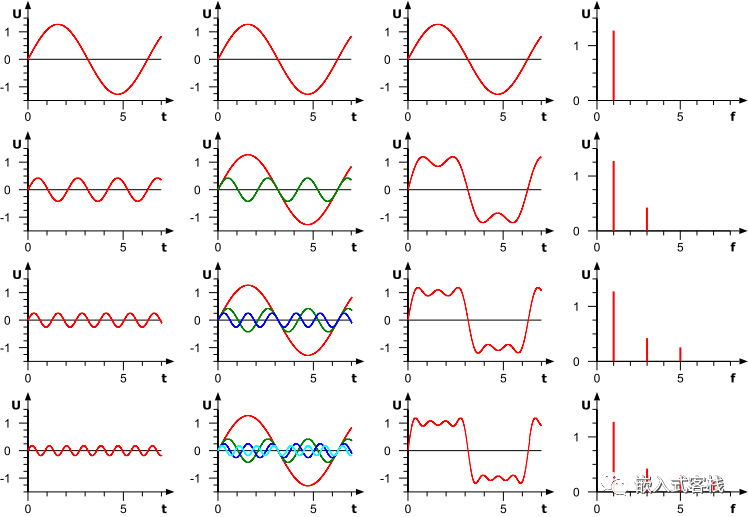
啥是傅里葉變換？在數(shù)學(xué)中，傅里葉變換（Fourier transform FT ）是一種數(shù)學(xué)變換，它將一個函數(shù)（通常是一個時間的函數(shù)，或一個信號）分解成它的組成頻率，例如用組成音符的音量和頻率表示一個音樂和弦。傅里葉變換指的是頻域表示和將頻域表示與時間函數(shù)相關(guān)聯(lián)的數(shù)學(xué)運算。其本質(zhì)是一種線性積分變換，用于信號在時域（或空域）和頻域之間的變換，在物理學(xué)和工程學(xué)中有許多應(yīng)用。因其基本思想首先由法國學(xué)者約瑟夫·傅里葉系統(tǒng)地提出，所以以其名字來命名以示紀念。實際上傅里葉變換就像化學(xué)分析，確定物質(zhì)的基本成分；信號來自自然界，也可對其進行分析，確定其基本頻率成分。其數(shù)學(xué)定義為：

對于連續(xù)時間信號x（t），若x（t）在時間維度上可積分，（實際上并不一定是時間t維度，這里可以是任意維度，只需在對應(yīng)維度空間可積分即可），即：

那么，x（t）的傅立葉變換存在，且其計算式為：

其反變換為：

上面這兩個公式是啥意思呢？在度量空間可積可以理解成其在度量空間能量有限，也即對其自變量積分（相當(dāng)于求面積）是一個確定值，那么這樣的函數(shù)或者信號就可以進行傅立葉變換展開，展開得到的就變成是頻域的函數(shù)了，如果對頻率將函數(shù)值繪制出曲線就是我們所說的頻譜圖，而其反變換就比較好理解了，如果我們知道一個信號或者函數(shù)譜密度函數(shù)，就可以對應(yīng)還原出其時域的函數(shù)，也能繪制出時域的波形圖。

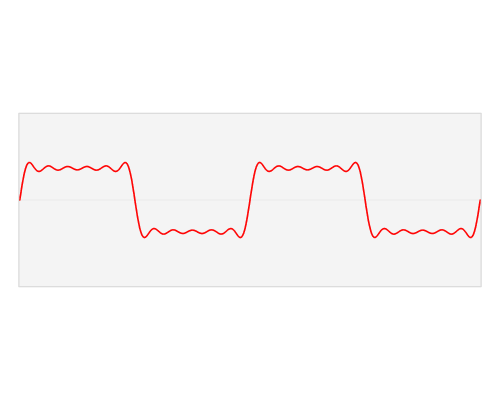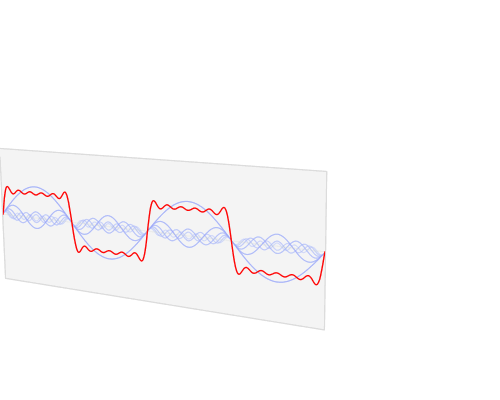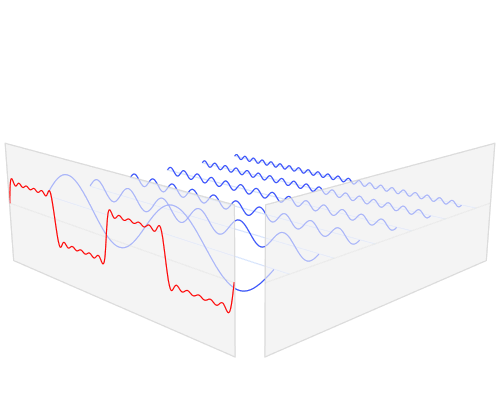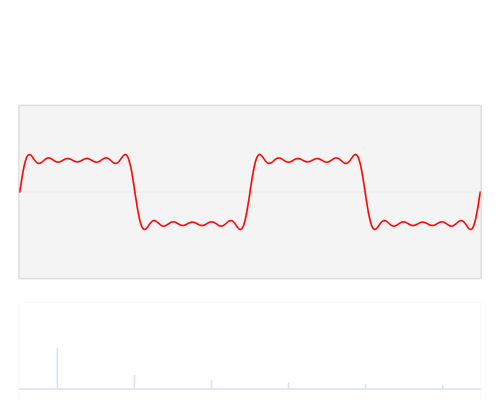
當(dāng)然，本文限定討論時域信號是因為我們電子系統(tǒng)中的應(yīng)用最為普遍的就是一個時域信號，當(dāng)然推而廣之，其他的多維度信號也能利用上面定義進行推廣，同樣在多維空間信號也非常有應(yīng)用價值，比如2維圖像處理等等。

上面兩個概念是一個東東么？傅立葉級數(shù)對應(yīng)的是周期信號，而傅立葉變換則對應(yīng)的是一個時間連續(xù)可積信號（不一定是周期信號）

傅立葉級數(shù)要求信號在一個周期內(nèi)能量有限，而后者則要求在整個區(qū)間能量有限

傅立葉級數(shù)的對應(yīng)是離散的，而傅立葉變換則對應(yīng)是連續(xù)的。

故而，兩者的物理含義不同，且其量綱也是不同的，代表周期信號的第k次諧波幅度的大小，而則是頻譜密度的概念。所以答案是這兩者從本質(zhì)上不是一個概念，傅立葉級數(shù)是周期信號的另一種時域的表達方式，也就是正交級數(shù)，它是不同的頻率的波形的時域疊加。而傅立葉變換則是完全的頻域分析，傅里葉級數(shù)適用于對周期性現(xiàn)象做數(shù)學(xué)上的分析，傅里葉變換可以看作傅里葉級數(shù)的極限形式，也可以看作是對周期現(xiàn)象進行數(shù)學(xué)上的分析，同時也適用于非周期性現(xiàn)象的分析。傅里葉級數(shù)適用于對周期性現(xiàn)象做數(shù)學(xué)上的分析，傅里葉變換可以看作傅里葉級數(shù)的極限形式，也可以看作是對周期現(xiàn)象進行數(shù)學(xué)上的分析，同時也適用于非周期性現(xiàn)象的分析。

啥是離散傅立葉變換？離散傅里葉變換（Discrete Fourier Transform，縮寫為DFT），是傅里葉變換在時域和頻域上都呈離散的形式，將信號的時域采樣變換為其DTFT的頻域采樣。

在形式上，變換兩端（時域和頻域上）的序列是有限長的，而實際上這兩組序列都應(yīng)當(dāng)被認為是離散周期信號的主值序列。即使對有限長的離散信號作DFT，也應(yīng)當(dāng)將其看作其周期延拓的變換。在實際應(yīng)用中通常采用快速傅里葉變換計算DFT。

對于N點序列，它的離散傅立葉變換為（DFT）為：

其中k=0，1，。..。，N-1，上面的式子展開一下：

啥是快速傅立葉變換？快速傅立葉變換（Fast Fourier Transform：FFT）是一種計算數(shù)字信號序列的離散傅立葉變換（Discrete Fourier Transform：DFT）或其逆變換（IDFT）的算法。傅里葉分析將信號從其原始域（通常是時間或空間）轉(zhuǎn)換為頻域的表示，反之亦然。DFT是通過將一系列值分解成不同頻率的分量來獲得的。這個操作在很多領(lǐng)域中都很有用，但是直接從定義中計算它通常太慢而不實際。FFT通過將DFT矩陣分解成稀疏（大部分為零）因子的乘積來快速計算這種轉(zhuǎn)換。所以其本質(zhì)是實現(xiàn)離散傅立葉變換的一種優(yōu)化算法，將時間復(fù)雜度從降低為，其中N為待計算序列的長度。當(dāng)N非常大時，這種優(yōu)化在時間維度上提升是非常顯著的。尤其在嵌入式應(yīng)用領(lǐng)域，由于受限于采用的芯片算力往往不強，所以FFT算法較之于DFT的效果是非常有應(yīng)用價值的。

1994年，Gilbert Strang將FFT描述為“我們一生中最重要的數(shù)值算法”，并被IEEE雜志《計算科學(xué)與工程》列入20世紀十大算法之一，它深遠的影響了我們世界與日常生活。說這個算法改變了世界也不為過。在我們?nèi)粘Ｉ钪泻芏嘣O(shè)備里面都有它的影子，比如手機、比如photoshop，比如數(shù)字音響等等。

快速傅立葉算法的最核心思想就是計算機科學(xué)里面常見的分治思想，即把一個復(fù)雜的問題，分解為一個小的類似問題進行求解。

FFT基本上可分為兩類，時間抽取法和頻率抽取法，而一般的時間抽取法和頻率抽取法只能處理長度N=2M的情況，另外還有組合數(shù)基四FFT來處理一般長度的FFT。所謂抽取，就是把長序列分為短序列的過程，可在時域也可在頻域進行。最常用的時域抽選方法是按奇偶將長序列不斷地變?yōu)槎绦蛄校Y(jié)果使輸入序列為倒序，輸出序列為順序排列，這就是Coolly—Tukey算法。

假定待變換離散時間序列信號長度為，將x（n）按照奇偶分組：

上式可變換為：

令

其中，k取0，1，。..，N/2-1

從而，

由于A（k），B（k）都是點的DFT，X（k）為N點的DFT。那么這一分治思想還可以進一步做下去，這里就不贅述了。

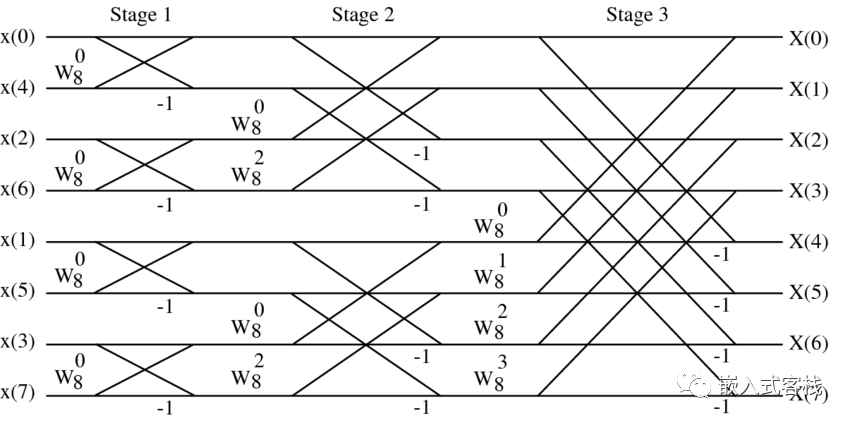
下圖就是一個時間抽取的基2FFT算法的示意圖：

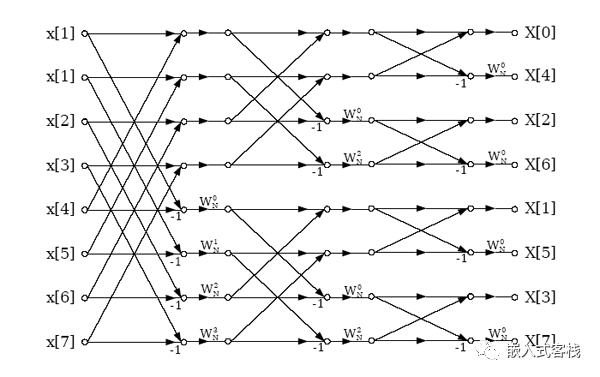
對于頻率抽取基2的示意圖其原理類似，這里放個圖：

不同點：

DIT2 FFT是在時域先進行奇歐倒序，頻域輸出為正序

DIF2 FFT其輸入序列在時域是正序，而頻域輸出為奇偶分開的倒序。

代碼實踐好了，前面碼了這么多字，還是不夠直觀，為了更好說明前面的分治思想，這里放了個遞歸實現(xiàn)代碼測一下看看療效：

#include 《assert.h》

#include 《math.h》

#include 《stdio.h》

#include 《stdlib.h》

#define q 8 /* 2^q 點，256 */

#define N （1《《q） /* N點 FFT， iFFT */

typedef float real;

typedef struct{

real Re;

real Im;

} complex;

#ifndef PI

# define PI 3.14159265358979323846264338327950288

#endif

/*為了更好說明分治思想，這里采用遞歸實現(xiàn)，結(jié)束條件為N《=1*/

void fft（ complex *v， int n， complex *tmp ）

if（n》1） { /* N如小于1，直接返回*/

int k，m; complex z， w， *vo， *ve;

ve = tmp; vo = tmp+n/2;

for（k=0; k《n/2; k++） {

ve［k］ = v［2*k］;

vo［k］ = v［2*k+1］;

fft（ ve， n/2， v ）; /* FFT 偶數(shù)序列 v［］ */

fft（ vo， n/2， v ）; /* FFT 偶數(shù)序列 v［］ */

for（m=0; m《n/2; m++） {

w.Re = cos（2*PI*m/（double）n）;

w.Im = -sin（2*PI*m/（double）n）;

z.Re = w.Re*vo［m］.Re - w.Im*vo［m］.Im; /* Re（w*vo［m］） */

z.Im = w.Re*vo［m］.Im + w.Im*vo［m］.Re; /* Im（w*vo［m］） */

v［ m ］.Re = ve［m］.Re + z.Re;

v［ m ］.Im = ve［m］.Im + z.Im;

v［m+n/2］.Re = ve［m］.Re - z.Re;

v［m+n/2］.Im = ve［m］.Im - z.Im;

return;

/*為了更好說明分治思想，這里采用遞歸實現(xiàn)，結(jié)束條件為N《=1*/

void ifft（ complex *v， int n， complex *tmp ）

if（n》1） {

int k，m; complex z， w， *vo， *ve;

ve = tmp; vo = tmp+n/2;

for（k=0; k《n/2; k++） {

ve［k］ = v［2*k］;

vo［k］ = v［2*k+1］;

ifft（ ve， n/2， v ）; /* FFT 偶數(shù)序列 v［］ */

ifft（ vo， n/2， v ）; /* FFT 奇數(shù)序列 v［］ */

for（m=0; m《n/2; m++） {

w.Re = cos（2*PI*m/（double）n）;

w.Im = sin（2*PI*m/（double）n）;

z.Re = w.Re*vo［m］.Re - w.Im*vo［m］.Im; /* Re（w*vo［m］） */

z.Im = w.Re*vo［m］.Im + w.Im*vo［m］.Re; /* Im（w*vo［m］） */

v［ m ］.Re = ve［m］.Re + z.Re;

v［ m ］.Im = ve［m］.Im + z.Im;

v［m+n/2］.Re = ve［m］.Re - z.Re;

v［m+n/2］.Im = ve［m］.Im - z.Im;

return;

#define SAMPLE_RATE （10000.0f）

int main（void）

complex v［N］， scratch［N］;

float amp［N］;

int k;

/*模擬一個采樣系統(tǒng)，采樣率為10KHz，有兩個信號：500Hz/2kHz*/

for（k=0; k《N; k++） {

v［k］.Re = 1*sin（2*PI*500*k/SAMPLE_RATE）+0.5*sin（2*PI*2000*k/SAMPLE_RATE）;

v［k］.Im = 0;//實際信號處理時，虛部常為0

/*輸出模擬信號*/

for（int i=0;i《N;i++）

printf（“%f，”，v［i］.Re）;

printf（“

fft（ v， N， scratch ）;

for（ int i=0;i《N;i++）

printf（“%f，”，sqrt（v［i］.Re*v［i］.Re+v［i］.Im*v［i］.Im））;

printf（“

”）;

while（1）;

總結(jié)一下本文目的為了方便理解快速傅立葉的算法思想，如果需要將算法實際應(yīng)用到單片機或者DSP中，還需要做進一步的優(yōu)化，實際使用時，一般會將蝶形算子做成一個表，另外也會做定點優(yōu)化。對于ARM芯片而言，其CMSIS庫有現(xiàn)成的實現(xiàn)例子可以直接使用，對于TI系列DSP而言，也內(nèi)置了FFT代碼庫，可直接使用。
責(zé)任編輯:pj