通過區塊鏈，人類歷史上首次通過技術徹底、純粹地保障「私有財產神圣不可侵犯」。

讓人沉思，讓人興奮的一段話。

可在這背后的基礎技術「密碼學」是如何工作，以及保障數字資產的安全呢？無論你是愛好者亦或投資客，應該需要多少了解背后的原理，免得誤解，輕則鬧笑話，重則損失資產。因為我們總會聽到一些鬼扯的故事（幫我找回密碼吧！私鑰發到群里了誒！），皆是由于對錢包本質的不了解。

本文僅談論錢包原型涉及的相關密碼學，不包含 keystore，助記詞，轉賬交易等。

錢包如何生成

這是以太坊黃皮書關于錢包（私鑰、公鑰、地址）的描述，僅僅 2 行文字。主要講解私鑰通過 ECDSA（橢圓曲線簽名算法）推導出公鑰，繼而經過 Keccak 單向散列函數推導出地址。

分解為 3 個步驟：

1. 創建隨機私鑰 （64 位 16 進制字符 / 256 比特 / 32 字節）

2. 從私鑰推導出公鑰 （128 位 16 進制字符 / 512 比特 / 64 字節）

3. 從公鑰推導出地址 （40 位 16 進制字符 / 160 比特 / 20 字節）

這是我從 ethereumjs/keythereum 中剝離出來的 JavaScript 代碼，關于黃皮書上的公式的具體實現，僅僅 6 行代碼。

這是一件很奇妙的事情，2 行文字，6 行代碼承載著億萬級別的資產，但往往越簡單，越奧妙。以上的 6 行代碼，就已經囊括密碼學中大多數技術，比如隨機數生成器、非對稱加密，單向散列函數等。以下我會為大家解剖這 6 行代碼，逐一介紹背后相關的密碼學知識。

隨機數

隨機數用于生成私鑰，若隨機數可以被預測或重現，則私鑰就會立刻形同虛設。所以保證隨機數擁有下列三項特征，至關重要：

隨機性：不存在統計學偏差，完全雜亂的數列

不可預測性：不能從過去的數列推測下一個出現的數

不可重現性：除非將數列保存下來，否則不能重現相同的數列

軟件本身是無法生成具有不可重現性的隨機數，因為運行軟件的計算機本身僅具備有限的內部狀態。所以通過確定性的代碼，在周期足夠長的情況下，必然會出現相同的隨機數。因此要生成具備不可重現性的隨機數，需要從不確定的物理現象中獲取信息，比如周圍溫度、環境噪音、鼠標移動，鍵盤輸入間隔等。

在 Linux 內核中維護了一個熵池用來收集來自設備驅動程序和其它來源的環境噪音。熵（entropy）是描述系統混亂無序程度的物理量，一個系統的熵越大則說明該系統的有序性越差，即不確定性越大。

所以在選擇生成私鑰的隨機數方法時，需要選擇滿足密碼學強度的隨機數方法，比如 Node 中的 crypto.randomBytes。當你調用 crypto.randomBytes（32） 方法時，它會等待熵池搜集足夠的信息后，返回 64 位的隨機數，即私鑰。

另外，在以太坊中想要獲得隨機數是一件不容易的事情，因為礦工需要得到同樣的結果，并經過驗證提交到區塊鏈上。但如果 EVM 存在 random opcode，礦工會生成不一致隨機數，無法達成共識。

目前社區也提出相應的方案，Mist 的作者 Alex van de Sande 提出使用 blockhashes 生成隨機數，但由于礦工擁有操縱區塊數據的能力，如果有能力且愿意放棄 5 個區塊的獎勵，理論上可以間接影響隨機數，所以不是完全足夠安全可靠。

為了解決礦工有可能作惡的問題，國內社區提出 RANDAO： A DAO working as RNG of Ethereum 項目，構建一個人人可以參與的 DAO，通過經濟激勵，由所有參與者共同決定一個隨機數。在 RANDAO 的基礎上，Vitalik Buterin 也提出 RANDAO++ 方案，感興趣可以看看。

非對稱加密

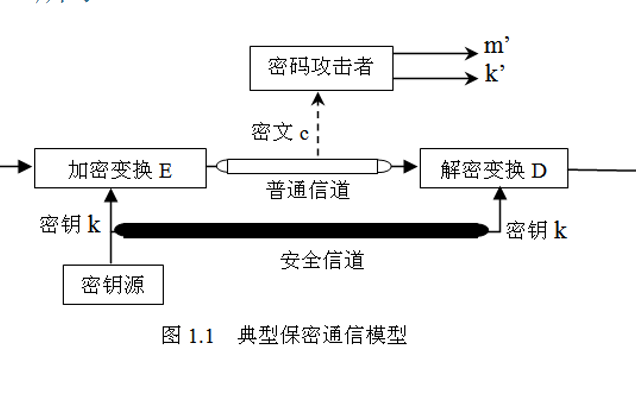
在對稱密碼中，由于加密和解密的密鑰相同，所以必須向接收者配送密鑰用于解密。但發送密鑰過程中，竊聽者可以竊取密鑰解密，不發送密鑰吧，接收者無法解密，密鑰必須發送，但又不能發送，這問題稱為密鑰配送問題。一般采取事先共享密鑰、密鑰分配中心、Diffie-Hellman 密鑰交換等方案來解決，但直到非對稱加密方案的出現，無需向接收者配送解密密鑰，密鑰配送問題才完美解決。

在非對稱加密中，將密鑰分為加密密鑰和解密密鑰，也就是我們常說的公鑰和私鑰。公鑰和私鑰一一對應，由公鑰加密的密文，必須使用公鑰配對的私鑰才可以解密。

看似有點復雜，我們祭出密碼學的男女主角 Alice 和 Bob，來通俗地梳理一下：

發送者： Bob，接收者：Alice，竊聽者：Eve

1. Alice 生成密鑰對（私鑰和公鑰），私鑰由 Alice 自身妥善保管

2. Alice 將自己的公鑰發送給 Bob，即使被 Eve 竊取也沒關系

3. Bob 使用 Alice 的公鑰對消息加密，發送給 Alice

4. 密文可能被 Eve 竊取，但他無法使用公鑰解密

5. Alice 使用自己的私鑰解密密文

當我們調用 secp256k1.publicKeyCreate 獲得公鑰時，實際使用的是非對稱加密中的橢圓曲線算法。通過該算法可以從私鑰推導出公鑰，這是一個不可逆的過程：K = k * G。給出常數點 G 時，使用已知私鑰 k 求公鑰 K 的問題并不困難，但反過來，已知公鑰 K 求私鑰 k，則非常困難。這就是橢圓曲線算法上的離散對數問題，也是為什么你可以分享地址（或公鑰）給別人，但不能暴露自己的私鑰。

const publicKey = secp256k1.publicKeyCreate（privateKey， false）.slice（1）

// publicKey.toString（‘hex’）： 1e3f1532e3285b02.。.45d91a36a8d78cb6bef8

為了形象的表現橢圓曲線算法如何將私鑰推導出公鑰，我們將使用簡單的整數作為私鑰 k，找到公鑰 K = k * G，也就是 G 相加 k 次（數學原理一致）。在橢圓曲線中， 點的相加等同于從該點畫切線找到與曲線相交的另?點， 然后映射到 x 軸。下圖展示了從曲線上獲得 G、2G、4G、8G 的幾何操作。

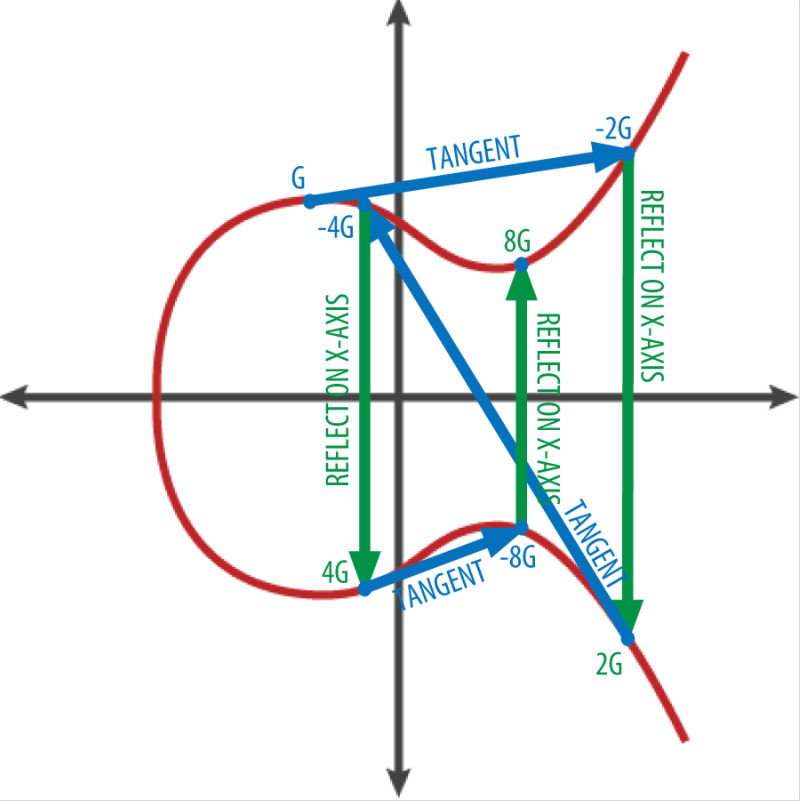
單向散列函數

單向散列函數 （one-way hash function） 有一個輸入和一個輸出，其中輸入稱為消息 （message） ，輸出稱為散列值 （hash value） 。散列值也稱為消息摘要 （message digest） 或者指紋 （fingerprint） 。單向散列函數可以根據消息的內容計算出散列值，而散列值就可以用來檢查消息的完整性。

單向散列函數擁有下列四項特征：

1. 根據任意長度的消息計算出固定長度的散列值

2. 能夠快速計算出散列值

3. 具備單向性

4. 消息不同散列值也不同

當我們調用 createKeccakHash（“keccak256”） 方法時，Keccak 使用海綿函數，對公鑰與初始的內部狀態做 XOR 運算得到 32 字節散列值，取其后 20 字節，轉成 40 位的 16 進制字符，即為地址。

在以太坊中還有許多地方應用了單向散列函數，例如：

1. 礦工需要不斷計算特定數據的散列值，當散列值滿足難度要求時，礦工便可以廣播該區塊，獲得獎勵。

2. 根據默克爾樹根哈希的值前后是否一致來判斷區塊中的交易是否被篡改

題外話，有一陣子我很好奇單向散列函數或哈希函數中的 ”Hash“ 代表什么意思呢？后來經過查詢得知， ”Hash“ 在古法語中的原意時「斧頭」，后來被引申為「剁碎」，正好形象的比喻單向散列函數，將消息剁碎，混合成固定長度的散列值。后來通過 Herbert Hellerman 的《Digital Computer System Principles》成為廣為流傳的術語。